Графические информационные модели - МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПРОВЕДЕНИЮ УРОКОВ В 9 КЛАССЕ

Планируемые образовательные результаты:

• предметные — представление о сущности и разнообразии графических информационных моделей;

• метапредметные — владение информационным моделированием как важным методом познания;

• личностные — представление о сферах применения информационного моделирования.

Решаемые учебные задачи:

1) обобщение и систематизация представлений учащихся о графических информационных моделях;

2) рассмотрение примеров использования графов как разновидности информационных моделей.

Основные понятия, рассматриваемые на уроке:

• схема;

• карта;

• чертеж;

• график;

• диаграмма;

• граф;

• сеть;

• дерево.

Средства ИКТ, используемые на уроке:

• персональный компьютер (ПК) учителя, мультимедийный проектор, экран;

• ПК учащихся.

Электронное приложение к учебнику:

• презентация “Графические информационные модели”.

Единая коллекция цифровых образовательных ресурсов:

1) интерактивный задачник, раздел “Графические модели” (119308);

2) инструмент разработки и анализа родословных “Живая Родословная” (145555).

Особенности изложения содержания темы урока

В начале урока осуществляется:

1) визуальная проверка выполнения домашнего задания в РТ;

2) рассмотрение заданий, вызвавших затруднения при выполнении домашнего задания;

3) демонстрация нескольких ученических презентаций (при их наличии).

Урок строится на основе презентации “Графические модели” из электронного приложения к учебнику. Целесообразно организовать беседу учащихся, в ходе которой обобщить и систематизировать их представления о разнообразных графических моделях. Рассмотрение блока, касающегося многообразия графических информационных моделей, можно завершить работой во фронтальном режиме с интерактивным задачником (раздел “Графические модели”, режим “Практика”).

Основное внимание следует уделить понятию графа. Эта тема поддерживается большим количеством задач в рабочей тетради.

В процессе рассмотрения материала урока выполнить № 34 (1, 2), 36, 39, 41, 44 в РТ, № 6, 10 и задание № 11 к § 1.3.

В практической части урока можно познакомить учащихся с инструментом разработки и анализа родословных “Живая Родословная”.

Домашнее задание

§ 1.3; вопросы и задания № 1-5, 7-9, 12 к параграфу; № 35, 37, 38, 40, 42 в РТ.

Дополнительное задание: № 34 (3, 4), 43 или 45 в РТ.

Указания, комментарии, ответы и решения

Задания в учебнике

№ 6. По условию задачи строим взвешенный граф:

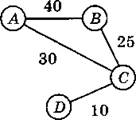
С учетом скорости движения велосипедиста по грунтовой дороге (20 км/ч) и по шоссе (30 км/ч) вычислим время (в часах), требуемое для преодоления расстояния между каждой парой населенных пунктов, соединенных дорогами.

По получившемуся взвешенному графу легко оценить минимально возможное время движения велосипедиста между любыми из имеющихся населенными пунктами.

№ 7. На первый взгляд это задание может показаться очень простым, но выполнить его будет достаточно сложно. Необходимо проанализировать текст, вычленить из него объекты (вершины графа) и зафиксировать связи между ними (ребра графа), изобразить соответствующий граф.

Например, по сказке “Царевна-лягушка” можно построить следующую семантическую сеть:

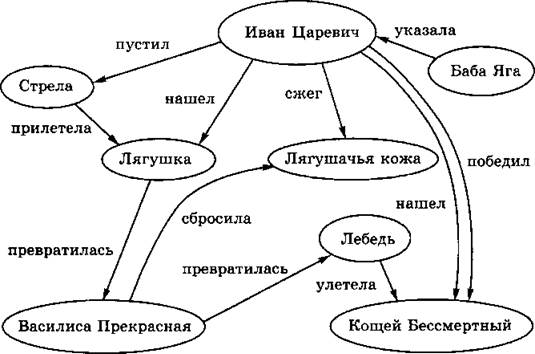
Возможно, учителю будет полезно познакомиться с сайтом о развитии навыков функционального чтения (https://sites.google.com/site/kursusfunctreading/7-aktivnoe-ctenie-priemy-vizualizacii/semanticeskie-grafy) и увидеть примеры ученических работ.

Ученики могут предложить различные варианты семантической сети по сказке “Колобок”. На базе этого задания можно организовать групповую работу с обязательным представлением и обсуждением полученных результатов.

№ 9. На первом месте в числе может стоять любая из четырех имеющихся цифр (четыре варианта), на втором месте — любая, кроме той, что уже использовали (три варианта), на третьем — любая из двух, не использовавшихся ранее. Итого: 4 ∙ 3 ∙ 2 = 24 (числа).

№ 10. В десятичной системе счисления для записи чисел используются 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. На первом месте в трехзначном числе может стоять любая из девяти цифр (0 на первом месте стоять не может), на втором — любая из девяти оставшихся (с учетом нуля), на третьем — любая из восьми, отличная от стоящих на первом и втором местах. Всего 9-9-8 вариантов.

№ 11. Всего 16 цепочек.

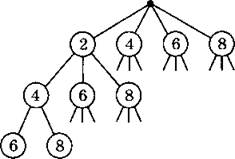
№ 12. Построим дерево игры:

При безошибочной игре выигрывает первый игрок. Своим первым ходом он должен взять один камень. В куче останется пять камней. Какой бы ход ни сделал второй игрок, в куче останется 4, 3 или 2 камня. Это позволяет первому игроку своим вторым ходом оставить в куче ровно один камень, его и должен будет забрать своим вторым ходом второй игрок.

Задания в рабочей тетради

№ 34

№	Количество вершин	Количество ребер	Количество циклов
1	4	6	5
2	6	8	5
3	8	12	28
4	5	10	17

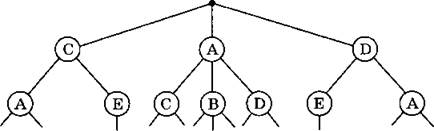
При подсчете циклов сложности могут возникнуть с графами 3 и 4. Рассмотрим их более подробно.

Подсчитать циклы в графе 3 помогут рисунки:

Подсчитать циклы в графе 4 помогут рисунки:

№ 37. 18 чисел: 102, 103, 120, 123, 130, 132, 201, 203, 210, 213, 230, 231, 301, 302, 310, 312, 320, 321.

№ 38. 13 цепочек.

№ 39

Пары населенных пунктов	Кратчайшие расстояния между пунктами	Пара самых удаленных друг от друга пунктов
АБ	5	АВ
АВ	15
АГ	8
БВ	10
БГ	3
ВГ	7

№ 40

Пары населенных пунктов	Кратчайшие расстояния между пунктами
АБ	х ≤ 7
АВ	х + 2 ≤ 7
АГ	х + 3 или 7
БВ	2
БГ	3
ВГ	5

Ответ: При х ≤ 5.

№ 41. 4 различных маршрута. Самый короткий маршрут: АБВЕ = 19 км. Для посещения всех торговых точек нужно выбрать маршрут АБГДВЕ.

№ 42. 33 балла (Старт-Б-А-В-Б-Г-В-Финиш).

№ 43. Метки, стоящие рядом с каждой вершиной, и есть искомые расстояния от А до соответствующей вершины.

№ 44. На дереве команде 1 (+1) будут соответствовать ребра, идущие влево; ребра, идущие вправо, будут соответствовать команде 2 (х2).

С помощью графа представлено 7 программ. Это ровно половина программ, решающих поставленную задачу.

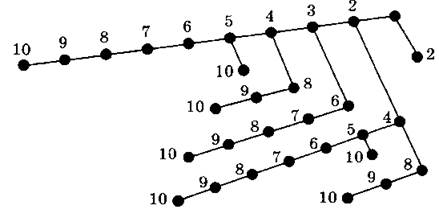
Ответ: 14 программ.

№ 45. Сложение и вычитание имеют одинаковый приоритет. Поэтому один и тот же результат будет получаться, например, при выполнении программ 1122 и 1221. Действительно, если применить эти программы к некому исходному числу х, то мы получим: х + 4 + 4 – 3 - 3 = х+ 2 и x – 3 + 4 + 4 - 3 = x + 2. Следовательно, разные результаты получатся в программах, содержащих:

1) четыре команды “прибавить 4”;

2) три команды “прибавить 4” и одну команду “вычесть 3”;

3) две команды “прибавить 4” и две команды “вычесть 3”;

4) одну команду “прибавить 4” и три команды “вычесть 3”;

5) четыре команды “вычесть 3”.

Ответ: 5 разных чисел.

№ 46. См. решение № 12 к § 1.3.