Алгоритмы - Разработка и применение - 2016 год
Рандомизация принципа разделяй и властвуй: нахождение медианы и быстрая сортировка - Рандомизированные алгоритмы
Применение парадигмы “разделяй и властвуй” при разработке алгоритмов уже рассматривалось в одной из предыдущих глав. Принцип “разделяй и властвуй” хорошо работает в сочетании с рандомизацией; чтобы доказать это, мы приведем алгоритмы “разделяй и властвуй” для двух фундаментальных задач: вычисления медианы n чисел и сортировки. В каждом случае шаг “разделяй” выполняется с применением рандомизации, после чего ожидаемые значения случайных переменных используются для анализа времени, затраченного на рекурсивные вызовы.
Задача: нахождение медианы
Предположим, имеется множество из n чисел S = {а1, a2, ... an}. Медианой этого множества называется число, которое займет среднюю позицию в результате сортировки. При четном nпоявляется неприятное техническое осложнение, так как “средней позиции” не существует, поэтому формальное определение выглядит так: медиана S = {а1, а2, ..., an} равна k-му по величине элементу S, где k = (n + 1)/2 при нечетном n и k = n/2 при четном n. В дальнейшем для простоты будем считать, что все числа различны. Без этого предположения формулировка задачи усложняется, но ничего принципиально нового в решении не появляется.
Очевидно, медиана легко вычисляется за время O(n log n), если числа будут предварительно отсортированы. Но если задуматься, становится совершенно не очевидно, почему для задачи нахождения медианы необходима сортировка, — как и то, почему для нее необходимо время Ω(n log n). Мы покажем, что простой рандомизированный алгоритм, основанный на принципе “разделяй и властвуй”, — ожидаемое время выполнения O(n).
Разработка алгоритма
Обобщенный алгоритм с разделителями
Первым ключевым шагом к ожидаемому линейному времени выполнения станет переход от нахождения медианы к более общей задаче выбора. Для заданного множества S, состоящего из nчисел, и числа k от 1 до n рассмотрим функцию Select(S, k), которая возвращает k-й по величине элемент S. Частными случаями Select являются задачи нахождения медианы S через Select(S, n/2) или Select(S, (n + 1)/2); она также включает более простые задачи нахождения минимума (Select(S, 1)) и максимума (Select(S, n)). Требуется разработать алгоритм, реализующий Select с выполнением за ожидаемое время O(n).
Базовая структура алгоритма, реализующего Select, выглядит так.
Мы берем элемент ai ∈ S — “разделитель” — и формируем множества ![]() Затем мы определяем, какое из множеств S- или S+ — содержит k-й по величине элемент, и выполняем итерацию только по нему. Не уточняя, как мы планируем выбирать разделитель, приведем более конкретное описание того, как формируются множества и проводятся итерации.
Затем мы определяем, какое из множеств S- или S+ — содержит k-й по величине элемент, и выполняем итерацию только по нему. Не уточняя, как мы планируем выбирать разделитель, приведем более конкретное описание того, как формируются множества и проводятся итерации.

Заметим, что алгоритм всегда рекурсивно вызывается для строго меньшего множества, поэтому он должен завершиться. Также заметим, что если |S| = 1, то и k = 1; единственный элемент Sбудет возвращен алгоритмом. Наконец, из выбора рекурсивного вызова по индукции очевидно, что правильный ответ также будет возвращен при |S| > 1. Мы приходим к следующему выводу:
(13.17) Независимо от выбора разделителя описанный алгоритм возвращает k-й по величине элемент S.
Выбор хорошего разделителя
Теперь разберемся, как время выполнения Select зависит от способа выполнения разделителя. Если предположить, что разделитель выбирается за линейное время, то остаток алгоритма выполняется за линейное время плюс время рекурсивного вызова. Но как выбор разделителя влияет на время выполнения рекурсивного вызова? На самом деле важно, что разделитель значительно сокращает размер рассматриваемого множества, чтобы нам не приходилось многократно перебирать большие множества чисел. Хороший выбор разделителя должен порождать множества S- и S+ приблизительно равного размера. Например, если бы мы могли всегда выбирать медиану в качестве разделителя, то для времени выполнения можно было бы установить линейную границу. Пусть cn — время выполнения Select, не считая времени рекурсивного вызова. Тогда, при выборе медиан в качестве разделителей, время выполнения T(n) будет ограничиваться рекуррентным отношением T(n) ≤ T(n/2) + cn. Это рекуррентное отношение уже встречалось нам в начале главы 5, где было показано, что у него имеется решение T(n) = O(n).
Конечно, стремление использовать медиану в качестве разделителя выглядит своего рода “порочным кругом” — ведь именно медиану мы и хотели вычислить! Но на самом деле понятно, что хорошим разделителем может послужить любой “более или менее центральный” элемент: если бы мы могли выбрать медиану так, чтобы в множестве присутствовали как минимум εnэлементов, больших и меньших аi для любой фиксированной константы ε > 0, то размер множеств в рекурсивном вызове каждый раз будет уменьшаться как минимум с множителем (1 - ε). Таким образом, время выполнения T(n) будет ограничиваться рекуррентным отношением T(n) ≤ T((1 - ε)n) + cn. Здесь можно воспользоваться тем же аргументом, который показал, что предыдущее рекуррентное отношение имеет решение T(n) = O(n): развертывая это рекуррентное отношение для любого ε > 0, получаем
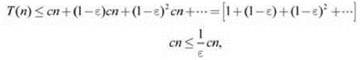
так как мы имеем дело со сходящейся геометрической прогрессией.
Единственное, чего следует действительно остерегаться, — это разделитель, “смещенный от центра”. Например, если всегда выбирать в качестве разделителя минимальный элемент, то множество, используемое для рекурсивного вызова, может содержать всего на один элемент меньше предыдущего. В этом случае время выполнения T(n) будет ограничено рекуррентным отношением T(n) ≤ T(n - 1) + cn. При раскрутке этого рекуррентного отношения возникает проблема:
![]()
Случайные разделители
Выбор разделителя “из центра” (в только что определенном смысле) безусловно напоминает исходную задачу выбора медианы; но на самом деле все не так плохо, так как подойдет любой разделитель “из центра”.
По этой причине еще не определенный шаг выбора разделителя будет реализован по следующему простому правилу:
Выбрать разделитель аi ∈ S случайно с равномерным распределением.
Правило основано на очень естественном представлении: так как достаточно большая часть элементов находится “недалеко от центра”, случайный выбор с большой вероятностью обеспечит хорошее разбиение.
Эта идея заложена в основу анализа времени выполнения со случайным разделителем; ожидается, что размер рассматриваемого множества будет уменьшаться с фиксированным постоянным коэффициентом при каждой итерации, поэтому мы должны получить сходящуюся прогрессию, а следовательно, линейную границу, как в предыдущем случае.
Анализ алгоритма
Будем считать, что алгоритм находится в фазе j, когда размер рассматриваемого множества не превышает ![]() но при этом он больше
но при этом он больше ![]() Попробуем найти границу для ожидаемого времени, проводимого алгоритмом в фазе j. В заданной итерации алгоритма элемент рассматриваемого множества называется центральным, если по крайней мере четверть элементов меньше и по крайней мере четверть элементов больше него.
Попробуем найти границу для ожидаемого времени, проводимого алгоритмом в фазе j. В заданной итерации алгоритма элемент рассматриваемого множества называется центральным, если по крайней мере четверть элементов меньше и по крайней мере четверть элементов больше него.
Теперь заметим, что если в качестве разделителя выбирается центральный элемент, то по крайней мере четверть множества будет отброшена, множество уменьшится с коэффициентом 3/4 или лучше, и текущая фаза подойдет к концу. Кроме того, к категории центральных относится половина всех элементов в множестве, поэтому вероятность того, что случайный выбор разделителя даст центральный элемент, равна 1/2. Следовательно, из простой границы времени ожидания (13.7) ожидаемое количество итераций перед обнаружением центрального элемента равно 2; а значит, ожидаемое количество итераций, проведенных в фазе j, для любого j не превышает 2.
Собственно, это все, что необходимо для анализа. Пусть X — случайная переменная, равная количеству шагов, предпринятых алгоритмом. Ее можно записать в виде суммы X = X0 + X1 + X2 + ..., где Xj — ожидаемое количество шагов, проведенных алгоритмом в фазе j. Когда алгоритм находится в фазе j, размер множества не превышает ![]() поэтому количество шагов, необходимых для одной итерации в фазе j, не превышает
поэтому количество шагов, необходимых для одной итерации в фазе j, не превышает ![]() для некоторой константы с. Мы только что обосновали, что ожидаемое количество итераций, проводимых в фазе j, не превышает 2, а следовательно,
для некоторой константы с. Мы только что обосновали, что ожидаемое количество итераций, проводимых в фазе j, не превышает 2, а следовательно, ![]() Это позволяет ограничить общее ожидаемое время выполнения с использованием линейности ожидания:
Это позволяет ограничить общее ожидаемое время выполнения с использованием линейности ожидания:
![]()
так как сумма ![]() представляет собой сходящуюся геометрическую прогрессию. Приходим к следующему результату:
представляет собой сходящуюся геометрическую прогрессию. Приходим к следующему результату:
(13.18) Ожидаемое время выполнения Select(n, k) равно O(n).
Второй пример: быстрая сортировка
Рандомизированный метод “разделяй и властвуй”, который использовался для нахождения медианы, также заложен в основу алгоритма быстрой сортировки. Как и прежде, мы выбираем разделитель для входного множества S и разбиваем S по элементам со значениями ниже и выше разделителя. Различие в том, что вместо поиска медианы только с одной стороны от разделителя мы рекурсивно сортируем обе стороны и соединяем два отсортированных фрагмента (с промежуточным разделителем) для получения общего результата. Кроме того, необходимо явно включить базовый случай для рекурсивного кода: рекурсия используется только для множеств с размером 4 и более. Полное описание алгоритма быстрой сортировки приведено ниже.

Как и в случае с нахождением медианы, время выполнения этого метода в худшем случае не впечатляет. Если всегда выбирать в качестве разделителя наименьший элемент, но время выполнения T(n) для n-элементных множеств определяется уже знакомым рекуррентным отношением: Т(n) ≤ Т(n - 1) + сn, так что в итоге приходим к границе T(n) = Ө(n2) (худшее время быстрой сортировки из всех возможных).
С другой стороны, если при каждой итерации в качестве разделителя выбирается медиана каждого множества, то получается рекуррентное отношение T(n) ≤ 2T(n/2) + cn, часто встречавшееся при анализе алгоритмов “разделяй и властвуй” главы 5; время выполнения в этом случае составляет O(n log n).
Сейчас нас интересует ожидаемое время выполнения; мы покажем, что оно может быть ограничено величиной O(n log n) — почти такой же, как в лучшем случае при выборе разделителей идеально по центру. Наш анализ быстрой сортировки достаточно близко воспроизводит анализ нахождения медианы. Как и в процедуре Select, использованной при поиске медианы, ключевую роль играет определение центрального разделителя — разделяющего множество так, чтобы каждая сторона содержала не менее четверти элементов. (Как упоминалось ранее, для анализа достаточно, чтобы каждая сторона содержала некоторую фиксированную часть элементов; четверть выбрана для удобства.) Идея заключается в том, что случайный выбор с большой вероятностью приведет к центральному разделителю, а центральные разделители работают эффективно. В случае сортировки центральный разделитель разбивает задачу на две существенно меньшие подзадачи.
Чтобы упростить формулировку, мы слегка изменим алгоритм так, чтобы он выдавал рекурсивные вызовы только при обнаружении центрального разделителя. По сути, измененный алгоритм отличается от Quicksort тем, что он отбрасывает “нецентральные” разделители и делает повторную попытку; Quicksort, напротив, выдает рекурсивные вызовы даже с нецентральным разделителем. Дело в том, что ожидаемое время выполнения измененного алгоритма очень просто анализируется по прямой аналогии с нашим анализом нахождения медианы. Похожий, хотя и более сложный анализ также можно провести и для исходной реализации Quicksort; мы этот анализ рассматривать не будем.

Рассмотрим подзадачу для некоторого множества S. Каждая итерация цикла Пока выбирает возможный разделитель а. и тратит время O(|S|) на разбиение множества и принятие решения о том, является ли а. центральным элементом. Ранее мы обосновали, что количество необходимых итераций до нахождения центрального разделителя не превышает 2. Таким образом, мы получаем следующее утверждение:
(13.19) Ожидаемое время выполнения алгоритма для множества S без учета времени рекурсивных вызовов составляет O(|“S|).
Алгоритм рекурсивно вызывается для нескольких подзадач, которые будут группироваться по размеру. Задача будет называться относящейся к типу j, если размер рассматриваемого множества не превышает ![]() но при этом больше
но при этом больше ![]() Согласно (13.19), ожидаемое время, потраченное на подзадачу типа j без учета рекурсивных вызовов, равно
Согласно (13.19), ожидаемое время, потраченное на подзадачу типа j без учета рекурсивных вызовов, равно ![]() Чтобы ограничить общее время выполнения, необходимо найти границу количества подзадач каждого типа j. Разбиение подзадачи типа j по центральному разделителю создает две подзадачи более высокого типа. Таким образом, подзадачи заданного типа j не пересекаются, и мы получаем границу для количества подзадач.
Чтобы ограничить общее время выполнения, необходимо найти границу количества подзадач каждого типа j. Разбиение подзадачи типа j по центральному разделителю создает две подзадачи более высокого типа. Таким образом, подзадачи заданного типа j не пересекаются, и мы получаем границу для количества подзадач.
(13.20) Количество подзадач типа j, созданных алгоритмом, не превышает ![]()
Всего существует не более ![]() подзадач типа j, и ожидаемое время, потраченное на каждую, равно
подзадач типа j, и ожидаемое время, потраченное на каждую, равно ![]() согласно (13.19). Тогда, вследствие линейности ожидания, ожидаемое время, потраченное на подзадачи типа j, составляет O(n). Количество разных типов ограничивается величиной
согласно (13.19). Тогда, вследствие линейности ожидания, ожидаемое время, потраченное на подзадачи типа j, составляет O(n). Количество разных типов ограничивается величиной ![]() которая и дает желаемую границу.
которая и дает желаемую границу.
(13.21) Ожидаемое время выполнения измененного алгоритма Quicksort равно O(n log n).
Мы рассмотрели измененную версию Quicksort для упрощения анализа. Что касается исходной реализации, интуиция подсказывает, что ожидаемое время выполнения у нее не хуже, чем у измененного алгоритма, так как принятие нецентральных разделителей немного помогает с сортировкой (хотя и не так, как при выборе центрального разделителя). Как упоминалось ранее, формализация этого интуитивного представления приводит к границе ожидаемого времени O(n log n) для исходного алгоритма Quicksort, но подробный анализ здесь не приводится.