Кратчайшие пути в графе - Жадные алгоритмы

Некоторые базовые алгоритмы графов основаны на жадных принципах. В этом разделе рассматривается жадный алгоритм для задачи поиска кратчайших путей, а в следующем разделе будет рассматриваться построение остовных деревьев минимальной стоимости.

Задача

Как вы уже знаете, графы часто используются для моделирования сетей, в которых происходит переход от одной точки к другой: например, дорог на транспортных развязках или каналов связи с промежуточными маршрутизаторами. В результате задача поиска кратчайшего пути между узлами в графе вошла в число базовых алгоритмических задач. Даны узлы u и v; какой из путей u-vявляется кратчайшим? Также можно запросить более подробную информацию: задан начальный узелs, как выглядят кратчайшие пути от s ко всем остальным узлам?

Формальная постановка задачи кратчайших путей выглядит так: имеется направленный граф G = (V, E) с обозначенным начальным узлом s. Предполагается, что в графе существует путь от s к любому другому узлу G. Каждому ребру е назначена длина l_е ≥ 0, которая обозначает время (или расстояние, или затраты), необходимое для перемещения по е. Для пути P длина P(обозначаемая l(P)) вычисляется как сумма длин всех ребер, входящих в P. Наша задача — определить кратчайший путь от s к каждому из других узлов графа. Следует упомянуть, что хотя задача сформулирована для направленного графа, случай ненаправленного графа обеспечивается простой заменой каждого ненаправленного ребра e = (u, v) длины l_e двумя направленными ребрами (u, v) и (v, u), каждое из которых имеет длину l_e.

Разработка алгоритма

В 1959 году Эдгар Дейкстра предложил очень простой жадный алгоритм для решения задачи нахождения кратчайшего пути с одним источником. Мы начнем с описания алгоритма, который просто находит длину кратчайшего пути от s к каждому из остальных узлов графа; после этого можно будет легко получить сами пути. Алгоритм хранит множество S вершин u, для которых было определено расстояние d(u) кратчайшего пути от s; это множество представляет “исследованную” часть графа. Изначально S = {s}, а d(s) = 0. Затем для каждого узла v ∈ V - Sопределяется кратчайший путь, который может быть построен перемещением по пути в исследованной части S к некоторому u ∈ S, за которым следует одно ребро (u, v). Далее рассматривается характеристика Алгоритм выбирает узел v ∈ V - S, для которого эта величина минимальна, добавляет v в S и определяет d(v) как значение d'(v).

Получить пути s-u для расстояний, вычисленных алгоритмом Дейкстры, несложно. При добавлении каждого узла v во множество S просто сохраняется ребро (u, v), для которого было достигнуто значение Путь P_v неявно представляется этими ребрами: если (u, v) — ребро, сохраненное для v, то P_v — это (рекурсивно) путь P_u, за которым следует одно ребро (u, v). Иначе говоря, чтобы построить P_v, мы просто начинаем с v; переходим по ребру, сохраненному для v, в обратном направлении к u; затем переходим по ребру, сохраненному для u, в обратном направлении к его предшественнику, и т. д., пока не доберемся до s. Заметьте, что узел s должен быть достижим, так как обратный переход от v посещает узлы, добавлявшиеся в Sранее и ранее.

Чтобы лучше понять, как работает алгоритм, рассмотрите “снимок” его выполнения на рис. 4.7. На момент создания “снимка” были выполнены две итерации: первая добавила узел u, а вторая — узел v. В предстоящей итерации будет добавлен узел х, потому что с ним достигается наименьшее значение d'(x); благодаря ребру (u, х) имеем Обратите внимание: попытка добавить у или z в множество S в этой точке приведет к неправильным расстояниям кратчайших путей; в конечном итоге они будут добавлены из-за ребер от x.

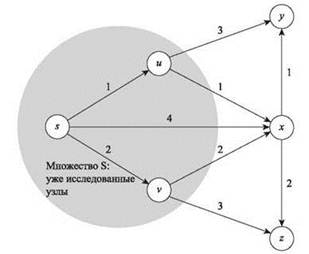
Рис. 4.7. Снимок выполнения алгоритма Дейкстры. Следующим узлом, добавляемым в множество S, будет узел x (из-за пути через u)

Анализ алгоритма

Из примера видно, что алгоритм Дейкстры работает правильно и избегает ловушек: добавление в множество S неправильного узла может привести к переоценке расстояния кратчайшего пути к этому узлу. Остается ответить на вопрос: всегда ли при добавлении алгоритмом Дейкстры узла v мы получаем истинное расстояние кратчайшего пути к v?

Ответ доказывает правильность алгоритма и то, что пути Р_u действительно являются кратчайшими. Алгоритм Дейкстры является жадным в том смысле, что он всегда строит кратчайший новый путь s-v, состоящий из пути из S, за которым следует одно ребро. Для доказательства правильности будет использована разновидность первого метода анализа: мы продемонстрируем, что это решение “идет впереди” всех остальных. Для этого мы покажем методом индукции, что каждый выбираемый им путь к узлу v будет короче любого другого пути к v.

(4.14) Рассмотрим множество S в любой точке выполнения алгоритма. Для каждого узла u ∈ S путь Р_u является кратчайшим путем s-u.

Обратите внимание: этот факт немедленно доказывает правильность алгоритма Дейкстры, так как его можно применить к моменту завершения алгоритма, когда S включает все узлы.

Доказательство. Для доказательства будет использоваться индукция по размеру S. Случай |S| = 1 тривиален: в этом состоянии S = {s} и d(s) = 0. Предположим, утверждение истинно для |S| = k при некотором значении k ≥ 1; теперь S увеличивается до размера k + 1 добавлением узла v. Пусть (u, v) — последнее ребро пути s-v P_v.

Согласно индукционной гипотезе, P_u является кратчайшим путем s-u для всех u ∈ S. Теперь возьмем любой другой путь s-v P; мы хотим показать, что он по крайней мере не короче P_v. Чтобы достичь узла v, путь P должен где-то выйти из множества S; пусть у — первый узел P, не входящий в S, и x ∈ S — узел, непосредственно предшествующий у.

Ситуация изображена на рис. 4.8, и суть доказательства очень проста: путь P не может быть короче P_v, потому что он уже был не короче P_v к моменту выхода из множества S. Действительно, в итерации k + 1 алгоритм Дейкстры уже должен был рассмотреть добавление узла у в множество S по ребру (x, у) и отклонить этот вариант в пользу добавления v. Это означает, что не существует пути от s к у через х, который был бы короче P_v. Но подпуть P до узла у является как раз таким путем, так что этот путь по крайней мере не короче P_v. А поскольку длины ребер неотрицательные, полный путь P по крайней мере не короче P_v.

Рис. 4.8. Кратчайший путь P_v и альтернативный путь s-v P через узел у

Это полное доказательство; также можно изложить аргумент из предыдущего абзаца с использованием следующих неравенств. Пусть P' — подпуть P от s до х. Так как х ∈ S, из индукционной гипотезы известно, что Р_х является кратчайшим путем s-x (с длиной d(x)), поэтому l(P') ≥ l(P_x) = d(x). Следовательно, подпуть P к узлу у имеет длину l(P') + l(x, у) ≥ d(x) + l(x, у) ≥ d'(y), и полный путь P по крайней мере не короче этого подпути. Наконец, раз алгоритм Дейкстры выбрал v на этой итерации, мы знаем, что d'(y) ≥ d'(v) = l(P_v). Объединение этих неравенств показывает, что l(P) ≥ l(P') + l(x, у) ≥ l(P_v). ■

Приведем пару замечаний относительно алгоритма Дейкстры и его анализа. Во-первых, алгоритм не всегда находит кратчайшие пути, если некоторые ребра имеют отрицательную длину. (А вы видите, где нарушается работа алгоритма?) Отрицательная длина ребер встречается во многих задачах нахождения кратчайшего пути, и в таких ситуациях требуется более сложный алгоритм, предложенный Беллманом и Фордом. Мы рассмотрим этот алгоритм, когда займемся темой динамического программирования.

Второе замечание заключается в том, что алгоритм Дейкстры в некотором смысле еще проще приведенного описания. Алгоритм Дейкстры в действительности является “непрерывной” версией алгоритма поиска в ширину для обхода графа; это можно пояснить физической аналогией. Допустим, ребра G образуют систему труб, заполненных водой и состыкованных в узлах; каждое ребро е обладает длиной l_е и фиксированным поперечным сечением. Теперь допустим, что в узле s падает капля воды, в результате чего от s начинает расходиться волна. Так как волна распространяется от s с постоянной скоростью, расширяющаяся сфера волнового фронта достигает узлов в порядке возрастания их расстояния от s. Интуиция подсказывает, что путь, по которому проходит фронт для достижения любого узла v, является кратчайшим (и это действительно так). Как нетрудно убедиться, именно этот путь v будет найден алгоритмом Дейкстры, а расширяющаяся волна доходит до узлов в том же порядке, в котором они обнаруживаются алгоритмом Дейкстры.

Реализация и время выполнения

Обсуждение алгоритма Дейкстры завершается анализом его времени выполнения. Для графа с n узлами цикл состоит из n - 1 итераций, так как каждая итерация добавляет в S новый узел v. С эффективностью выбора правильного узла v дело обстоит сложнее. Первая мысль — при каждой итерации рассмотреть новый узел v ∈ S, перебрать все ребра между S и v с вычислением минимума чтобы выбрать узел v с наименьшим значением. Для графа с m ребрами вычисление минимумов будет выполняться за время O(m), так что полученная реализация будет выполняться за время O(mn).

Правильный выбор структуры данных позволяет существенно улучшить результат. Прежде всего, значения минимумов следует явно хранить для каждого узла v ∈ V - S, чтобы не вычислять их заново при каждой итерации. Также эффективность можно повысить посредством хранения узлов V - S в приоритетной очереди с ключами d'(v). Приоритетные очереди рассматривались в главе 2; эти структуры данных предназначены для хранения множеств из n элементов с ключами. Приоритетная очередь обеспечивает эффективное выполнение вставки элементов, удаления элементов, изменения ключей и извлечения элементов с минимальным ключом. Нам понадобятся третья и четвертая из перечисленных операций; СhangeКеу и ExtractMin.

Как реализовать алгоритм Дейкстры с использованием приоритетной очереди? Узлы V помещаются в приоритетную очередь с ключом d'(v) для v ∈ V. Для выбора узла v, который должен быть добавлен в множество S, понадобится операция ExtractMin. Чтобы понять, как обновлять ключи, рассмотрим итерацию, в которой узел v добавляется в S; пусть w ∉ S — узел, остающийся в приоритетной очереди. Что нужно сделать для обновления значения d'(w)? Если (v, w) не является ребром, то делать ничего не нужно: множество ребер, рассматриваемых в минимуме в точности совпадает до и после добавления v в S. С другой стороны, если e' = (v, w) ∈ E, то новым значением ключа будет min(d'(w), d(v) + l_e,). Если d'(w) > d(v) + l_e, то нужно использовать операцию ChangeKey для соответствующего изменения ключа узла w. Операция ChangeKey может выполняться не более одного раза на ребро, при добавлении “хвоста” е' в S. Таким образом, мы получаем следующий результат.

(4.15) При использовании приоритетной очереди алгоритм Дейкстры для графа с n узлами и m ребрами может быть реализован с выполнением за время O(m) с добавлением времени nопераций ExtractMin и m операций ChangeKey.

При реализации приоритетной очереди на базе кучи (см. главу 2) все операции будут выполняться за время O(log n). Таким образом, общее время выполнения составит O(m log n).