Реализация алгоритма Крускала: структура Union-Find - Жадные алгоритмы

Одной из основных задач графов является поиск множества связных компонент. В главе 3 рассматривались алгоритмы с линейным временем, использующие поиск BFS и DFS для нахождения компонент связности графа.

В этом разделе будет рассмотрена ситуация, в которой граф развивается посредством добавления ребер. Другими словами, граф имеет фиксированный набор узлов, но со временем между некоторыми парами узлов появляются новые ребра. Требуется обеспечить хранение множества компонент связности такого графа в процессе эволюции. При добавлении в граф нового ребра было бы нежелательно заново вычислять компоненты связности. Вместо этого мы воспользуемся структурой данных, называемой структуройUnion-Find; эта структура позволяет хранить информацию компонент с возможностью быстрого поиска и обновления.

Именно такая структура данных необходима для эффективной реализации алгоритма Крускала. При рассмотрении каждого ребра e = (v, w) необходимо эффективно идентифицировать компоненты связности, содержащие v и w. Если эти компоненты различны, то пути между v и w не существует и ребро e следует включить; но если компоненты совпадают, то путь v-wсуществует на ранее включенных ребрах, поэтому ребро e опускается. При включении e структура данных также должна обеспечивать эффективное слияние компонент v и w в одну новую компоненту.

Задача

Структура данных Union-Find обеспечивает хранение информации о непересекающихся множествах (например, компонентах графа) в следующем смысле. Для заданного узла и операция Find(u) возвращает имя множества, содержащего u. При помощи этой операции можно проверить, принадлежат ли два узла u и v к одному множеству, просто проверяя условие Find(u) = Find(v). Структура данных также реализует операцию Union(A, B), которая берет два множества A и B и сливает их в одно множество.

Эти операции могут использоваться для хранения информации о компонентах эволюционирующего графа G = (V, E) по мере добавления новых ребер. Множества представляют компоненты связности графа. Для узла и операция Find(u) возвращает имя компоненты, содержащей u. Чтобы добавить в граф ребро (u, v), мы сначала проверяем, принадлежат ли u и v одной компоненте связности (условие Find(u) = Find(v)). Если они не принадлежат одной компоненте, то операция Union(Find(u), Find(v)) используется для слияния двух компонент. Важно заметить, что структура Union-Find может использоваться только для управления компонентами графа при добавлении ребер: она не предназначена для обработки удаления ребер, которое может привести к “разделению” одной компоненты надвое.

Итак, структура Union-Find будет поддерживать три операции.

♦ MakeUnionFind(S) для множества S возвращает структуру Union-Find. Например, эта структура соответствует набору компонент связности графа без ребер. Мы постараемся реализовать MakeUnionFind за время O(n), где n = |S|.

♦ Для элемента u ∈ S операция Find(u) возвращает имя множества, содержащего и. Нашей целью будет реализация Find(u) за время O(log n). Некоторые реализации, которые будут упомянуты в тексте, позволяют выполнить эту операцию за время O(1).

♦ Для двух множеств A и B операция Union(A, B) изменяет структуру данных, объединяя множестваA и B в одно. Нашей целью будет реализация Union за время O(log n).

Стоит разобраться, что же подразумевается под именем множества — например, возвращаемого операцией Find. Имена множеств определяются достаточно гибко; они просто должны быть непротиворечивыми в том отношении, что Find(v) и Find(w) должны возвращать одно имя, если v и w принадлежат одному множеству, и разные имена в противном случае. В наших реализациях имя каждого множества будет определяться одним из содержащихся в нем элементов.

Простая структура данных для структуры Union-Find

Возможно, самым простым вариантом реализации структуры данных Union-Find является массив Component, в котором хранится имя множества, содержащего каждый элемент. Пусть S — множество, состоящее из n элементов {1, ..., n}. Мы создаем массив Component размера n, в каждом элементе которого Component[s] хранится имя множества, содержащего s. Чтобы реализовать операцию MakeUnionFind(S), мы создаем массив и инициализируем его элементы Component [s] = s для всех s ∈ S. Эта реализация упрощает Find(v): все сводится к простой выборке по ключу, занимающей время O(1). Однако операция Union(A, B) для двух множеств A и B может занимать время до 0(n) из-за необходимости обновления значений Component[s] для всех элементов множеств A и B.

Чтобы улучшить эту границу, мы проведем несколько простых оптимизаций. Во-первых, будет полезно явно хранить список элементов каждого множества, чтобы для нахождения обновляемых элементов не пришлось просматривать весь массив. Кроме того, можно сэкономить немного времени, выбирая в качестве имени объединения имя одного из исходных множеств, скажем A: в этом случае достаточно обновить значения Component[s] для s ∈ B, но не для любых s ∈ A. Конечно, при большом множестве B выигрыш от этой идеи будет невелик, поэтому мы добавляем еще одну оптимизацию: для большого множества B будет сохраняться его имя, а значения Component[s] будут изменяться для s ∈ A. В более общей формулировке хранится дополнительный массив size размера n, где size[A] содержит размер множества A, а при выполнении операции Union(A, B) для объединения используется имя большего множества. Такой подход сокращает количество элементов, для которых требуется обновить значение Component.

Даже с такими оптимизациями операция Union в худшем случае выполняется за время O(n): это происходит при объединении двух больших множеств A и B, содержащих одинаковые доли всех элементов. Тем не менее подобные плохие случаи не могут встречаться очень часто, поскольку итоговое множество A U B имеет еще больший размер. Как точнее сформулировать это утверждение? Вместо того чтобы ограничивать время выполнения одной операции Union для худшего случая, мы можем ограничить общее (или среднее) время выполнения серии из к операций Union.

(4.23) Имеется реализация структуры данных Union-Find на базе массива для некоторого множества S размера n; за объединением сохраняется имя большего множества. Операция Findвыполняется за время O(1), MakeUnionFind(S) — за время O(n), а любая последовательность из к операций Union выполняется за время не более O(k log k).

Доказательство. Истинность утверждений относительно операций MakeUnionFind и Find очевидна. Теперь рассмотрим серию из k операций Union. Единственной частью операции Union, которая выполняется за время, большее O(1), является обновление массива Component. Вместо того чтобы ограничивать время одной операции Union, мы ограничим общее время, потраченное на обновление Component[v] для элемента v в серии из k операций.

Вспомните, что структура данных изначально находится в состоянии, при котором все п элементов находятся в отдельных множествах. В одной операции Union может быть задействовано не более двух исходных одноэлементных множеств, поэтому после любой последовательности из k операций Union все, кроме максимум 2k элементов S, останутся неизменными. Теперь возьмем конкретный элемент v. Так как множество v участвует в серии операций Union, его размер увеличивается. Может оказаться, что одни объединения изменяют значение Component[v], а другие нет. Но по нашему соглашению объединение использует имя большего множества, поэтому при каждом обновлении Component[v] размер множества, содержащего v, как минимум удваивается Размер множества v начинается с 1, а его максимально возможное значение равно 2k (как было указано выше, все, кроме максимум 2k элементов, не будут затронуты операциями Union). Это означает, что Component[v] в этом процессе обновляется не более log₂(2k) раз. Кроме того, в любых операциях Union будут задействованы не более 2k элементов, поэтому мы получаем границу O(k log k) для времени, проведенного за обновлением значений Component в серии из к операций Union. ■

Эта граница среднего времени выполнения серии из к операций достаточно хороша для многих приложений, включая реализацию алгоритма Крускала, мы попробуем ее улучшить, и сократить время худшего случая. Это будет сделано за счет повышения времени, необходимого для операции Find, до O(log n).

Усовершенствованная структура данных Union-Find

В структуре данных альтернативной реализации используются указатели. Каждый узел v ∈ S будет храниться в записи с указателем на имя множества, содержащего v. Как и прежде, мы будем использовать элементы множества S в качестве имен множеств, а каждое множество будет названо по имени одного из своих элементов. Для операции MakeUnionFind(S) запись каждого элемента v ∈ S инициализируется указателем, который указывает на себя (или определяется как null); это означает, что v находится в собственном множестве.

Рассмотрим операцию Union для двух множествA и B. Предположим, что имя, использованное для множества A, определяется узлом v ∈ A, тогда как множество B названо по имени узла u ∈ B. Идея заключается в том, чтобы объединенному множеству было присвоено имя и или v; допустим, в качестве имени выбирается v. Чтобы указать, что мы выполнили объединение двух множеств, а объединенному множеству присвоено имя v, мы просто обновляем указатель u так, чтобы он ссылался на v. Указатели на другие узлы множества B при этом не обновляются.

В результате для элементов w ∈ B, отличных от и, имя множества, которому они принадлежат, приходится вычислять переходом по цепочке указателей, которая сначала ведет к “старому имени” и, а потом по указателю от и — к “новому имени” v. Пример такого представления изображен на рис. 4.12. Например, два множества на рис. 4.12 могут представлять результат следующей серии операций Union: Union(w, u), Union(s, u), Union(l, v), Union(z, v), Union(i', x), Union(y, j), Union(x, j) и Union(u, v).

Структура данных с указателями реализует операцию Union за время O(1): требуется лишь обновить один указатель. Но операция Find уже не выполняется за постоянное время, потому что для перехода к текущему имени приходится отслеживать цепочку указателей с “историей” старых имен множества. Сколько времени может занимать операция Find(u)? Количество необходимых шагов в точности равно количеству изменений имени множества, содержащего узел и, то есть количеству обновлений позиции в массиве Component[u] в нашем представлении в виде массива. Оно может достигать O(n), если мы не проявим достаточной осторожности с выбором имен множеств. Для сокращения времени, необходимого для операции Find, мы воспользуемся уже знакомой оптимизацией: имя наибольшего множества сохраняется как имя объединения. Последовательность объединений, приведших к структуре на рис. 4.12, подчинялась этому правилу. Чтобы эффективно реализовать этот вариант, необходимо хранить с узлами дополнительное поле: размер соответствующего множества.

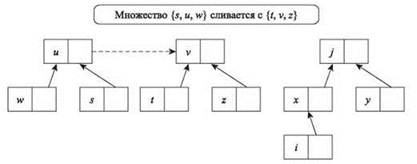
Рис. 4.12. Структура Union-Find с указателями. В данный момент структура содержит только два множества, названных по именам элементов v и j. Пунктирные стрелки от u к v представляют результат последней операции Union. Для обработки запроса Find мы перемещаемся по стрелкам, пока не доберемся до узла без исходящих стрелок. Например, для ответа на запрос Find(i) потребуется перейти по стрелке i к х, а затем от x к j

(4.24) Имеется описанная выше реализация структуры данных Union-Find с указателями для некоторого множества S размера п; за объединением сохраняется имя большего множества. Операция Union выполняется за время O(1), MakeUnionFind(S) — за время O(n), а операция Find — за время O(log n).

Доказательство. Истинность утверждений относительно операций Union и MakeUnionFind очевидна. Время выполнения Find(v) для узла v определяется количеством изменений имени множества, содержащего узел v, в процессе. По правилам за объединением сохраняется имя большего из объединяемых множеств, из чего следует, что при каждом изменении имени множества, содержащего узел v, размер этого множества по крайней мере удваивается. Поскольку множество, содержащее v, начинается с размера 1 и никогда не оказывается больше п, его размер может удваиваться не более log₂ n раз, а значит, имя может изменяться не более log₂ n раз. ■

Дальнейшие улучшения

Далее мы кратко рассмотрим естественную оптимизацию структуры данных Union-Find на базе указателей, приводящую к ускорению операций Find. Строго говоря, это улучшение не является необходимым для наших целей: для всех рассматриваемых применений структур данных Union-Find время 0(log п) на операцию достаточно хорошо в том смысле, что дальнейшее улучшение времени операций не преобразуется в улучшение общего времени выполнения алгоритмов, которые их используют. (Операции Union-Find не единственное вычислительное “узкое место” во времени выполнения этих алгоритмов.)

Чтобы понять, как работает улучшенная версия этой структуры данных, для начала рассмотрим “плохой” случай времени выполнения для структуры данных Union-Find на базе указателей. Сначала мы строим структуру, в которой одна из операций Find выполняется приблизительно за время log п. Для этого повторно выполняются операции Union для множеств равных размеров. Предположим, v — узел, для которого операция Find(v) выполняется за время log n. Теперь представьте, что Find(v) выполняется многократно, и каждое выполнение занимает время log n. Необходимость переходить по одному пути из log n указателей каждый раз для получения имени множества, содержащего v, оказывается лишней: после первого обращения Find(v) имя х множества, содержащего v, уже “известно”; также известно, что все остальные узлы, входящие в путь от v к текущему имени, тоже содержатся в множестве х. Итак, в улучшенной реализации путь, отслеживаемый для каждой операции Find, “сжимается”: все указатели в пути переводятся на текущее имя множества. Потери информации при этом не происходит, а последующие операции Find будут выполняться быстрее. Структура данных Union-Find и результат выполнения Find(v) с использованием сжатия изображены на рис. 4.13.

Рис. 4.13. (а) Пример структуры данных Union-Find; (b) результат выполнения операции Find(v) с использованием сжатия пути

Теперь рассмотрим время выполнения операций для такой реализации. Как и прежде, операция Union выполняется за время O(1), а операция MakeUnionFind(S) занимает время O(n) для создания структуры данных, представляющей множество размера n. Как изменилось время, необходимое для операции Find(v)? Некоторые операции Find по-прежнему занимают время до log n; для некоторых операций Find это время увеличилось, потому что после нахождения имени x множества, содержащего v, приходится возвращаться по той же цепочке указателей от v к x и переводить каждый указатель прямо на х. Но эта дополнительная работа в худшем случае удваивает необходимое время, а следовательно, не изменяет того факта, что операция Findвыполняется за максимальное время O(log n). Выигрыш от сжатия путей проявляется при последующих вызовах Find, а для его оценки можно воспользоваться тем же методом, который был применен в (4.23): ограничением общего времени серии из n операций Find (вместо худшего времени одной операции). И хотя мы не будем вдаваться в подробности, серия из n операций Findсо сжатием требует времени, чрезвычайно близкого к линейной зависимости от n; фактическая верхняя граница имеет вид O(nα(n)), где α(n) — очень медленно растущая функция n, называемая обратной функцией Аккермана. (В частности, a(n) < 4 для любых значений n, которые могут встретиться на практике.)

Реализация алгоритма Крускала

А теперь воспользуемся структурой данных Union-Find для реализации алгоритма Крускала. Сначала нужно отсортировать ребра по стоимости; эта операция выполняется за время O(m log m). Так как каждая пара узлов соединяется максимум одним ребром, m ≤ n², а следовательно, общее время выполнения также равно O(m log n).

После операции сортировки структура данных Union-Find используется для хранения информации о компонентах связности (V, T) при добавлении ребер. При рассмотрении каждого ребра e = (v, w) мы вычисляем Find(u) и Find(v) и проверяем результаты на равенство, чтобы узнать, принадлежат ли v и w разным компонентам. Если алгоритм решает включить ребро e в дерево T, операция Union(Find(u), Find(v)) объединяет две компоненты.

В процессе выполнения алгоритма Крускала выполняются не более 2m операций Find и n - 1 операций Union. Используя либо (4.23) для реализации Union-Find на базе массива, либо (4.24) для реализации с указателями, можно заключить, что общее время реализации равно O(m log n). (Хотя возможны и более эффективные реализации структуры Union-Find, они не улучшат время выполнения алгоритма Крускала, который содержит неизбежный фактор O(m log n) из-за исходной сортировки ребер по стоимости.)

Подведем итог:

(4.25) Алгоритм Крускала может быть реализован для графа с n узлами и m ребрами со временем выполнения O(m log n).