Алгоритмы - Разработка и применение - 2016 год
Поиск ближайшей пары точек - Разделяй и властвуй
В этом разделе описана другая задача, которая может быть решена алгоритмом рассматриваемого типа; но чтобы найти правильный способ “слияния” решений двух порождаемых подзадач, придется хорошенько подумать.
Задача
Формулировка задачи очень проста: для заданных n точек на плоскости найти пару точек, расположенных ближе друг к другу.
В начале 1970-х годов эту задачу рассматривали М. И. Шамос и Д. Хоуи в ходе проекта по поиску эффективных алгоритмов для базовых вычислительных примитивов для геометрических задач. Эти алгоритмы заложили основу зарождающейся в то время области вычислительной геометрии и проникли в такие области, как компьютерная графика, обработка изображений, географические информационные системы и молекулярное моделирование. И хотя задача нахождения ближайшей пары точек принадлежит к числу самых естественных алгоритмических задач в геометрии, найти для нее эффективный алгоритм оказывается на удивление сложно. Очевидно, существует решение O(n2) — вычислить расстояния между каждой парой точек и выбрать минимум; Шамос и Хоуи задались вопросом, существует ли алгоритм, который был бы асимптотически более быстрым, чем квадратичный. Прошло довольно много времени, прежде чем был получен ответ на этот вопрос. Приведенный ниже алгоритм O(n log n) по сути не отличается от найденного ими. Более того, когда мы вернемся к этой задаче в главе 13, то увидим, что время выполнения можно дополнительно улучшить до O(n) за счет применения рандомизации.
Разработка алгоритма
Начнем с определения некоторых обозначений. Имеется множество точек P = {p1, ..., pn}, в котором точка рi имеет координаты (xi, уj); для двух точек pi, pj ∈ р стандартное евклидово расстояние между ними будет обозначаться d(pi, pj). Наша цель — найти пару точек pi, pj, минимизирующую d(pi, pj).
Будем считать, что никакие две точки из P не имеют одинаковых значений координаты x или у. Такое предположение упрощает дальнейшее обсуждение; чтобы снять его, достаточно применить к точкам поворот, в результате которого предположение становится истинным, или слегка расширить описанный алгоритм.
Будет полезно рассмотреть одномерную версию этой задачи — она намного проще, а результаты показательны. Как найти ближайшую пару точек на прямой? Нужно сначала отсортировать точки за время O(n log n), а затем перебрать отсортированный список с вычислением расстояния от каждой точки до следующей. Понятно, что одно из этих расстояний должно быть минимальным.
На плоскости можно попытаться отсортировать точки по координате у (или х) и надеяться, что две ближайшие точки будут находиться поблизости в порядке сортировки. Но легко построить пример, в котором они будут находиться очень далеко, так что приспособить одномерное решение к двум измерениям не удастся.
Вместо этого будет применена стратегия в стиле “разделяй и властвуй”, использованная в сортировке слиянием: мы находим ближайшую пару среди точек в “левой половине” P и ближайшую пару среди точек в “правой половине” P, после чего эта информация используется для получения общего решения за линейное время. Если разработать алгоритм с такой структурой, то решение базового рекуррентного отношения из (5.1) обеспечит время выполнения O(n log n).
Сложности возникают в последней, “объединяющей” фазе алгоритма: ни один из рекурсивных вызовов не рассматривает расстояния между точкой из левой и точкой из правой половины; всего таких расстояний Q(n2), но мы должны найти наименьшее из них за время O(n) после завершения рекурсивных вызовов. Если это удастся сделать, то решение будет завершено: результатом становится меньшее из значений, вычисленных в ходе рекурсивных вызовов, и минимального расстояния между точками из левой и правой половин.
Подготовка рекурсии
Начнем с нескольких простых подготовительных операций. Было бы очень удобно, если бы каждый рекурсивный вызов для множества P' ⊆ P начинался с двух списков: списка P'x, в котором все точки P' отсортированы по возрастанию координаты х, и списка P'y, в котором все точки P' отсортированы по возрастанию координаты у. Для этого можно воспользоваться описанным ниже алгоритмом.
Еще перед началом рекурсии все точки P сортируются по координате х, а потом по координате у; так получаются списки Px и Py. С каждым элементом списка связана запись с информацией о позиции точки в обоих списках.
Первый уровень рекурсии работает так, как описано ниже; другие уровни работают полностью аналогично. Q определяется как множество точек в первых [n/2] позициях списка Px (“левая половина”), а R — как множество точек в других [n/2] позициях списка Px (“правая половина”); схема разбиения представлена на рис. 5.6. За один проход по Px и Py за время O(n) можно создать четыре списка: Qx с точками Q, отсортированными по возрастанию координаты х; Qy с точками Q, отсортированными по возрастанию координаты y; и два аналогичных списка Rx и Ry. Для каждого элемента каждого из этих списков также хранится его позиция в обоих исходных списках.
Затем рекурсивно определяется ближайшая пара точек в Q (с обращениями к спискам Ох и Qy). Предположим, q0* и q1*, (правильно) возвращены как ближайшая пара точек в Q. Аналогичным образом определяется ближайшая пара точек в R, обозначим их r0* и r1*.
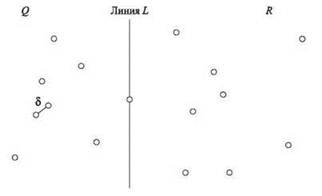
Рис. 5.6. Первый уровень рекурсии: множество точек P делится на равные половины Q и R по линии L и в каждой половине выполняется рекурсивный поиск ближайшей пары
Объединение решений
Общая схема “разделяй и властвуй” позволила нам дойти до этой точки, не углубляясь в структуру задачи нахождения ближайшей пары. Но при этом мы не решили исходную проблему: как использовать решения двух подзадач в “объединяющей” операции с линейным временем?
Введем обозначение δ для минимума из d(q0*, q1*) и d(r0*, r1*). Настоящий вопрос выглядит так: существуют ли точки q ∈ Q и r ∈ R, для которых d(q, r) < δ? Если нет, то ближайшая пара уже была найдена одним из предшествующих рекурсивных вызовов. Если же такие точки существуют, то ближайшие q и r образуют ближайшую пару в P.
Пусть х* обозначает координату х крайней правой точки в Q, а L — вертикальную линию, описываемую уравнением х = х*. Линия L “отделяет” Q от R. А теперь простой факт:
(5.8) Если существуют q ∈ Q и r ∈ R, для которых d(q, r) < δ, то каждая из точек q и r располагается в пределах расстояния δ от L.
Доказательство. Предположим, такие q и r существуют; обозначим q = (qx, qy) и r = (rx, ry). Из определения x* следует, что qx ≤ х* ≤ rx. Тогда
![]()
и
![]()
а это значит, что у каждой из точек q и r координата x находится в пределах δ от Х* — и следовательно, ее расстояние от линии L не превышает δ. ■
Итак, чтобы найти ближайшие точки q и r, поиск можно ограничить узкой полосой, содержащей только точки P, находящиеся в пределах δ от L. Допустим, это множество обозначается S ⊆ P, а Sy — список, состоящий из точек S, отсортированных по возрастанию координаты у. Один проход по списку Py строит Sy за время O(n).
В контексте множества S утверждение (5.8) переформулируется следующим образом.
(5.9) Существуют q ∈ Q и r ∈ R, для которых d(q, r) < δ в том и только в том случае, если существуют s, s' ∈ S, для которых d(s, s') < δ.
На этой стадии стоит заметить, что S может быть тождественно всему множеству P; в этом случае (5.8) и (5.9) вроде бы ничего не дают. Но это впечатление обманчиво, как показывает следующий удивительный факт.
(5.10) Если s, s' ∈ S обладают тем свойством, что d(s, s') < δ, то s и s' находятся на расстоянии не более 15 позиций друг от друга в отсортированном списке Sy.
Доказательство. Рассмотрим подмножество Z плоскости, состоящее из всех точек, удаленных от L на расстояние не более δ. Разделим Z на поля — квадраты со стороной δ/2. Один ряд Z будет состоять из четырех полей, горизонтальные стороны которых имеют одинаковые координаты у. Это множество полей изображено на рис. 5.7.
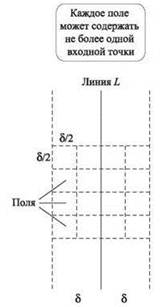
Рис. 5.7. Часть плоскости возле разделительной линии L — см. доказательство (5.10).
Допустим, две точки S лежат в одном поле. Так как все точки этого поля находятся по одну сторону от L, эти две точки либо обе принадлежат Q, либо обе принадлежат R. Но любые две точки в одном поле находятся на расстоянии не более δ ∙ √2/2 < δ, а это противоречит нашему определению 5 как минимального расстояния между любой парой точек Q или R. Следовательно, каждое поле содержит не более одной точки S.
Теперь допустим, что s, s' ∈ S обладают свойством d(s, s') < δ и находятся на расстоянии 16 и более позиций в Sy. Предположим без потери общности, что s имеет меньшую координату у. Так как поле может содержать не более одной точки, между 5 и s' лежат как минимум три ряда Z. Но любые две точки в Z, разделенные минимум тремя рядами, должны находиться на расстоянии минимум 3δ/2 — противоречие. ■
Заметим, что значение 15 можно сократить; но для нас сейчас важно то, что это абсолютная константа.
В свете (5.10) алгоритм можно завершить так: мы делаем один проход по Sy и для каждого s ∈ Sy вычисляем расстояние до каждой из следующих 15 точек в Sy. Из утверждения (5.10) следует, что при этом будет вычислено расстояние между каждой парой точек в S, находящихся на расстоянии менее δ друг от друга (если они есть). После этого можно сравнить наименьшее из этих расстояний с δ и выдать один из двух результатов: (i) ближайшую пару точек в S, если расстояние между ними меньше δ; или (ii) (обоснованное) заключение о том, что в S не существует пар точек, разделенных расстоянием не более δ. В случае (i) эта пара является ближайшей парой в P; в случае (ii) ближайшей парой в P будет ближайшая пара, найденная рекурсивными вызовами.
Обратите внимание на сходство этой процедуры с алгоритмом, отвергнутым в самом начале, в котором мы попытались ограничиться одним перебором P по координате у. Новый метод работает благодаря дополнительной информации (значение δ), полученной в результате рекурсивных вызовов, и специальной структуре множества S.
На этом описание “объединяющей” части алгоритма завершается, поскольку, согласно (5.9), мы определили, что минимальное расстояние между точкой из Q и точкой из R меньше δ, а это означает, что мы нашли ближайшую из таких пар.
Полное описание алгоритма и доказательство его правильности неявно содержатся в приведенном выше описании, но ради конкретности приведем краткие описания по обоим пунктам.
Краткое описание алгоритма
Ниже приводится высокоуровневое описание алгоритма с использованием введенных ранее обозначений.


Анализ алгоритма
Сначала мы докажем, что алгоритм выдает правильный ответ, используя факты, установленные в ходе его разработки.
(5.11) Алгоритм правильно находит ближайшую пару точек в P.
Доказательство. Как упоминалось ранее, все компоненты доказательства уже были представлены ранее, так что осталось лишь собрать их все воедино.
Для доказательства правильности будет использована индукция по размеру P; случай |P| ≤ 3 очевиден. Для заданного P ближайшая пара рекурсивных вызовов правильно вычисляется индукцией. Из (5.10) и (5.9) оставшаяся часть алгоритма правильно определяет, находится ли любая пара точек S на расстоянии менее δ, и если находится — возвращает такую пару с минимальным расстоянием. Теперь у ближайшей пары P либо обе точки принадлежат одному из множеств Q или R, либо они принадлежат разным множествам. В первом случае ближайшая пара находится рекурсивным вызовом; во втором она находится на расстоянии менее 5 и ищется оставшейся частью алгоритма. ■
Также определим границу времени выполнения, используя (5.2).
(5.12) Время выполнения алгоритма равно O(n log n).
Доказательство. Исходная сортировка P по х и y выполняется за время O(n log n). Время выполнения оставшейся части алгоритма удовлетворяет рекуррентному отношению (5.1), а следовательно, равно O(n log n) согласно (5.2). ■