Задача о сумме подмножеств и задача о рюкзаке: добавление переменной - Динамическое программирование

Мы видим все больше примеров того, что область планирования предоставляет богатый источник алгоритмических задач, обладающих практическим смыслом. Ранее мы рассматривали задачи, в которых заявки задаются интервалом времени, а также задачи, в которых для заявки определяется продолжительность и предельное время, но не указывается конкретный интервал времени, в течение которого они должны выполняться.

В этом разделе рассматривается разновидность задач второго типа, с продолжительностями и предельным временем, которую трудно решать напрямую с использованием методов, применявшихся ранее. Для решения задачи будет применен метод динамического программирования, но с небольшими изменениями: “очевидного” множества подзадач оказывается недостаточно, и нам придется создавать расширенный набор подзадач. Как вы вскоре увидите, для этого в рекуррентное отношение, лежащее в основе динамической программы, будет добавлена новая переменная.

Задача

В рассматриваемой задаче планирования имеется одна машина, способная обрабатывать задания, и набор заявок {1, 2, ..., n}. Ресурсы могут обрабатываться только в период времени от 0 до W (для некоторого числа W). Каждая заявка представляет собой задание, для обработки которого требуется время w_i.

Если нашей целью является обработка заданий, при которой обеспечивается максимальная занятость машины до “граничного времени” W, какие задания следует выбрать?

В более формальном виде: имеются n элементов {1, ..., n}, каждому из которых присвоен неотрицательный вес w_i (для i = 1, ..., n). Также задана граница W. Требуется выбрать подмножество S элементов, для которого чтобы этого ограничения значение было как можно больше. Эта задача называется задачей о сумме подмножеств.

Она является естественным частным случаем более общей задачей, называемой задачей о рюкзаке, в которой у каждого элемента i имеется как значение v_i, так и вес w_i. Целью в этой общей задачи является нахождение подмножества с максимальным суммарным значением, при котором общий вес не превышает W. Название “задача о рюкзаке” происходит от аналогии с наполнением рюкзака емкостью W на максимальную часть объема (или максимальной стоимостью груза) с использованием подмножества элементов {1, ..., n}. При упоминании величин w_i и Wмы будем использовать термины “вес” и “время”.

Поскольку ситуация напоминает другие задачи планирования, уже встречавшиеся ранее, естественно спросить, можно ли найти оптимальное решение при помощи жадного алгоритма. Похоже, ответ на этот вопрос отрицателен — по крайней мере, не известно никакое эффективное жадное правило, которое всегда строит оптимальное решение. Один из естественных жадных методов основан на сортировки элементов по убыванию веса (или по крайней мере для всех элементов с весом, не превышающим W), а затем выборе элементов в этом порядке, пока общий вес остается меньше W. Но если значение Wкратно 2, и имеются три элемента с весами {W/2 + 1,W/2,W/2}, этот жадный алгоритм не обеспечит оптимального решения. Также можно провести сортировку по возрастанию веса, а затем проделать то же самое; но этот способ не работает для входных данных вида {1, W/2, W/2}.

В этом разделе мы постараемся показать, как применить динамическое программирование для решения задачи. Вспомните основные принципы динамического программирования: нужно перейти к небольшому количеству подзадач, чтобы каждая подзадача легко решалась по “меньшим” подзадачам, а решение исходной задачи легко строилось по известным решениям всех подзадач. Проблема в том, чтобы определить хорошее множество подзадач.

Разработка алгоритма

Неудачная попытка

В случае взвешенного интервального планирования сработала общая стратегия с рассмотрением подзадач, в которых задействованы только первые i заявок. Попробуем применить эту стратегию в данном случае. Лучшее возможное решение, использующее подмножество заявок {1, ..., i}, будет обозначаться OPT(i) (как это делалось ранее). В задаче взвешенного интервального планирования ключевой момент заключался в том, чтобы сосредоточиться на оптимальном решении O нашей задачи и рассмотреть два случая в зависимости от того, принимается или отвергается последняя заявка n этим оптимальным решением. Как и в том случае, одна из частей следует непосредственно из определения OPT(i).

♦ Если n ∉ O, то OPT(n) = OPT(n - 1).

Затем необходимо рассмотреть случай, в котором n ∈ O. Хотелось бы иметь простую рекурсию, которая сообщит лучшее возможное значение для решений, содержащих последнюю заявку n. Для взвешенного интервального планирования это было несложно, так как мы могли просто удалить каждую заявку, конфликтующую с n. В текущей задаче дело обстоит сложнее. Из принятия заявки n не следует, что какую-то другую заявку нужно отклонить, — а лишь то, что для подмножества принимаемых заявок S ⊆ {1, ..., n - 1} остается меньше свободного веса: вес w_nиспользуется для принятой заявки n, так что для множества S остальных принимаемых заявок остается только вес W - w_n (рис. 6.10).

Рис. 6.10. При включении в решение элемента n вес w_n занят и для остальных заявок остается доступный вес W - w_n

Улучшенное решение

Все это наводит на мысль, что решение потребует больше подзадач: для определения значения OPT(n) необходимо знать не только значение OPT(n - 1), но и лучшее решение, которое может быть получено с использованием подмножества первых n - 1 элементов и общего доступного веса W - w_n. А следовательно, подзадач будет намного больше: по одной для каждого исходного множества {1, ..., i} элементов и для каждого возможного значения оставшегося доступного веса w. Предположим, W — целое число, а все запросы i = 1, ..., n имеют целые веса w. Тогда подзадача создается для каждого i = 0,1, ..., n и каждого целого числа 0 ≤ w ≤ W. Для оптимального решения, использующего подмножество элементов {1, ..., i} с максимально допустимым весом w, будет использоваться решение OPT(i, w), то есть

где максимум определяется по подмножествам S ⊆ {1, ..., i}, удовлетворяющим условию С этим новым множеством подзадач мы сможем представить значение OPT(i, w) в виде простого выражения, использующего значения меньших подзадач. Более того, OPT(n, W) — значение, которое мы ищем в конечном итоге. Как и прежде, пусть O обозначает оптимальное решение исходной задачи.

♦ Если n ∉ O, то OPT(n, W) = OPT(n - 1, W), так как элемент n можно просто игнорировать.

♦ Если n ∈ O, то OPT(n, W) = w_n + OPT(n - 1, W- w_n), так как теперь ищется вариант оптимального использования оставшейся емкости W - w_n между элементами 1, 2, ..., n - 1.

Когда n-й элемент слишком велик, то есть W < w_n, должно выполняться условие OPT(n, W) = OPT(n - 1, W). В противном случае мы получаем оптимальное решение, допускающее все n заявок, выбирая лучший из этих двух вариантов. Применяя аналогичные рассуждения для подзадачи с элементами {1, ..., i} и максимальным допустимым весом w, получаем следующее рекуррентное отношение:

(6.8) Если w < w_i, то OPT(i, w) = OPT(i - 1, w). В противном случае OPT(i, w) = max(OPT(i - 1, w), w_i + OPT(i - 1, w – w_i)).

Как и прежде, мы хотим создать алгоритм, который строит таблицу всех значений OPT(i, w), вычисляя каждое из них не более одного раза.

При помощи (6.8) можно немедленно доказать посредством индукции, что возвращаемое значение M[n, W] является значением оптимального решения для заявок 1, ..., n и доступного веса W.

Анализ алгоритма

Вспомните одномерную последовательность ячеек для задачи взвешенного интервального планирования на рис. 6.5, где был представлен способ итеративного заполнения массива M для этого алгоритма. Для только что разработанного алгоритма можно использовать аналогичное представление, но на этот раз понадобится двумерная таблица, отражающая двумерный массив подзадач. На рис. 6.11 изображено построение подзадач в этой ситуации: значение M[i, w] вычисляется по двум другим значениямM[i - 1, w] и M[i - 1, w - w_i].

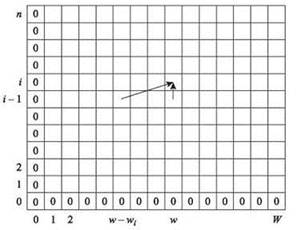
Рис. 6.11. Двумерная таблица значений OPT. Крайний левый столбец и нижняя строка всегда содержат 0. Значение OPT(i, w) вычисляется по двум другим элементам — OPT(i - 1, w) и OPT(i - 1, w - w_i) в соответствии со стрелками

В качестве примера выполнения этого алгоритма рассмотрим экземпляр с предельным весом W = 6 и n = 3 элементами с размерами w₁ = w₂ = 2 и w₃ = 3. Оптимальное значение OPT(3, 6) = 5 достигается при использовании третьего элемента и одного из первых двух элементов. На рис. 6.12 продемонстрирован процесс заполнения алгоритмом двумерной таблицы значениями OPTстрока за строкой.

Следующий вопрос — время выполнения алгоритма. Как и прежде в задаче взвешенного интервального планирования, мы строим таблицу решений M и вычисляем каждое из значений M[i, w] за время O(1) с использованием предыдущих значений. Следовательно, время выполнения пропорционально количеству элементов в таблице.

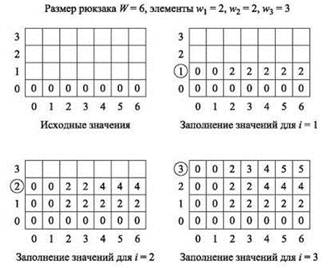
Рис. 6.12. Итерации алгоритма для простого экземпляра задачи о сумме подмножеств

(6.9) Алгоритм Subset-Sum(n, W) правильно вычисляет оптимальное значение для задачи и выполняется за время O(nW).

Обратите внимание: этот метод менее эффективен, чем динамическая программа для задачи взвешенного интервального планирования. В самом деле, его время выполнения не является полиномиальной функцией n; это полиномиальная функция n и W — наибольшего целого, задействованного в определении задачи. Такие алгоритмы называются псевдополиномиальными. Псевдополиномиальные алгоритмы могут обладать неплохой эффективностью при достаточно малых числах {w_i} во входных данных; с увеличением этих чисел их практическая применимость снижается.

Чтобы получить оптимальное множество элементов S, можно выполнить обратное отслеживание по массиву M по аналогии с тем, как это делалось в предыдущих разделах:

(6.10) Для таблицы M оптимальных значений подзадач оптимальное множество S может быть найдено за время O(n).

Расширение: задача о рюкзаке

Задача о рюкзаке немного сложнее задачи планирования, которая рассматривалась нами ранее. Возьмем ситуацию, в которой каждому элементу i поставлен в соответствие неотрицательный вес w_i, как и прежде, и отдельное значение v_i. Цель — найти подмножество S с максимальным значением в котором общий вес множества не превышает W:

Алгоритм динамического программирования несложно расширить до этой более общей задачи. Аналогичное множество подзадач OPT(i, w) используется для представления значения оптимального решения с использованием подмножества элементов {1, ..., i} и максимального доступного веса w. Рассмотрим оптимальное решение O и определим два случая в зависимости от того, выполняется ли условие n ∈ O:

♦ Если n ∉ O, то OPT(n, W) = OPT(n - 1, W).

♦ Если n ∈ O, то OPT(n, W) = v_n + OPT(n - 1, W - w_n).

Применение этой аргументации к подзадачам приводит к следующей аналогии с (6.8).

(6.11) Если w < w_i, то OPT(i, w) = OPT(n - 1, w). В противном случае OPT(i, w) = max(OPT(i - 1, w), v_i + OPT(i - 1, w - w_i)).

При помощи этого рекуррентного отношения можно записать полностью аналогичный алгоритм динамического программирования, из чего вытекает следующий факт:

(6.12) Задача о рюкзаке решается за время O(nW).