Алгоритмы - Разработка и применение - 2016 год
Выравнивание последовательностей - Динамическое программирование
В оставшейся части главы рассматриваются еще два алгоритма динамического программирования, находящие широкое практическое применение. В следующих двух разделах рассматривается выравнивание последовательностей — фундаментальная задача, встречающаяся при сравнении строк. Затем мы обратимся к задаче вычисления кратчайших путей в графах, которые могут содержать ребра с отрицательной стоимостью.
Задача
Словари в Интернете становятся все более удобными: часто бывает проще открыть сетевой словарь по закладке, чем снимать бумажный словарь с полки. К тому же многие электронные словари предоставляют возможности, отсутствующие в бумажных словарях: если вы ищете определение и введете слово, отсутствующее в словаре (например, ocurrance), словарь поинтересуется: “Возможно, вы имели в виду occurrence?” Как он это делает? Он действительно знает, что происходит у вас в голове?
Отложим второй вопрос до другой книги, а пока поразмыслим над первым. Чтобы решить, что вы могли иметь в виду, наиболее естественно провести в словаре поиск слова, наиболее “похожего” на введенное. Для этого нужно ответить на вопрос: как определить сходство между двумя словами или строками?
Интуитивно понятно, что “ocurrance” и “occurrence” похожи, потому что для совпадения этих двух слов достаточно добавить c в первое слово и заменить a на e. Так как ни одно из этих изменений не кажется слишком значительным, можно сделать вывод о том, что между этими двумя словами существует серьезное сходство. Иначе говоря, эти два слова можно выстроить параллельно, буква за буквой:
![]()
Дефис (-) обозначает разрыв, который нужно добавить в первое слово для совмещения его со вторым. Более того, расположение не идеально, поскольку буква e стоит напротив a.
Нужно построить модель, в которой сходство оценивается по количеству разрывов и несовпадений, возникающих при параллельном размещении двух слов. Конечно, слова можно разместить многими разными способами, например:
![]()
с тремя разрывами и без несовпадений. Что лучше: один разрыв и одно несовпадение или три разрыва без несовпадений?
Обсуждение упрощалось тем, что мы приблизительно представляли, как должно выглядеть соответствие. Если две строки не похожи на английскую слова (например, abbbaabbbbaab и ababaaabbbbbab), решить, можно их выстроить параллельно или нет, становится сложнее:
![]()
Электронные словари и системы проверки орфографии — не самые требовательные приложения такого типа. Оказывается, определение сходства между строками является одной из основных вычислительных задач, которые приходится решать в наши дни специалистам по молекулярной биологии.
Строки встречаются в биологии абсолютно естественно: геном организма (полный набор его генетического материала) делится на гигантские линейные молекулы ДНК, называемые хромосомами, каждая из которых может рассматриваться как одномерное химическое устройство хранения информации. Более того, можно вполне адекватно представить себе хромосому как огромную ленту, на которой записана строка из символов алфавита {A, C, G, T}. В этой строке закодированы инструкции по построению белковых молекул; используя химический механизм для чтения частей хромосомы, клетка может строить белки, которые, в свою очередь, управляют ее метаболизмом.
Почему сходству отводится важная роль в этой картине? В первом приближении последовательность символов в геноме организма может рассматриваться как определение свойств организма. Предположим, имеются два штамма бактерий X и Y, между которыми существует тесная эволюционная связь. Также допустим, что нам удалось определить, что некоторая подстрока в ДНК X кодирует некоторую разновидность токсина. Если удастся обнаружить очень “похожую” подстроку в ДНК Y, еще до проведения каких-либо экспериментов можно будет выдвинуть гипотезу, что эта часть ДНК Y кодирует аналогичный токсин. Подобное применение вычислений для принятия решений о биологических экспериментах стало одной из характерных особенностей современной вычислительной биологии.
Итак, мы приходим к вопросу, который был задан изначально применительно к вводу неправильных слов в электронный словарь: как определить концепцию сходства между двумя строками?
В начале 1970-х годов молекулярные биологи Нидлман и Вунш предложили определение сходства, которое практически в неизменном виде стало стандартным определением, используемым в наши дни. Его положение как стандарта подкреплялось простотой и интуитивной привлекательностью, а также тем фактом, что оно было независимо открыто несколькими учеными примерно в одно время. Кроме того, к определению сходства прилагался эффективный алгоритм динамического программирования для его вычисления. Таким образом, парадигма динамического программирования была независимо открыта биологами примерно через 20 лет после того, как она была впервые сформулирована математиками и специалистами по информатике.
В основу определения заложены соображения, изложенные выше, и особенно концепция “выстраивания в линию” двух строк. Допустим, имеются две строки X и Y; строка X содержит последовательность символов x1, x2, ..., xm, а строка Y — последовательность символов y1, y2, ..., yn. Рассмотрим множества {1, 2, ..., m} и {1, 2, ..., n}, представляющие разные позиции в строках X и Y, и рассмотрим паросочетание этих множеств (напомним, что паросочетанием называется множество упорядоченных пар, обладающее тем свойством, что каждый элемент входит не более чем в одну пару). Паросочетание M этих двух множеств называется выравниванием при отсутствии “пересекающихся” пар: если (i, j), (i', j') ∈ M и i < i', то j < j'. На интуитивном уровне выравнивание предоставляет способ параллельного расположения двух строк: оно сообщает, какие пары позиций будут находиться друг напротив друга. Например,
![]()
соответствует выравниванию {(2, 1), (3, 2), (4, 3)}.
Наше определение сходства будет основано на нахождении оптимального выравнивания между X и Y по следующему критерию. Предположим, M — заданное выравнивание между X и Y.
♦ Во-первых, должен существовать параметр δ > 0, определяющий штраф за разрыв. Для каждой позиции X или Y, не имеющей пары в M (то есть разрыва), вводится штраф δ.
♦ Во-вторых, для каждой пары букв p, q в нашем алфавите существует штраф за несоответствиеαpq за совмещение p с q. Таким образом, для всех (i, j) ∈ M совмещение хi с yj приводит к выплате соответствующего штрафа за несоответствие ![]() В общем случае предполагается, что αрр = 0 для любого символа р, то есть совмещение символа со своей копией не приводит к штрафу за несоответствие — хотя это предположение не является обязательным для каких-либо дальнейших рассуждений.
В общем случае предполагается, что αрр = 0 для любого символа р, то есть совмещение символа со своей копией не приводит к штрафу за несоответствие — хотя это предположение не является обязательным для каких-либо дальнейших рассуждений.
♦ Стоимость выравнивания M вычисляется как сумма штрафов за разрывы и несоответствия. Требуется найти выравнивание с минимальной стоимостью.
В литературе по биологии процесс минимизации стоимости часто называется выравниванием последовательностей. Величины δ и {αpq} представляют собой внешние параметры, которые должны передаваться программе для выравнивания последовательностей; и действительно, значительная часть работы связана с выбором значений этих параметров. При разработке алгоритма выравнивания последовательностей мы будем рассматривать их как заданные извне. Возвращаясь к первому примеру, обратите внимание на то, как эти параметры определяют, какое из выравниваний ocurrance и occurrence следует предпочесть: первый вариант строго лучше других в том и только в том случае, если δ + αae < 3δ.
Разработка алгоритма
Для оценки сходства между строками X и Y имеется конкретное числовое определение: это минимальная стоимость выравнивания между X и Y. Чем ниже эта стоимость, тем более похожими объявляются строки. Теперь обратимся к задаче вычисления этой минимальной стоимости и оптимального выравнивания, которое обеспечивает эту стоимость для заданной пары строк X и Y.
Для решения этой задачи можно попытаться применить динамическое программирование, руководствуясь следующей базовой дихотомией.
♦ В оптимальном выравнивании M либо (m, n) ∈ M, либо (m, n) ∉ M. (То есть два последних символа двух строк либо сопоставляются друг с другом, либо нет.)
Самого по себе этого факта недостаточно для того, чтобы предоставить решение методом динамического программирования. Однако предположим, что он дополняется следующим базовым фактом:
(6.14) Пусть M — произвольное выравнивание X и Y. Если (m, n) ∉ M, то либо m-я позиция X, либо n-я позиция Y не имеют сочетания в M.
Доказательство. Действуя от обратного, предположим, что (m, n) ∉ M и существуют числа i < m и j < n, для которых (m, j) ∈ M и (i, n) ∈ M. Но это противоречит нашему определению выравнивания: имеем (i, n), (m, j) ∈ M с i < m, но n > i, поэтому пары (i, n) и (m, j) пересекаются. ■
Существует эквивалентный вариант записи (6.14) с тремя альтернативными возможностями, приводящий напрямую к формулировке рекуррентного отношения.
(6.15) В оптимальном выравнивании M истинно хотя бы одно из следующих трех условий:
♦ (i) (m, n) ∈ M; или
♦ (ii) m-я позиция X не имеет сочетания; или
♦ (iii) n-я позиция Y не имеет сочетания.
Теперь пусть 0РТ(i, j) обозначает минимальную стоимость выравнивания между х1x2 ... хi и y1y2 ... yj. Если выполняется условие (i) из (6.15), мы платим ![]() и выравниваем x1x2 ... xm-1 с y1y2... yn-1 настолько хорошо, насколько это возможно; получаем
и выравниваем x1x2 ... xm-1 с y1y2... yn-1 настолько хорошо, насколько это возможно; получаем ![]() Если выполняется условие (ii), мы платим штраф за разрыв δ, потому что m-я позиция X не имеет сочетания, и выравниваем x1x2 ... xm-1 с y1y2 ... yn-1 настолько хорошо, насколько это возможно. В этом случае получаем OPT(m, n) = δ + OPT(m - 1, n). Аналогичным образом для случая (iii) получаем OPT(m, n) = δ + OPT(m, n - 1).
Если выполняется условие (ii), мы платим штраф за разрыв δ, потому что m-я позиция X не имеет сочетания, и выравниваем x1x2 ... xm-1 с y1y2 ... yn-1 настолько хорошо, насколько это возможно. В этом случае получаем OPT(m, n) = δ + OPT(m - 1, n). Аналогичным образом для случая (iii) получаем OPT(m, n) = δ + OPT(m, n - 1).
Используя аналогичные рассуждения для подзадачи нахождения выравнивания с минимальной стоимостью для х1x2 ... хi и y1y2 ... yj, приходим к следующему факту:
(6.16) Стоимости минимального выравнивания удовлетворяют следующему рекуррентному отношению для i ≥ 1 и j ≥ 1:
![]()
Кроме того, (i, j) принадлежит оптимальному выравниванию M для этой подзадачи в том и только в том случае, если минимум достигается на первом из этих значений.
Мы добрались до точки, в которой алгоритм динамического программирования стал ясен: мы строим значения OPT(i, j), используя рекуррентное отношение в (6.16). Существуют только O(mn) подзадач, и OPT(m, n) дает искомое значение.
Теперь определим алгоритм для вычисления значения оптимального выравнивания. Для выполнения инициализации заметим, что OPT(i, 0) = OPT(0, i) = iδ для всех i, так как совместить i-буквенное слово с 0-буквенным словом возможно только с использованием i разрывов.

Как и в случае с предыдущими алгоритмами динамического программирования, построение самого выравнивания осуществляется обратным отслеживанием по массиву A с использованием второй части факта (6.16).
Анализ алгоритма
Правильность алгоритма следует непосредственно из (6.16). Время выполнения равно O(mn), так как массив A содержит только O(mn) элементов и в худшем случае на каждый тратится постоянное время.
У алгоритма выравнивания последовательностей существует элегантное визуальное представление. Допустим, имеется двумерный решетчатый граф GXY с размерами m х n; строки помечены символами X, столбцы помечены символами Y, а ребра направлены так, как показано на рис. 6.17.
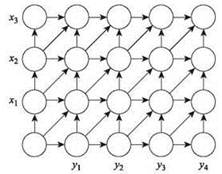
Рис. 6.17. Представление выравнивания последовательностей в форме графа
Строки нумеруются от 0 до m, а столбцы от 0 до n; узел на пересечении i-й строки иj-го столбца обозначается (i, j). Ребрам GXY назначаются стоимости: стоимость каждого горизонтального и вертикального ребра равна δ, а стоимость диагонального ребра из (i - 1, j - 1) в (i, j) равна ![]()
Теперь смысл этой схемы становится понятным: рекуррентное отношение для OPT(i, j) из (6.16) в точности соответствует рекуррентному отношению для пути минимальной стоимости от (0, 0) до (i, j) в GXY. Следовательно, мы можем показать
(6.17) Пусть f (i, j) — стоимость минимального пути из (0, 0) в (i, j) в GXY. Тогда для всех i, j выполняется условие f (i, j) = OPT(i, j).
Доказательство. Утверждение легко доказывается индукцией по i + j. Если i + j = 0, значит, i = j = 0, и тогда f(i, j) = OPT(i, j) = 0.
Теперь рассмотрим произвольные значения i и j и предположим, что утверждение истинно для всех пар (i', j') с i' + j' < i + j. Последнее ребро кратчайшего пути к (i, j) проходит либо из (i - 1, j - 1), либо из (i - 1, j), либо из (i, j - 1). Следовательно, имеем
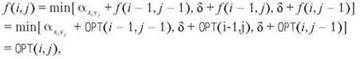
Переход от первой строки ко второй осуществляется по индукционной гипотезе, а переход от второй к третьей — по (6.16). ■
Таким образом, значение оптимального выравнивания равно длине кратчайшего пути в GXY от (0,0) до (m, n). (Любой путь в Gху из (0,0) в (m, n) будет называться путем из угла в угол.) Более того, диагональные ребра, используемые в кратчайшем пути, точно соответствуют парам выравнивания с минимальной стоимостью. Эти связи в задаче нахождения кратчайшего пути в графе Gху не приводят к прямому улучшению времени выполнения для задачи выравнивания последовательностей; однако они способствуют интуитивному пониманию задачи, а также помогают в поиске алгоритмов для более сложных видов выравнивания последовательностей.
Например, на рис. 6.18 приведены значения кратчайшего пути из (0, 0) в каждый из узлов (i, j) для задачи выравнивания слов mean и name. В контексте нашего примера предполагается, что δ = 2; стоимость сочетания гласной с другой гласной или согласной с другой согласной равна 1; стоимость сочетания гласной с согласной равна 3. Для каждой ячейки в таблице (представляющей соответствующий узел) стрелкой обозначается последний шаг кратчайшего пути, ведущего к этому узлу, — другими словами, вариант достижения минимума в (6.16). Следовательно, возвращаясь по стрелкам в обратном направлении от узла (4, 4), можно построить выравнивание методом обратного отслеживания.
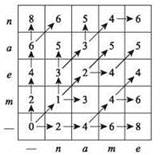
Рис. 6.18. Значения OPT для задачи выравнивания слов mean и name