Алгоритмы - Разработка и применение - 2016 год
Полиномиальное сведение - NP-полнота и вычислительная неразрешимость
Мы подошли к одной из важнейших переходных точек в книге. До сих пор мы разрабатывали эффективные алгоритмы для самых разнообразных задач и даже добились некоторых результатов в неформальной классификации задач, имеющих эффективные решения, — например, задач, которые могут быть выражены минимальными разрезами графа, или задачам, которые формулируются средствами динамического программирования. Но хотя при этом мы нередко отмечали другие задачи, для которых не могли предложить решения, никакие попытки реальной классификации или описания категорий задач, не имеющих эффективного решения, не предпринимались.
В самом начале книги, когда приводились первые основополагающие определения, мы договорились о том, что нашим рабочим критерием эффективности будет полиномиальное время выполнения. Как упоминалось ранее, у такого конкретного определения есть одно важное преимущество: оно позволяет привести математическое доказательство того, что некоторые задачи не могут быть решены при помощи алгоритмов с полиномиальным временем (то есть “эффективных”).
Когда ученые занялись серьезными исследованиями вычислительной сложности, им удалось сделать первые шаги к доказательству того, что эффективных алгоритмов для решения некоторых особенно сложных задач не существует. Но для многих фундаментальных дискретных вычислительных задач (из области оптимизации, искусственного интеллекта, комбинаторики, логики и т. д.) этот вопрос оказался слишком сложным и с тех пор так и остается открытым: алгоритмы с полиномиальным временем для таких задач неизвестны, но и доказательств того, что таких алгоритмов не существует, пока нет.
В свете этой формальной неоднозначности, которая только укреплялась с течением времени, в области изучения вычислительной сложности был достигнут заметный прогресс. Ученым удалось охарактеризовать широкий спектр задач в этой “серой зоне” и доказать их эквивалентность в следующем смысле: если для одной из таких задач будет найден алгоритм с полиномиальным временем выполнения, это будет означать существование алгоритма для всех таких задач. Такие задачи называются NP-полными, — смысл этого термина вскоре станет более понятен. Существуют буквально тысячи NP-полных задач в самых разных областях; похоже, этот класс содержит значительную долю фундаментальных задач, сложность которых не поддается разрешению. Формулировка NP-полноты и доказательство эквивалентности всех таких задач в действительности являются весьма значительным результатом: это означает, что все эти открытые вопросы в действительности представляют собой один открытый вопрос, один тип сложности, который мы пока не понимаем в полной мере.
С практической точки зрения NP-полнота фактически означает “запредельную вычислительную сложность, хотя мы пока не можем этого доказать”. Доказательство того, что задача является NP-полной, становится веской причиной для прекращения поисков эффективного алгоритма. С таким же успехом можно искать эффективный алгоритм для любой другой знаменитой вычислительной задачи, которая заведомо является NP-полной; многие ученые пытались найти эффективные алгоритмы для таких задач — но пока безуспешно.
8.1. Полиномиальное сведение
Мы намереваемся исследовать пространство вычислительно сложных задач, чтобы в конечном итоге прибыть к математической характеристике большого класса. Основным приемом в этом исследовании будет сравнение относительной сложности разных задач; нам хотелось бы найти формальное выражение для таких утверждений, как “задача X обладает как минимум не меньшей сложностью, чем задача Y”. Для формализации будет применен метод сведения: чтобы показать, что некоторая задача X по меньшей мере не менее сложна, чем другая задача Y, мы докажем, что “черный ящик”, способный решить задачу X, также сможет решить задачу Y. (Другими словами, решение X будет достаточно мощным для того, чтобы также решить Y.)
Чтобы точно выразить этот критерий, мы предположим, что задача X в нашей вычислительной модели может быть напрямую решена с полиномиальным временем. Допустим, имеется некий “черный ящик”, способный решать экземпляры задачи X; если передать ему входные данные для экземпляра X, то “черный ящик” за один шаг вернет правильный ответ. А теперь зададимся следующим вопросом:
(*) Возможно ли решить произвольный экземпляр задачи Y с полиномиальным количеством стандартных вычислительных шагов, дополняемых полиномиальным количеством обращений к “черному ящику”, решающему задачу X?
Если ответ на этот вопрос положителен, то мы используем запись Y≤PX; это читается как “задача Y является полиномиальносводимой к X”, или “сложность X по крайней мере не меньше сложности Y (в отношении полиномиального времени)”. Обратите внимание: в этом определении учитываются затраты времени на передачу входных данных “черному ящику”, решающему X, и на получение ответа от “черного ящика”.
Такая формулировка сводимости чрезвычайно естественна. Когда мы задаемся вопросом о сводимости к задаче X, все выглядит так, словно вычислительная модель дополняется специализированным процессором, решающим экземпляры X за один шаг. А теперь разберемся, какую же вычислительную мощь предоставляет нам этот специализированный процессор?
У нашего определения ≤р имеется одно важное следствие: предположим, Y≤PX и существует алгоритм с полиномиальным временем для решения X. Тогда польза от специализированного “черного ящика” для X не столь уж велика; его можно заменить алгоритмом с полиномиальным временем для X. Подумайте, что произойдет с нашим алгоритмом для задачи Y, использующим полиномиальное количество шагов плюс полиномиальное количество вызовов “черного ящика”. Он превращается в алгоритм, использующий полиномиальное количество шагов плюс полиномиальное количество вызовов процедуры, выполняемой за полиномиальное время; другими словами, он превращается в алгоритм с полиномиальным временем. Таким образом, мы доказали следующий факт.
(8.1) Допустим, Y≤PX. Если задача X решается за полиномиальное время, то и задача Y может быть решена за полиномиальное время.
Собственно, этот факт, хотя и неявно, уже использовался ранее в книге. Вспомните, как мы решали задачу о двудольном паросочетании с использованием полиномиального объема предварительной обработки и времени решения одного экземпляра задачи о максимальном потоке. Так как задача о максимальном потоке может быть решена за полиномиальное время, мы заключили, что это возможно и для задачи о двудольном паросочетании. Кроме того, задача сегментации изображения решалась с использованием полиномиального объема предварительной обработки и времени решения одного экземпляра задачи о минимальном разрезе с теми же последствиями. Оба примера могут рассматриваться как прямые применения (8.1). В самом деле, (8.1) предоставляет отличный способ разработки алгоритмов с полиномиальным временем для новых задач: сведение к задаче, которую мы уже умеем решать за полиномиальное время.
Тем не менее в этой главе (8.1) будет использоваться для установления вычислительной неразрешимости некоторых задач. Мы будем заниматься довольно нетривиальным делом: речь пойдет об оценке разрешимости задач даже в том случае, когда мы не знаем, как решать их за полиномиальное время. Для этой цели будет использовано утверждение, противоположное (8.1); оно достаточно важно, чтобы представить его как отдельный факт.
(8.2) Допустим, Y≤рX. Если задача Yне решается за полиномиальное время, то и задача X не может быть решена за полиномиальное время.
Утверждение (8.2) очевидно эквивалентно (8.1), но оно подчеркивает наш общий план: если имеется заведомо сложная задача Y и мы показываем, что Y≤рX, то сложность “распространяется” на X; задача X должна быть сложной, или в противном случае она могла бы использоваться для решения Y.
Так как на практике мы не знаем, возможно ли решить изучаемые задачи за полиномиальное время или нет, обозначение ≤р будет использоваться для установления относительной сложности между задачами.
С учетом сказанного можно установить некоторые отношения сводимости между исходным набором фундаментально сложных задач.
Первое сведение: независимое множество и вершинное покрытие
Задача о независимом множестве, представленная в числе пяти типичных задач в главе 1, послужит первым прототипным примером сложной задачи. Алгоритм с полиномиальным временем для нее неизвестен, но мы также не знаем, как доказать, что такого алгоритма не существует.
Вернемся к формулировке задачи о независимом множестве, так как в нее будет добавлен один нюанс. Вспомните, что в графе G = (V, E) множество узлов S ⊆ V называется независимым, если никакие два узла в S не соединены ребром. Найти малое независимое множество в графе несложно (например, одиночный узел образует независимое множество); трудности возникают при поиске больших независимых множество так как требуется построить большой набор узлов, в котором нет соседних узлов. Например, множество узлов {3, 4, 5} является независимым множеством размера 3 в графе на рис. 8.1, тогда как множество узлов {1, 4, 5, 6} является независимым множеством большего размера.
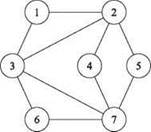
Рис. 8.1. Граф, для которого размер наибольшего независимого множества равен 4, а наименьшее вершинное покрытие имеет размер 3
В главе 1 была представлена задача нахождения наибольшего независимого множества в графе G. В контексте нашего текущего исследования, направленного на сводимость задач, намного удобнее работать с задачами, на которые можно ответить только “да/нет”, поэтому задача о независимом множестве будет сформулирована следующим образом:
Для заданного графа G и числа к содержит ли G независимое множество с размером не менее к?
С точки зрения разрешимости с полиномиальным временем оптимизационная версия задачи (найти максимальный размер независимого множества) не так уж сильно отличается от версии с проверкой условия (решить, существует ли в G независимое множество с размером не менее заданного k, — да или нет). Зная метод решения первой версии, мы автоматически решим вторую (для произвольного k). Но также существует чуть менее очевидный обратный факт: если мы можем решить версию задачи о независимом множестве с проверкой условия для всех k, то мы также можем найти максимальное независимое множество. Для заданного графа G с n узлами версия с проверкой условия просто проверяется для каждого k; наибольшее значение к, для которого ответ будет положительным, является размером наибольшего независимого множества в G. (А при использовании бинарного поиска достаточно применить версию с проверкой условия для O(log n) разных значений k.) Простая эквивалентность между проверкой условия и оптимизацией также встречается в задачах, которые будут рассматриваться ниже.
Теперь для демонстрации нашей стратегии по установлению связи между сложными задачами будет рассмотрена другая фундаментальная задача из теории графов, для которой неизвестен эффективный алгоритм: задача о вершинном покрытии. Для заданного графа G = (V, E) множество узлов S ⊆ V образует вершинное покрытие, если у каждого ребра е ∈ E по крайней мере один конец принадлежит S.
Обратите внимание на один нюанс: в задаче о вершинном покрытии в данном случае вершины “покрывают”, а ребра являются “покрываемыми объектами”. Найти большое вершинное покрытие для графа несложно (например, полное множество вершин); трудно найти покрытие меньшего размера. Задача о вершинном покрытии формулируется следующим образом.
Для заданного графа G и числа k содержит ли G вершинное покрытие с размером не более k?
Например, для графа на рис. 8.1 множество узлов {1, 2, 6, 7} является вершинным покрытием с размером 4, а множество {2, 3, 7} является вершинным покрытием с размером 3.
Мы не знаем, как решить задачу о независимом множестве или задачу о вершинном покрытии за полиномиальное время; но что можно сказать об их относительной сложности? Сейчас мы покажем, что эти задачи имеют эквивалентную сложность; для этого мы установим, что Независимое множество ≤р Вершинное покрытие, а также Вершинное покрытие ≤р Независимое множество. Это напрямую вытекает из следующего факта.
(8.3) Имеется граф G = (V, E). S является независимым множеством в том и только в том случае, если его дополнение V-S является вершинным покрытием.
Доказательство. Предположим, что S является независимым множеством. Рассмотрим произвольное ребро e = (u, v). Из независимости S следует, что u и v не могут одновременно принадлежать S; следовательно, один из этих концов должен принадлежать V-S. Отсюда следует, что у каждого ребра как минимум один конец принадлежит V-S, а значит, V-S является вершинным покрытием.
И наоборот, предположим, что V-S является вершинным покрытием. Рассмотрим два любых узла u и v в S. Если бы они были соединены ребром е, то ни один из концов e не принадлежал бы V-S, что противоречило бы предположению о том, что V-S является вершинным покрытием. Отсюда следует, что никакие два узла в S не соединены ребром, а значит, S является независимым множеством. ■
Сведения в обе стороны между двумя задачами следуют напрямую из (8.3).
(8.4) Независимое множество ≤р Вершинное покрытие.
Доказательство. Имея “черный ящик” для решения задачи о вершинном покрытии, мы могли бы решить, содержит ли G независимое множество с размером не менее k, обратившись к “черному ящику” с вопросом о том, содержит ли G вершинное покрытие с размером не более n - k. ■
(8.5) Вершинное покрытие ≤р Независимое множество.
Доказательство. Имея “черный ящик” для решения задачи о независимом множестве, мы могли бы решить, содержит ли G вершинное покрытие в размером не более k, обратившись к “черному ящику” с вопросом о том, содержит ли G независимое множество с размером не менее n - k. ■
Итак, приведенный анализ поясняет наш план в целом: хотя мы не знаем, как эффективно решать задачу о независимом множестве или задачу о вершинном покрытии, из (8.4) и (8.5) следует, что решение любой задачи предоставит эффективное решение другой, то есть эти два факта устанавливают относительные уровни сложности этих задач.
Применим эту стратегию для ряда других задач.
Сведение к более общему случаю: вершинное покрытие к покрытию множества
Задача о независимом множестве и задача о вершинном покрытии представляют собой две разные категории задач. Задача о независимом множестве может рассматриваться как “задача упаковки”: требуется “упаковать” как можно больше вершин с учетом конфликтов (ребер), препятствующих нам в этом. С другой стороны, задача о вершинном покрытии может рассматриваться как “задача покрытия”: требуется экономно “накрыть” все ребра в графе с использованием минимального количества вершин.
Задача о вершинном покрытии представляет собой задачу покрытия, сформулированную “на языке” графов; существует более общая задача покрытия — задача покрытия множества, в которой требуется покрыть произвольное множество объектов с использованием нескольких меньших множеств. Мы можем сформулировать задачу покрытия множества следующим образом:
Задано множеств U из n элементов, набор S1, ..., Sm подмножеств U и число k.
Существует ли набор из не более чем к таких множеств, объединение которых равно всему множеству U?
Представьте, например, что имеются m программных компонентов и множество U из n функций, которыми должна обладать система. i-й компонент реализует множество Si ⊆ U функций. В задаче покрытия множества требуется включить небольшое количество компонентов, чтобы система поддерживала все n функций.
На рис. 8.2 изображен пример задачи покрытия множества: десять кругов представляют элементы основного множества U, а семь овалов и многоугольников — множества S1, S2, ..., S7. В этом экземпляре задачи присутствует совокупность множеств, объединение которых равно U: например, можно выбрать высокий овал слева с двумя многоугольниками.
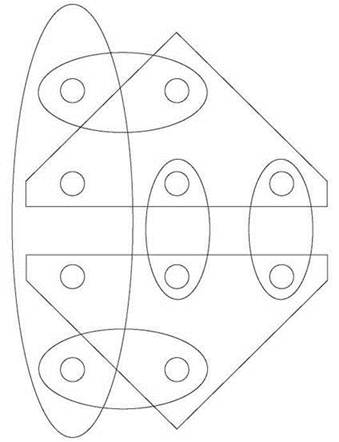
Рис. 8.2. Пример задачи покрытия множества
На интуитивном уровне понятно, что задача вершинного покрытия является особым случаем задачи покрытия множества: в последнем случае мы пытаемся покрыть произвольное множество произвольными подмножествами, тогда как в первом ставится частная задача покрытия ребер графа с использованием множеств ребер, инцидентных вершинам. Более того, можно доказать следующее сведение.
(8.6) Вершинное покрытие ≤р Покрытие множества.
Доказательство. Допустим, имеется “черный ящик”, который умеет решать задачу о покрытии множества, и произвольный экземпляр задачи о вершинном покрытии, заданный графом G = (V, E) и числом k. Как использовать “черный ящик” для решения этой задачи?
Наша цель — найти покрытие для ребер E, поэтому мы формулируем экземпляр задачи покрытия множества, в которой универсальное множество U равно E. Каждый раз, когда мы выбираем вершину в задаче вершинного покрытия, мы покрываем все ребра, инцидентные этой вершине; следовательно, для каждой вершины i ∈ V в экземпляр задачи покрытия множества добавляется множество Si ⊆ U, состоящее из всех ребер G, инцидентных i.
Утверждается, что U может быть покрыто с использованием не более k из множеств S1, ..., Sn в том, и только в том случае, если G имеет вершинное покрытие с размером не более k. Это утверждение доказывается очень просто. Если l ≤ k множеств Si1, ..., Sil покрывают U, то каждое ребро в G инцидентно одной из вершин i1, ..., il, а значит, множество {i1, ..., il} является вершинным покрытием G с размером l ≤ k. И наоборот, если {i1, ..., il} является вершинным покрытием G с размером l ≤ k, то множества Si1, ..., Sil, покрывают U.
Итак, для заданного экземпляра задачи о вершинном покрытии формулируется экземпляр задачи покрытия множества, описанный выше, который передается “черному ящику”. Положительный ответ на исходный вопрос дается в том, и только в том случае, если “черный ящик” отвечает положительно.
(Вы можете убедиться в том, что экземпляр задачи покрытия множества на рис. 8.2 действительно соответствует полученному в ходе сведения, — начните с графа на рис. 8.1). ■
Обратите внимание на один важный момент, относящийся как к доказательству, так и к предшествующим сведениям в (8.4) и (8.5). Хотя определение ≤р позволяет выдать много обращений к “черному ящику” для задачи покрытия множества, мы выдали только одно. В самом деле, наш алгоритм вершинного покрытия состоял просто из кодирования задачи в один экземпляр задачи покрытия множества и последующего использования полученного ответа как ответа на общую задачу. Это относится практически ко всем сведениям, которые мы будем рассматривать; в них отношение Y≤рX будет устанавливаться преобразованием экземпляра Y в один экземпляр X, передачей “черному ящику” этого экземпляра X и использованием полученного ответа для экземпляра Y.
Подобно тому как задача покрытия множества является естественным обобщением задачи о вершинном покрытии, существует естественное обобщение задачи о независимом множестве как задачи упаковки для произвольных множеств. А именно задача упаковки множества определяется следующим образом:
Для заданного множества U из n элементов, набора S1, ..., Sm подмножеств U и числа k существует ли набор из минимум к таких подмножеств, из которых никакие два не пересекаются?
Иначе говоря, мы хотим “упаковать” большое количество множеств с тем ограничением, что никакие два из них не пересекаются.
Рассмотрим пример ситуации, в которой может возникнуть такая задача. Допустим, имеется множество U ресурсов, используемых в монопольном режиме, и множество из m программных процессов. Для выполнения i-го процесса необходимо множество ресурсов Si ⊆ U. Таким образом, задача упаковки множества ищет большую совокупность процессов, которые могут выполняться одновременно, без перекрытия требований к ресурсам (то есть без конфликтов).
Это естественная аналогия (8.6), а ее доказательство почти не отличается от приведенного; подробности остаются читателю для самостоятельной работы.
(8.7) Независимое множество ≤р Упаковка множества.