Алгоритмы - Разработка и применение - 2016 год
Задачи упорядочения - NP-полнота и вычислительная неразрешимость
До настоящего момента рассматривались задачи, которые (как, например, задачи о независимом множестве и вершинном покрытии) подразумевали перебор подмножеств набора объектов; также были представлены задачи (как, например, 3-SAT), основанные на поиске комбинаций 0/1 в наборе переменных. Еще один тип вычислительно сложных задач связан с поиском по множеству всех перестановок коллекции объектов.
Задача коммивояжера
Вероятно, самой известной из задач упорядочения является задача коммивояжера. Представьте коммивояжера, который должен посетить n городов v1, v2, ..., vn. Коммивояжер начинает с города v1, в котором он живет, и хочет найти маршрут — порядок, в котором он посетит все остальные города и вернется домой. Требуется найти маршрут с минимальным суммарным расстоянием всех поездок.
Чтобы формализовать эту задачу, мы воспользуемся предельно обобщенной концепцией расстояния: для каждой упорядоченной пары городов (vi, vj) задается неотрицательное число d(vi, vj), которое считается расстоянием от vi до vj. От расстояний не требуется ни симметричность (может оказаться, что d(vi, vj) ≠ d(vj, vi)), ни выполнение неравенства треугольника (сумма d(vi, vj) и d(vj, vk) может быть меньше “прямого” расстояния d(v.,vk)). Это делается для того, чтобы формулировка задачи была как можно более общей. Дело в том, что задача коммивояжера естественным образом встречается во многих приложениях, которые не имеют отношения к городам и коммивояжерам. Например, формулировка задачи коммивояжера применяется в таких областях, как планирование оптимальных перемещений манипулятора, который должен просверлить отверстия в n точках на поверхности микросхемы; или для обслуживания запросов ввода/вывода к диску; или для упорядочения выполнения n программных модулей для минимизации времени переключения контекста.
Итак, для заданного множества расстояний требуется упорядочить города в маршрут ![]() с i1 = 1, чтобы свести к минимуму общее расстояние
с i1 = 1, чтобы свести к минимуму общее расстояние ![]() Требование i1 = 1 просто “ориентирует” маршрут так, чтобы он начинался в исходном городе, а слагаемые в сумме просто задают расстояние от текущего города в маршруте до следующего. (Последнее слагаемое в сумме определяет расстояние, необходимое для того, чтобы коммивояжер мог вернуться домой в конце маршрута.)
Требование i1 = 1 просто “ориентирует” маршрут так, чтобы он начинался в исходном городе, а слагаемые в сумме просто задают расстояние от текущего города в маршруте до следующего. (Последнее слагаемое в сумме определяет расстояние, необходимое для того, чтобы коммивояжер мог вернуться домой в конце маршрута.)
А вот как выглядит задача коммивояжера в версии с принятием решения:
Для заданного набора расстояний между n городами и границы D существует ли маршрут, длина которого не превышает D?
Задача о гамильтоновом цикле
У задачи коммивояжера имеется естественная аналогия, которая образует одну из фундаментальных задач в теории графов. Для заданного направленного графа G = (V, E) цикл C в графе Gназывается гамильтоновым циклом, если он посещает каждую вершину ровно один раз, — иначе говоря, он “обходит” все вершины без повторений. Например, направленный граф на рис. 8.6 содержит несколько гамильтоновых циклов; в одном из них узлы посещаются в порядке 1, 6, 4, 3, 2, 5, 1, а в другом — в порядке 1, 2, 4, 5, 6, 3, 1.
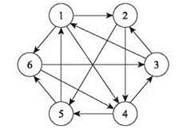
Рис. 8.6. Направленный граф, содержащий гамильтонов цикл
Задача о гамильтоновом цикле формулируется просто:
Содержит ли заданный направленный граф G гамильтонов цикл?
Доказательство NР-полноты задачи о гамильтоновом цикле
Сейчас мы покажем, что обе задачи являются NP-полными. Для этого сначала будет установлена NP-полнота задачи о гамильтоновом цикле, а затем задача о гамильтоновом цикле будет сведена к задаче о коммивояжере.
(8.17) Задача о гамильтоновом цикле является NP-полной.
Доказательство. Сначала мы покажем, что задача о гамильтоновом цикле принадлежит NP. Для направленного графа G = (V, E) сертификатом, подтверждающим наличие решения, является упорядоченный список вершин гамильтонового цикла. По этому списку можно проверить за полиномиальное время, что каждая вершина входит в список ровно один раз, а каждая последовательная пара соединена ребром; эти проверки установят, что упорядочение определяет гамильтонов цикл.
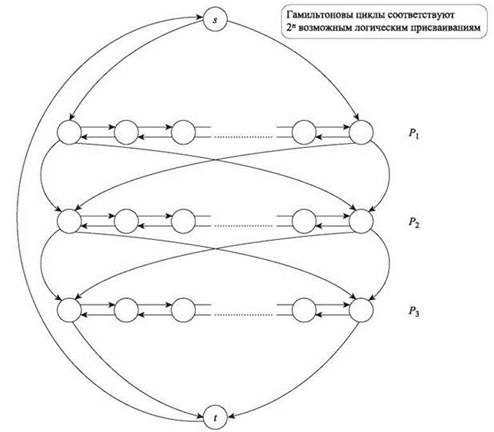
Рис. 8.7. Сведение задачи 3-SAT к задаче о гамильтоновом цикле; часть 1
Покажем, что 3-SAT ≤р Гамильтонов цикл. Почему мы выполняем сведение к 3-SAT? Столкнувшись с задачей о гамильтоновом цикле, мы на самом деле понятия не имеем, что выбрать для сведения; задача достаточно сильно отличается от всех задач, которые мы видели до сих пор, так что реальной основы для выбора нет. В такой ситуации одна из возможных стратегий заключается в возврате к 3-SAT, потому что комбинаторная структура этой задачи очень проста. Конечно, эта стратегия гарантирует по крайней мере некоторый уровень сложности при сведении, потому что переменные и условия необходимо будет выразить на языке графов.
Итак, рассмотрим произвольный экземпляр 3-SAT с переменными х1, ..., xn и условиями C1, ..., Ck. Необходимо показать, как решить эту задачу, если имеется возможность обнаружения гамильтоновых циклов в направленных графах. Как обычно, стоит сосредоточиться на важнейших ингредиентах 3-SAT: значения переменных можно задать по своему усмотрению, и для выполнения каждого условия есть три возможности.
Начнем с описания графа, содержащего 2n разных гамильтоновых циклов, естественно соответствующих возможным 2n логическим присваиваниям значений переменных. После этого мы добавим узлы для моделирования ограничений, накладываемых условиями.
Мы строим n путей P1, ..., Pn, где Pi состоит из узлов vi1, vi2, ..., vib для величины b, которая, как предполагается, немного больше количества условий k; допустим, b = 3k + 3. Существуют ребра из vij к vij+1 и в обратном направлении, от vij+1 к vij. Таким образом, обход Pi может осуществляться “слева направо” от vi1 к vib, или “справа налево”, от vib к vi1.
Эти пути связываются следующим образом: для всех i = 1, 2, ..., n - 1 мы определяем ребра из vi1 в vi+1,1 и в vi+1,b. Также определяются ребра из vib в vi+1,1 и vi+1,b. В граф добавляются два дополнительных узла s и t; мы определяем ребра из s в v11 и v1b; из vn1 и vnb, в t и из t в s.
Построение до настоящего момента изображено на рис. 8.7. Здесь важно задержаться и подумать, как выглядят гамильтоновы циклы на нашем графе. Так как из t выходит только одно ребро, мы знаем, что любой гамильтонов цикл C должен использовать ребро (t, s). После входа в s цикл C может идти по пути P1 либо слева направо, либо справа налево; какое бы направление ни было выбрано, затем он идет по пути P2 либо слева направо, либо справа налево; и т. д., вплоть до завершения Pn и входа в t. Другими словами, существуют ровно 2n разных гамильтоновых циклов, и они соответствуют n независимым выборам направления обхода каждого Pi.
Эта структура естественно моделирует n независимых вариантов присваивания значений переменных x1, ..., xn в экземпляре 3-SAT. Следовательно, каждый гамильтонов цикл будет однозначно идентифицироваться следующим логическим присваиванием: если C проходит Pi слева направо, то xi присваивается 1; в противном случае х. присваивается 0.
Теперь добавим узлы для моделирования условий; экземпляр 3-SAT является выполнимым в том, и только в том случае, если останется хотя бы один гамильтонов цикл. Рассмотрим конкретный пример — условие
C1 = x1 V х2 V х3.
На языке гамильтоновых циклов это условие означает: “Цикл должен проходить Р1 слева направо; или он должен проходить Р2 справа налево; или он должен проходить Р3 слева направо”. Итак, мы добавляем узел с1 (рис. 8.8), который делает именно это. (Некоторые ребра не показаны на рисунке для ясности.) Для некоторого значения l узел с1 имеет ребра из v1l, v2,l+1 и v3l, а также ребра в v1,l+1, v2l и v3,l+1. Следовательно, он легко вставляется в любой гамильтонов цикл, который проходит Р1 слева направо, для чего узел с1 посещается между v1l и v1,l+1; аналогичным образом с1 может быть вставлен в любой гамильтонов цикл, проходящий Р2 справа налево или Р3 слева направо. Он не может быть вставлен в гамильтонов цикл, который не делает ничего из перечисленного.
На более общем уровне узел с. определяется для каждого условия Cj. В каждом пути Рi позиции узлов 3j и 3j + 1 резервируются для переменных, участвующих в условии Сj. Предположим, условие Сi содержит литерал t. Если t = хi, то добавляются ребра (vi,3j, cj) и (cj, vi,3j+1); если ![]() то добавляются ребра (vi,3j+1, cj) и (cj, vi,3j).
то добавляются ребра (vi,3j+1, cj) и (cj, vi,3j).
На этом построение графа G завершается. Далее, в соответствии с приведенной выше общей схемой доказательства ЛР-полноты, мы утверждаем, что экземпляр 3-SAT выполним в том, и только в том случае, если G содержит гамильтонов цикл.
Для начала предположим, что для экземпляра 3-SAT существует выполняющее присваивание; тогда мы определяем гамильтонов цикл в соответствии с приведенным выше неформальным планом. Если х. в выполняющем присваивании задается значение 1, то путь Рi обходится слева направо; в противном случае обход производится справа налево. Для каждого условия Cj, так как оно выполняется вследствие присваивания, будет по крайней мере один путь Рi, в котором обход будет осуществляться в “правильном” направлении относительно узла сj, и его можно вставить в маршрут по ребрам, инцидентным vi,3j и vi,3j+1.
И наоборот, предположим, что в G существует гамильтонов цикл C. Здесь важно заметить следующее: если C входит в узел сj по ребру из vi,3j, то он должен выходить по ребру в vi,3j+1. В противном случае у vi,3j+1 останется только один непосещенный сосед, а именно vi,3j+2, поэтому маршрут не сможет посетить этот узел и сохранить гамильтоново свойство. И симметрично, если маршрут входит из vi,3j+1, он должен немедленно выйти в vi,3j. Следовательно, для каждого узла сj узлы, находящиеся непосредственно до и после сj в цикле C, соединяются ребром e в G; следовательно, если удалить сj из цикла и вставить это ребро e для каждого j, мы получим гамильтонов цикл C' для подграфа G - {с1, ..., сk}. Это наш исходный подграф, до добавления узлов условий; как упоминалось ранее, любой гамильтонов цикл в этом подграфе должен полностью пройти каждый путь Рi в том или ином направлении. Соответственно мы используем C' для определения следующего логического присваивания для экземпляра 3-SAT. Если C' проходит Рi слева направо, то мы задаем хi = 1; в противном случае задается хi = 0. Так как больший цикл Cсмог посетить узел каждого условия сj, по крайней мере один из путей проходился в “правильном” направлении относительно узла сj, поэтому с определенным нами присваиванием выполняются все условия.
Установлено, что экземпляр 3-SAT выполним в том, и только в том случае, если G содержит гамильтонов цикл; на этом наше доказательство завершается.

Рис. 8.8. Сведение задачи 3-SAT к задаче о гамильтоновом цикле; часть 2
Доказательство NР-полноты задачи коммивояжера
Вооружившись базовым результатом сложности задачи о гамильтоновом цикле, мы можем перейти к демонстрации сложности задачи коммивояжера.
(8.18) Задача коммивояжера является NP-полной.
Доказательство. Легко увидеть, что задача коммивояжера принадлежит NP: сертификат представляет собой перестановку городов, а сертифицирующий алгоритм проверяет, что длина соответствующего маршрута не превышает заданной границы.
Теперь покажем, что Гамильтонов цикл ≤Р Коммивояжер. Для заданного направленного графа G = (V, E) определяется следующий экземпляр задачи коммивояжера. Каждому узлу vi графа Gсоответствует город v'i. Мы определяем d(v'i, v'j) равным 1, если в G существует ребро (vi, vj), и 2 — в противном случае.
Утверждается, что G содержит гамильтонов цикл в том, и только в том случае, если в экземпляре задачи коммивояжера имеется маршрут длины не более n. Если G содержит гамильтонов цикл, то упорядочение соответствующих городов определяет маршрут длины n. И наоборот, предположим, что существует маршрут длины не более n. Выражение для длины маршрута представляет собой сумму n слагаемых, каждое из которых не менее 1; следовательно, все слагаемые должны быть равны 1. Следовательно, каждая пара узлов G, соответствующих соседним городам маршрута, должна быть соединена ребром; из этого следует, что упорядочение соответствующих узлов должно образовать гамильтонов цикл. ■
Обратите внимание: возможная асимметричность расстояний в задаче коммивояжера (d(v'i, v'j) ≠ d(v'j, v'i)) сыграла важнейшую роль; так как граф из экземпляра задачи о гамильтоновом цикле является направленным, наше сведение дало экземпляр задачи коммивояжера с асимметричными расстояниями.
Собственно, аналогия задачи о гамильтоновом цикле для ненаправленных графов также является ЖР-полной; хотя здесь доказательство не приводится, оно строится на относительно несложном сведении от задачи для направленного графа. При использовании задачи о гамильтоновом цикле в ненаправленном графе точная аналогия (8.18) может использоваться для доказательства ЖР-полноты задачи коммивояжера с симметричными расстояниями.
Конечно, в самом известном частным случае задачи коммивояжера расстояния определяются множеством из п точек на плоскости. Задачу о гамильтоновом цикле можно свести и к этому частному случаю, хотя сделать это намного сложнее.
Расширения: задача о гамильтоновом пути
Иногда бывает полезно рассмотреть разновидность задачи о гамильтоновом цикле, в которой не обязательно возвращаться к начальной точке. Для заданного направленного графа G = (V, E) путь Р в G называется гамильтоновым путем, если каждая вершине входит в него ровно один раз. (Путь может начинаться с любого узла и заканчиваться на любом узле при условии соблюдения указанного ограничения.) Такой путь состоит из разных узлов vi1, vi2, ..., и vin, в определенном порядке, образующих все множество вершин V; в отличие от гамильтонова цикла, наличие ребра из vin обратно в vi1 не обязательно. Задача о гамильтоновом пути формулируется так:
Содержит ли заданный направленный граф G гамильтонов путь?
Используя сложность задача о гамильтоновом цикле, мы покажем следующее.
(8.19) Задача о гамильтоновом пути является ЖР-полной.
Доказательство. Прежде всего задача о гамильтоновом пути принадлежит ЖР: сертификатом может быть путь в G, а сертифицирующий алгоритм проверяет, что он действительно является путем и каждый узел входит в него ровно один раз.
Один из способов демонстрации ХР-полноты задачи о гамильтоновом пути заключается в сведении от 3-SAT, почти идентичного тому, которое мы использовали для задачи о гамильтоновом цикле: мы строим граф, изображенный на рис. 8.7, с тем отличием, что в него не включается ребро из t в s. Если в измененном графе нет ни одного гамильтонова пути, он должен начинаться в s (так как s не имеет входящих ребер) и завершаться в t (так как t не имеет выходящих ребер). Одно изменение позволяет более или менее дословно применить аргумент, использованный в сведении гамильтонова цикла, для обоснования того, что выполняющее присваивание для экземпляра 3-SAT существует в том, и только в том случае, если существует гамильтонов путь.
Альтернативный способ демонстрации ХР-полноты гамильтонова пути основан на доказательстве Гамильтонов цикл ≤Р Гамильтонов путь. Для заданного экземпляра задачи о гамильтоновом цикле, заданном направленным графом G, строится граф G' по следующим правилам: мы выбираем произвольный узел v в G и заменяем его двумя новыми узлами v' и v''. Все ребра, выходившие из v в G, теперь выходят из v'; а все ребра, входившие в v в G, теперь входят в v''. А точнее, каждое ребро (v, w) в G заменяется ребром (v', w); а каждое ребро (u, v) в Gзаменяется ребром (u, v''). На этом построение G' завершается.
Утверждается, что G' содержит гамильтонов путь в том, и только в том случае, если G содержит гамильтонов цикл. Предположим, что C — гамильтонов цикл в G; рассмотрим обход этого цикла, начиная и заканчивая в узле v. Легко увидеть, что то же упорядочение узлов образует в G' гамильтонов путь, который начинается с v' и завершается в v''. И наоборот, предположим, что Р — гамильтонов путь в G'; очевидно, он должен начинаться в v' (так как v' не содержит входящих ребер) и заканчиваться в v" (так как v" не содержит выходящих ребер). Если заменить v' и v" на v, то это упорядочение узлов образует гамильтонов цикл в G.