Обзор типичных вариантов времени выполнения - Основы анализа алгоритмов

Когда вы пытаетесь проанализировать новый алгоритм, полезно иметь хотя бы приблизительное представление о “спектре” разных вариантов времени выполнения. В самом деле, некоторые типы анализа встречаются часто, и когда вы сталкиваетесь с распространенными границами времени выполнения вида O(n), O(n log n) или O(n²), часто это объясняется одной из немногочисленных, но хорошо узнаваемых причин. Для начала мы приведем сводку типичных границ времени выполнения, а также типичные аналитические методы, приводящие к ним.

Ранее мы уже говорили о том, что у многих задач существует естественное “пространство поиска” — совокупность всех возможных решений, а также упоминали, что объединяющей темой в проектировании алгоритмов является поиск алгоритмов, превосходящих по эффективности перебор пространства поиска методом “грубой силы”. Соответственно, когда вы беретесь за новую задачу, часто бывает полезно рассматривать два вида границ: для времени выполнения, которое вы рассчитываете достичь, и для размера естественного пространства поиска задачи (а следовательно, для времени выполнения алгоритма методом “грубой силы”). Обсуждение вариантов времени выполнения в этом разделе часто будет начинаться с анализа алгоритма “грубой силы”, который поможет разобраться в особенностях задачи. Большая часть книги будет посвящена тому, как добиться повышения быстродействия по сравнению с такими алгоритмами.

Линейное время

Алгоритм с временем O(n), или линейным временем, обладает одним очень естественным свойством: его время выполнения не превышает размера входных данных умноженного на константу. Чтобы обеспечить линейное время выполнения, проще всего обработать входные данные за один проход, с постоянными затратами времени на обработку каждого элемента. Другие алгоритмы достигают линейной границы времени выполнения по менее очевидным причинам. Чтобы дать представление о некоторых принципах анализа, мы рассмотрим два простых алгоритма с линейным временем выполнения.

Вычисление максимума

Вычисление максимума из n чисел может быть выполнено классическим “однопроходным” методом. Допустим, числа поступают на вход в виде списка или массива. Числа a₁, a₂, ... обрабатываются последовательно, с сохранением текущего максимума во время выполнения. Каждое очередное число а_i сравнивается с текущим максимумом, и если оно больше, текущий максимум заменяется значением a_i.

При таком решении для каждого элемента выполняется постоянный объем работы, а общее время выполнения составляет O(n).

Иногда необходимость применения однопроходных алгоритмов объясняется ограничениями приложения: например, алгоритм, работающий на высокоскоростном коммутаторе в Интернете, “видит” проходящий мимо него поток пакетов и может выполнять любые необходимые вычисления с проходящими пакетами. При этом для каждого пакета выполняется ограниченный объем вычислительной работы, и поток не может сохраняться для перебора в будущем. Для изучения этой модели вычислений были разработаны две специализированные подобласти: онлайновые алгоритмы и алгоритмы потоков данных.

Слияние двух отсортированных списков

Часто алгоритмы обладают временем выполнения O(n) по более сложным причинам. Сейчас будет рассмотрен алгоритм слияния двух отсортированных списков, который немного выходит за рамки “однопроходной” схемы, но при этом все равно обладает линейным временем.

Допустим, имеются два списка, каждый из которых состоит из n чисел: a₁, a₂, ..., a_n и b₁, b₂, ..., b_n. Оба списка уже отсортированы по возрастанию. Требуется объединить их в один список c₁, c₂, ..., c_2n, который также упорядочен по возрастанию. Например, при слиянии списков 2, 3, 11, 19 и 4, 9, 16, 25 должен быть получен список 2, 3, 4, 9, 11, 16, 19, 25.

Для этого можно было бы просто свалить оба списка в одну кучу, игнорируя тот факт, что они уже упорядочены по возрастанию, и запустить алгоритм сортировки. Но такое решение явно неэффективно: нужно использовать существующий порядок элементов во входных данных. Чтобы спроектировать более совершенный алгоритм, подумайте, как бы вы выполняли слияние двух списков вручную. Допустим, имеются две стопки карточек с числами, уже разложенные по возрастанию, и вы хотите получить одну стопку со всеми карточками. Взглянув на верхнюю карточку каждой стопки, вы знаете, что карточка с меньшим числом должна предшествовать второй в выходной стопке; вы снимаете карточку, кладете ее в выходную стопку и повторяете процедуру для полученных стопок.

Иначе говоря, имеется следующий алгоритм:

Схема работы этого алгоритма изображена на рис. 2.2.

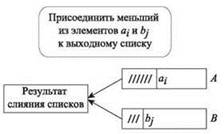
Рис. 2.2. Чтобы выполнить слияние двух списков, мы в цикле извлекаем меньший из начальных элементов двух списков и присоединяем его к выходному списку

Утверждение о линейной границе времени выполнения хотелось бы подтвердить тем же аргументом, который использовался для алгоритма поиска максимума: “Для каждого элемента выполняется постоянный объем работы, поэтому общее время выполнения составляет O(n)”. Но на самом деле нельзя утверждать, что для каждого элемента выполняется постоянная работа. Допустим, n — четное число; рассмотрим списки A = 1, 3, 5, ..., 2n - 1 и B = n, n + 2, n + 4, ..., 3n - 2. Число b₁ в начале списка B будет находиться в начале списка для n/2 итераций при повторном выборе элементов из A, а следовательно, будет участвовать в Ω(n) сравнениях. Каждый элемент может быть задействован максимум в O(n) сравнениях (в худшем случае он сравнивается с каждым элементом другого списка), и при суммировании по всем элементам будет получена граница времени выполнения O(n²). Эта граница верна, но можно существенно усилить ее точность.

Самый наглядный аргумент — ограничение количества итераций цикла “Пока” по “учетной” схеме. Предположим, для каждого элемента при выборе и добавлении его в выходной список взимается оплата. За каждый элемент платить придется только один раз, так как оплаченный элемент добавляется в выходной список и уже никогда не рассматривается алгоритмом. Всего существуют 2n элементов, и каждая итерация оплачивается некоторым элементом, поэтому количество итераций не может быть больше 2n. В каждой итерации используется постоянный объем работы, поэтому общее время выполнения имеет границу O(n), как и требовалось.

Хотя алгоритм слияния перебирает свои входные списки по порядку, “чередование” последовательности обработки списков требует применения чуть более сложного анализа времени выполнения. В главе 3 будут представлены алгоритмы с линейным временем для графов, которые требуют еще более сложного процесса управления: для каждого узла и ребра графа тратится постоянное время, но порядок обработки узлов и ребер зависит от структуры графа.

Время O(n log n)

Время O(n log n) тоже встречается очень часто, и в главе 5 будет представлена одна из главных причин его распространенности: это время выполнения любого алгоритма, который разбивает входные данные на две части одинакового размера, рекурсивно обрабатывает каждую часть, а затем объединяет два решения за линейное время.

Пожалуй, классическим примером задачи, которая может решаться подобным образом, является сортировка. Так, алгоритм сортировки слиянием разбивает входной набор чисел на две части одинакового размера, рекурсивно сортирует каждую часть, а затем объединяет две отсортированные половины в один отсортированный выходной список. Только что было показано, что слияние может быть выполнено за линейное время; в главе 5 мы обсудим анализ рекурсии для получения границы O(n log n) в общем времени выполнения.

Время O(n log n) также часто встречается просто из-за того, что во многих алгоритмах самым затратным шагом является сортировка входных данных. Допустим, имеется набор из n временных меток x₁, x₂, ..., x_n поступления копий файлов на сервер, и нам хотелось бы определить наибольший интервал между первой и последней из этих временных меток, в течение которого не поступило ни одной копии файла. Простейшее решение этой задачи — отсортировать временные метки x₁, x₂, ..., x_n, а затем обработать их в порядке сортировки и вычислить интервалы между каждыми двумя соседними числами. Наибольший из этих интервалов дает желаемый результат. Этот алгоритм требует времени O(n log n) на сортировку чисел, с последующим постоянным объемом работы для каждого числа в порядке перебора. Другими словами, после сортировки вся оставшаяся работа следует основному сценарию линейного времени, который рассматривался ранее.

Квадратичное время

Типичная задача: заданы n точек на плоскости, определяемых координатами (x,у); требуется найти пару точек, расположенных ближе всего друг к другу. Естественный алгоритм “грубой силы” для такой задачи перебирает все пары точек, вычисляет расстояния между каждой парой, а затем выбирает пару, для которой это расстояние окажется наименьшим.

Какое время выполнения обеспечит такой алгоритм? Количество пар точек равно а поскольку эта величина ограничивается 1/2n², она имеет границу O(n²). Проще говоря, количество пар ограничивается O(n²) потому, что количество способов выбора первого элемента пары (не больше n) умножается на количество способов выбора второго элемента пары (тоже не больше n). Расстояние между точками (x_i, у_i) и (x_j, у_j) вычисляется по формуле за постоянное время, так что общее время выполнения ограничивается O(n²).

В этом примере представлена очень распространенная ситуация, в которой встречается время выполнения O(n²): перебор всех пар входных элементов с постоянными затратами времени на каждую пару.

Квадратичное время так же естественно возникает в парах вложенных циклов: алгоритм состоит из цикла с O(n) итерациями, и каждая итерация цикла запускает внутренний цикл с временем O(n). Произведение двух множителей n дает искомое время выполнения.

Эквивалентная запись алгоритм поиска ближайшей пары точек методом “грубой силы” с использованием двух вложенных циклов выглядит так:

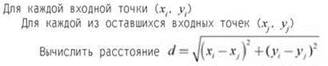
Обратите внимание: “внутренний” цикл по (x_j, у_j) состоит из O(n) итераций, каждая из которых выполняется за постоянное время, и “внешний” цикл по (x_i, у_i) состоит из O(n) итераций, каждая из которых один раз запускает внутренний цикл.

Важно заметить, что алгоритм, рассматриваемый нами для задачи ближайшей пары точек, в действительности относится к методам “грубой силы”: естественное пространство поиска этой задачи имеет размер O(n²), и мы всего лишь перебираем его. На первый взгляд может показаться, что в квадратичном времени есть некая неизбежность — ведь нам все равно придется перебрать все расстояния, не так ли? — но в действительности это всего лишь иллюзия. В главе 5 будет описан очень остроумный алгоритм для поиска ближайшей пары точек на плоскости за время всего лишь O(n log n), а в главе 13 мы покажем, как применение рандомизации сокращает время выполнения до O(n).

Кубическое время

Более сложные группы вложенных циклов часто приводят к появлению алгоритмов, выполняемых за время O(n³). Для примера рассмотрим следующую задачу. Имеются множества S₁, S₂, ..., S_n, каждое из которых является подмножеством {1, 2, ..., n}; требуется узнать, можно ли найти среди этих множеств непересекающуюся пару (то есть два множества, не имеющих общих элементов).

Какое время потребуется для решения этой задачи? Предположим, каждое множество S_i представлено таким образом, что элементы S_i могут быть обработаны с постоянными затратами времени на элемент, а проверка того, входит ли заданное число p в S_i, также выполняется за постоянное время. Ниже описано наиболее прямолинейное решение задачи.

Алгоритм выглядит конкретно, но чтобы оценить его время выполнения, полезно преобразовать его (по крайней мере концептуально) в три вложенных цикла.

Каждое из множеств имеет максимальный размер п, поэтому внутренний цикл выполняется за время O(n). Перебор множеств S_j требует O(n) итераций внутреннего цикла, а перебор множеств S_iтребует O(n) итераций внешнего цикла. Перемножая эти три множителя, мы получаем время выполнения O(n³).

Для этой задачи существуют алгоритмы, улучшающие время выполнения O(n³), но они достаточно сложны. Более того, не очевидно, дают ли эти улучшенные алгоритмы практический выигрыш при входных данных разумного размера.

Время O(n^k)

По тем же соображениям, по которым мы пришли к времени выполнения O(n²), применяя алгоритм “грубой силы” ко всем парам множества из n элементов, можно получить время выполнения O(n^k) для любой константы k при переборе всех подмножеств размера k.

Для примера возьмем задачу поиска независимого множества в графе, упоминавшуюся в главе 1. Напомним, что множество узлов называется независимым, если никакие два узла не соединяются ребром. А теперь допустим, что для некоторой константы k мы хотим узнать, содержит ли входной граф G с n узлами независимое множество размера k. Естественный алгоритм “грубой силы” для этой задачи перебирает все подмножества из k узлов, и для каждого подмножества S проверяет существование ребра, соединяющего любые два узла из S. На псевдокоде это выглядит так:

Чтобы понять время выполнения этого алгоритма, необходимо учесть два фактора. Во-первых, общее количество к-элементных подмножеств в множестве из n элементов равно

Так как к считается постоянной величиной, эта величина имеет порядок O(n^k). Следовательно, внешний цикл алгоритма, перебирающий все k-элементные подмножества n узлов графа, выполняется за O(n^k) итераций.

Внутри цикла необходимо проверить, образует ли заданное множество S из k узлов независимое множество. Согласно определению независимого множества, необходимо для каждой пары узлов проверить, соединяются ли они ребром. Это типичная задача поиска по парам, которая, как было показано ранее при обсуждении квадратичного времени выполнения, требует проверки то есть O(k²) пар при постоянных затратах времени на каждую пару.

Итак, общее время выполнения равно O(k²n^k). Так как к считается константой, а константы в записи O(∙) могут опускаться, это время выполнения можно записать в виде O(n^k).

Поиск независимых множеств — типичный пример задачи, которая считается вычислительно сложной. В частности, считается, что никакой алгоритм поиска независимого множества из к узлов в произвольных графах не может избежать зависимости от к в показателе степени. Но, как будет показано в главе 10 в контексте похожей задачи, даже если согласиться с тем, что поиск методом “грубой силы” по k-элементным подмножествам неизбежен, существуют разные варианты реализации, приводящие к существенным различиям в эффективности вычислений.

За границами полиномиального времени

Задача поиска независимого множества подводит нас к границе области времен выполнения, растущих быстрее любого полиномиального времени. В частности, на практике очень часто встречаются границы 2ⁿ и n!; сейчас мы обсудим, почему это происходит.

Предположим, для некоторого графа нужно найти независимое множество максимального размера (вместо того, чтобы проверять сам факт существования при заданном количестве узлов). До настоящего времени не известны никакие алгоритмы, обеспечивающие заметный выигрыш по сравнению с поиском методом “грубой силы”, который в данном случае выглядит так:

Этот алгоритм очень похож на алгоритм “грубой силы” для независимых множеств из k узлов, однако на этот раз перебор ведется по всем подмножествам графа. Общее количество подмножеств n-элементного множества равно 2ⁿ, поэтому внешний цикл алгоритма будет выполнен в 2ⁿ итерациях при переборе всех этих подмножеств. Внутри цикла перебираются все пары из множества S, которое может содержать до n узлов, так что каждая итерация цикла выполняется за максимальное время O(n²). Перемножая эти два значения, мы получаем время выполнения O(n²2ⁿ).

Как видите, граница 2ⁿ естественным образом возникает в алгоритмах поиска, которые должны рассматривать все возможные подмножества. Похоже, в задаче поиска независимого множества такая (или по крайней мере близкая) неэффективность неизбежна; но важно помнить, что пространство поиска с размером 2ⁿ встречается во многих задачах, и достаточно часто удается найти высокоэффективный алгоритм с полиномиальным временем выполнения. Например, алгоритм поиска методом “грубой силы” для задачи интервального планирования, упоминавшейся в главе 1, очень похож на представленный выше: мы опробуем все подмножества интервалов и находим наибольшее подмножество без перекрытий. Однако в задаче интервального планирования, в отличие от задачи поиска независимого множества, оптимальное решение может быть найдено за время O(n log n) (см. главу 4). Такого рода дихотомия часто встречается при изучении алгоритмов: два алгоритма имеют внешне похожие пространства поиска, но в одном случае алгоритм поиска методом “грубой силы” удается обойти, а в другом нет.

Функция n! растет еще быстрее, чем 2ⁿ, поэтому в качестве границы производительности алгоритма она выглядит еще более угрожающе. Пространства поиска размера n! обычно встречаются по одной из двух причин. Во-первых, n! — количество комбинаций из n элементов с n другими элементами, например количество возможных идеальных паросочетаний n мужчин с n женщинами в задаче поиска устойчивых паросочетаний. У первого мужчины может быть n вариантов пары; после исключения выбранного варианта для второго мужчины остается n - 1 вариантов; после исключения этих двух вариантов для третьего остается n - 2 вариантов, и т. д. Перемножая все эти количества вариантов, получаем n(n - 1) (n - 2) ... (2)(1) = n!

Несмотря на огромное количество возможных решений, нам удалось решить задачу устойчивых паросочетаний за O(n²) итераций алгоритма с предложениями. В главе 7 аналогичное явление встретится нам в контексте задачи двудольных паросочетаний, о которой говорилось ранее; если на каждой стороне двудольного графа находятся n узлов, существуют n! возможных комбинаций. Однако достаточно хитроумный алгоритм поиска позволит найти наибольшее двудольное паросочетание за время O(n³).

Функция n! также встречается в задачах, в которых пространство поиска состоит из всех способов упорядочения n элементов. Типичным представителем этого направления является задача коммивояжера: имеется множество из n городов и расстояния между всеми парами, как выглядит самый короткий маршрут с посещением всех городов? Предполагается, что коммивояжер начинает и заканчивает поездку в первом городе, так что суть задачи сводится к неявному поиску по всем вариантам упорядочения остальных n - 1 городов, что ведет к пространству поиска размером (n - 1)!. В главе 8 будет показано, что задача коммивояжера, как и задача независимых множеств, относится к классу ЖР-полных задач; как предполагается, она не имеет эффективного решения.

Сублинейное время

Наконец, в некоторых ситуациях встречается время выполнения, асимптотически меньшее линейного. Так как для простого чтения входных данных потребуется линейное время, такие ситуации обычно встречаются в модели вычислений с косвенными “проверками” входных данных вместо их полного чтения, а целью является минимизация количества необходимых проверок.

Пожалуй, самым известным примером такого рода является алгоритм бинарного поиска. Имеется отсортированный массив A из n чисел; требуется определить, принадлежит ли массиву заданное число р. Конечно, задачу можно решить чтением всего массива, но нам хотелось бы действовать намного более эффективно — проверять отдельные элементы, используя факт сортировки массива. Алгоритм проверяет средний элемент A и получает его значение (допустим, q), после чего q сравнивается с р. Если q = р, поиск завершается. Если q > р, то значение р может находиться только в нижней половине A; с этого момента верхняя половина A игнорируется, а процедура поиска рекурсивно применяется к нижней половине. Если же q < р, то применяются аналогичные рассуждения, а поиск рекурсивно продолжается в верхней половине A.

Суть в том, что на каждом шаге существует некая область A, в которой может находиться р; при каждой проверке размер этой области уменьшается вдвое. Каким же будет размер “активной” области А после к проверок? Начальный размер равен n, поэтому после к проверок он будет равен максимум

Учитывая это обстоятельство, сколько шагов понадобится для сокращения активной области до постоянного размера? Значение k должно быть достаточно большим, чтобы а для этого мы можем выбрать k = log₂n. Таким образом, при k = log₂ n размер активной области сокращается до константы; в этой точке рекурсия прекращается, и поиск в оставшейся части массива может быть проведен за постоянное время.

Следовательно, бинарный поиск из-за последовательного сокращения области поиска имеет время выполнения O(log n). В общем случае временная граница O(log n) часто встречается в алгоритмах, выполняющих постоянный объем работы для отсечения постоянной доли входных данных. Принципиально здесь то, что O(log n) таких итераций сократят входные данные до постоянного размера, при котором задача обычно может быть решена напрямую.