Построение древовидной декомпозиции - Расширение пределов разрешимости

В предыдущем разделе были представлены концепции декомпозиции графа в дерево и древовидной ширины, а также рассмотрен канонический пример решения NР-сложной задачи для графов с ограниченной древовидной шириной.

Задача

В нашем алгоритмическом использовании древовидной ширины все еще не хватает одной важной составляющей. Пока что мы просто предоставили алгоритм для нахождения независимого множества с максимальным весом для графа G для заданной древовидной декомпозиции G с малой шириной. А если граф G просто появляется “на ровном месте” и никто не побеспокоился предоставить хорошую древовидную декомпозицию? Можно ли вычислить ее самостоятельно, а затем перейти к алгоритму динамического программирования?

В общих чертах — да, можно, но не без проблем. Сначала необходимо предупредить о том, что для заданного графа G определение его древовидной ширины является ЛР-сложной задачей. Впрочем, все не так плохо, потому что нас интересуют только графы, для которых древовидная ширина является малой константой. А в этом случае алгоритм описывается со следующей гарантией: для заданного графа G с древовидной шириной менее w он строит декомпозицию G в дерево с шириной менее 4w за время O(f(w) ∙ mn), где m и n — количество ребер и узлов в G, а f(∙) — функция, зависящая только от w. Итак, по сути при небольшой древовидной ширине существует достаточно быстрый способ построения древовидной декомпозиции с почти минимально возможной шириной.

Разработка и анализ алгоритма

Первым шагом при разработке алгоритма для этой задачи является выявление разумного “препятствия” к тому, чтобы граф G имел малую древовидную ширину. Другими словами, когда мы пытаемся построить древовидную декомпозицию малой ширины для G = (V, E), может ли существовать некая “локальная” структура, обнаружение которой укажет на то, что древовидная ширина на самом деле должна быть большой?

Оказывается, следующая идея помогает найти такое препятствие. Во-первых, два множества Y, Z ⊆ V с одинаковым размером называются разделимыми, если некоторое строго меньшее множество может полностью нарушить их связность, а именно если существует такое множество S ⊆ V, что |S| < |Y| = |Z| и не существует пути от Y - S к Z - S в G - S. (В этом определении Y и Z не обязаны быть непересекающимися.) Далее множество X узлов в G будет называться w-связным, если |X| ≥ w и X не содержит разделяемые подмножества Y и Z, такие что |Y| = |Z| ≤ w.

Для последующего алгоритмического применения w-связных множеств обратите внимание на следующий факт:

(10.19) Пусть граф G = (V, E) имеет m ребер, X — множество из k узлов в G, а w ≤ k — заданный параметр. Тогда можно определить, является ли множество X w-связным, за время O(f(k) ∙ m), где f(∙) зависит только от k. Более того, если множество X не является w-связным, доказательство этого факта можно вернуть в форме множеств Y, Z ⊆ X и S ⊆ V, для которых |S| < |Y| = |Z| ≤ w и не существует пути от Y - S к Z - S в G - S.

Доказательство. Нужно решить, содержит ли X разделимые подмножества Y и Z, для которых |Y| = |Z| ≤ w. Сначала можно перебрать все пары достаточно малых подмножеств Y и Z; так как X имеет только 2^k подмножеств, количество таких пар не превышает 4^k.

Затем для каждой пары подмножеств Y, Z необходимо определить, являются ли эти множества разделимыми. Пусть l = |Y| = |Z| ≤ w. Но ситуация точно совпадает с теоремой о максимальном потоке и минимальном разрезе для ненаправленного графа с пропускными способностями узлов: Y и Z разделимы в том, и только в том случае, если не существуют l путей, не пересекающихся по узлам, один конец которых находится в Y, а другой в Z. (За версией теоремы о максимальном потоке с пропускными способностями узлов обращайтесь к упражнению 13 главы 7.) Чтобы определить, существуют ли такие пути, можно воспользоваться алгоритмом для потока с (единичными) пропускными способностями узлов; это занимает время O(l m). ■

W-связное множество можно представить себе как “тесно сплетенное” — у него нет двух малых частей, которые можно легко отделить друг от друга. В то же время декомпозиция производит разбивку графа с использованием очень малых разделителей; интуитивно понятно, что эти две структуры могут рассматриваться как противоположности.

(10.20) Если граф G содержит (w + 1)-связное множество с размером не менее 3w, то древовидная ширина G не менее w.

Доказательство. Предположим от обратного, что граф G имеет (w + 1)-связное множество X с размером не менее 3w, а также для него существует декомпозиция (T, {V_t}) с шириной менее w; иначе говоря, размер каждого фрагмента V_t не превышает w. Также можно считать, что декомпозиция (T, {V_t}) не содержит избыточности.

Идея доказательства заключается в том, чтобы найти фрагмент V_t, расположенный “по центру” в отношении X, чтобы при удалении из G некоторой части V_t одно малое подмножество Xотделялось от другого. Так как размер V_t не превышает w, это будет противоречить нашему предположению о том, что X является (w + 1)-связным.

Как же найти этот фрагмент V_t? Сначала мы размещаем корень дерева Т в узле r; как и прежде, обозначим T_t поддерево с корнем в узле t и запишем G_t для Пусть теперь t — узел, находящийся как можно дальше от корня r, с тем ограничением, что G_t содержит более 2w узлов X.

Очевидно, t не является листом (в противном случае подграф G_t содержал бы не более w узлов X; обозначим t₁, ..., t_d дочерние узлы t. Обратите внимание: так как каждый узел t_i находится от t на большем расстоянии, чем корень, каждый подграф содержит не более 2w узлов из X. Если существует дочерний узел t_i, для которого содержит не менее w узлов из X, мы можем определить Y как w узлов X, принадлежащих a Z — как w узлов X, принадлежащих Так как декомпозиция (Т, {V_t}) не имеет избыточности, размер не превышает w - 1; но согласно (10.14), удаление S приводит к отделению Y – S OT Z - S. ЭТО противоречит нашему предположению о том, что множество X является (w + 1)-связным.

Соответственно мы рассматриваем случай, в котором нет такого дочернего узла t_i, для которого содержит не менее w узлов из X; структура графа в этом случае выглядит примерно так, как показано на рис. 10.9. Мы начинаем с множества узлов объединяем его с затем и т. д., пока впервые не получим множество узлов, содержащее более w членов X. Очевидно, это уже случится к тому моменту, когда мы доберемся до потому что G_t содержит более 2^w узлов из X и не более w из них могут принадлежать V_t. Допустим, процесс объединения впервые дает более w членов X при достижении индекса i ≤ d. Обозначим W множество узлов в подграфах Согласно условию завершения |W ∩ X| > w. Но поскольку содержит менее wузлов X, также имеем |W ∩ X| < 2w. Следовательно, мы можем определить Y как w + 1 узлов X, принадлежащих W, а Z — как w + 1 узлов X, принадлежащих V - W. Согласно (10.13) фрагмент V_t теперь является множеством с размером, не превышающим w, удаление которого приводит к отделению Y - V_t от Z - V_t. И снова это противоречит предположению о том, что множество X является (w + 1)-связным, завершая наше доказательство. ■

Рис. 10.9. Последний шаг доказательства (10.20)

Алгоритм поиска декомпозиции с малой древовидной шириной

Продолжая развивать эти идеи, мы приведем жадный алгоритм для построения древовидной декомпозиции низкой ширины. Алгоритм не будет точно определять древовидную ширину входного графа G = (V, E); вместо этого он по заданному параметру w либо строит декомпозицию ширины менее 4w, либо обнаруживает (w + 1)-связное множество с размером не менее 3w. В последнем случае это составляет доказательство того, что древовидная ширина G не менее w согласно (10.20); итак, наш алгоритм, по сути, способен сузить фактическую древовидную ширину G до 4 раз. Как упоминалось ранее, время выполнения определяется в форме O(f(w) ∙ mn), где m и n — количество ребер и узлов G, а f(∙) зависит только от w.

С некоторым опытом работы с декомпозициями можно представить себе, что может потребоваться для построения декомпозиции для произвольного входного графа G. На верхнем уровне этот процесс изображен на рис. 10.10. Наша цель — заставить G распасться на древовидные части; декомпозиция начинается с размещения первого фрагмента V_t в любом месте. Если повезет, G - V_t состоит из нескольких изолированных компонент; мы рекурсивно заходим в каждую компоненту и размещаем в ней фрагмент так, чтобы он частично перекрывал уже определенный фрагмент V_t. Мы надеемся, что эти новые фрагменты приведут к дальнейшему разбиению графа; этот процесс продолжается далее. Ключевую роль в работе этого алгоритма играет следующий факт: если в какой-то момент мы окажемся в тупике и наши малые множества не приведут к дальнейшему разбиению графа, можно будет извлечь большое (w + 1)-связное множество, которое докажет, что древовидная ширина на самом деле была большой.

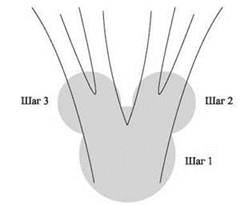
Рис. 10.10. Схематичное представление первых трех шагов в построении декомпозиции графа. Так как каждый шаг порождает новый фрагмент, нашей целью является разбиение остатка графа на несвязанные компоненты для применения дальнейших итераций алгоритма

Все эти объяснения выглядят несколько туманно, но реальный алгоритм следует им точнее, чем можно было ожидать. Мы начинаем с предположения о том, что не существует (w + 1)-связного множества с размером не менее 3w; наш алгоритм строит декомпозицию, если условие выполняется; в противном случае его выполнение можно завершить с доказательством того, что древовидная ширина G не менее w. Дерево декомпозиции T и фрагменты V_t увеличиваются по жадному правилу. На каждой промежуточной стадии алгоритма сохраняется свойство частичной декомпозиции: если U ⊆ V — множество узлов G, принадлежащих минимум одному из уже построенных фрагментов, то текущее дерево T и фрагменты V_t должны образовать древовидную декомпозицию подграфа G, порожденного U. Мы определяем ширину частичной декомпозиции (по аналогии с определением ширины декомпозиции в дерево) на 1 меньше максимального размера фрагмента. Это означает, что для достижения цели — ширины менее 4w — достаточно убедиться в том, что размер всех фрагментов не превышает 4w. Если C — компонента связности G-U, то u ∈ U называется соседом C, если существует некоторый узел v ∈ C, соединенный ребром с u. Для работы алгоритма важно не просто поддерживать частичную декомпозицию с шириной менее 4w, но и обеспечить постоянное соблюдение следующего инварианта:

(*) На любой стадии выполнения алгоритма каждая компонента C подграфа G-U имеет не более 3w соседей, и существует единственный фрагмент V_t, который содержит их все.

Чем этот инвариант так полезен? Тем, что он позволит нам добавить новый узел s в T и нарастить новый фрагмент V_s в компоненте C с уверенностью в том, что s может быть листом, “свисающим” с t в большей частичной декомпозиции.

Более того, (*) требует, чтобы соседей было не более 3w, при том что мы пытаемся построить декомпозицию с шириной менее 4w; дополнительное w дает новому фрагменту “свободное место” для расширения при перемещении в C.

А теперь мы опишем, как добавить новый узел и новый фрагмент так, чтобы поддерживалась частичная декомпозиция дерева, не нарушался инвариант (*), а множество U строго увеличилось. При этом алгоритм продвинется по крайней мере на один узел, а следовательно, завершится не более чем за n итераций древовидной декомпозицией всего графа G.

Пусть C — любая компонента G - U, X — множество соседей U, а V_t — фрагмент, который, как гарантирует (*), содержит все множество X. Мы знаем (снова из (*)), что X содержит не более 3wузлов. Если X содержит строго меньше 3w узлов, можно продвинуться вперед немедленно: для любого узла v ∈ C определяется новый фрагмент V_s = X U {v}, а s становится листом t. Так как концы всех ребер из v в U принадлежат X, легко убедиться в том, что мы имеем частичную декомпозицию, подчиняющуюся (*), а множество U увеличилось.

Предположим, X содержит ровно 3w узлов. В этом случае дальнейшее уже не столь очевидно; например, если попытаться создать новый фрагмент произвольным добавлением узла v ∈ C в X, может получиться компонента из C - {v} (в том числе и все множество C - {v}), множество соседей которой включает все 3w + 1 узлов X U {v}, а это нарушит (*).

Простого выхода не существует; прежде всего, граф G может и не иметь древовидной декомпозиции с малой шириной. А значит, именно здесь стоит задаться вопросом, создает ли X настоящее препятствие для декомпозиции или нет: мы проверяем, является ли X (w + 1)-связным множеством. Согласно (10.19), ответ может быть получен за время O(f(w) ∙ m), так как |X| = 3w. Если окажется, что множество X является (w + 1)-связным, то дело сделано; выполнение можно прервать с заключением о том, что G имеет древовидную ширину не менее w, что является одним из допустимых результатов алгоритма. С другой стороны, если множество X не является (w + 1)-связным, то мы получаем Y, Z ⊆ X и S ⊆ V, такие что |S| < |Y| = |Z| ≤ w + 1, и не существует пути от Y - S к Z - S в G - S. Множества Y, Z и S теперь предоставляют средства для расширения частичной декомпозиции.

Пусть множество S' состоит из всех узлов S, лежащих в Y U Z U C. Ситуация выглядит так, как показано на рис. 10.11. Заметим, что множество S' ∩ C не пусто: из каждого из множеств Y и Zвыходят ребра в C, и если бы множество S' ∩ C было пустым, то существовал бы путь от Y - S к Z - S в G - S, который начинается в Y, переходит прямо в C, проходит через C и, наконец, снова переходит в Z. Кроме того, |S'| ≤ |S| ≤ w.

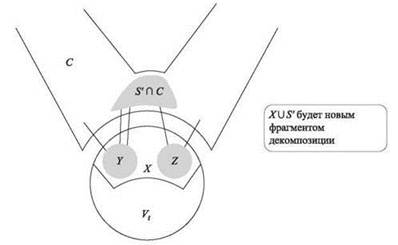
Рис. 10.11. Добавление нового фрагмента в частичную декомпозицию

Мы определяем новый фрагмент V = X U S', делая s листом t. Концы всех ребер из S' в U принадлежат X и |X U S'| ≤ 3w + w = 4w, так что частичная декомпозиция сохраняется. Более того, множество узлов, покрываемое нашей частичной декомпозицией, увеличилось, так как множество S' ∩ C не пусто. Следовательно, если нам удастся показать, что инвариант (*) по-прежнему выполняется, работа будет завершена. И здесь мы приходим к интуитивному представлению, которое мы пытались отразить при обсуждении рис. 10.10: при добавлении нового фрагмента X US' мы надеемся, что компонента C хорошо разделится на дальнейшие компоненты.

Конкретнее, наша частичная декомпозиция теперь покрывает U U S'; и там, где прежде была компонента C из G - U, сейчас могут быть несколько компонент C' ⊆ C из G - (U U S'). У каждой из этих компонент C' все ее соседи принадлежат X U S'; но мы должны дополнительно убедиться в том, что таких соседей не более 3w, чтобы не нарушался инвариант (*). Рассмотрим одну из таких компонент C'. Утверждается, что все ее соседи в X U S' принадлежат одному из двух подмножеств (X - Z) U S' или (X - Y) U S' и размер каждого из этих множество не превышает |X| ≤ 3w. Если бы это условие не выполнялось, то у C' был бы сосед, принадлежащий одновременно Y - S и Z - S, а следовательно, существовал бы путь через C' от Y - S к Z - S в G - S. Но, как было показано ранее, такого пути быть не может. Из этого следует, что (*) продолжает выполняться после добавления нового фрагмента, что завершает обоснование правильности работы алгоритма.

Наконец, что можно сказать о времени выполнения алгоритма? Во времени добавления нового фрагмента в частичную декомпозицию доминирует время, необходимое для проверки того, является ли множество X (w + 1)-связным, которое составляет O(f(w) ∙ m). Это происходит не более чем в n итерациях, так как в каждой итерации увеличивается количество задействованных узлов G. Следовательно, общее время выполнения равно O(f(w) ∙ mn).

Ниже перечислены основные свойства нашего алгоритма декомпозиции.

(10.21) Для заданного графа G и параметра w алгоритм древовидной декомпозиции, описанный в этом разделе, делает одно из двух:

♦ строит декомпозицию с шириной менее 4w, или

♦ сообщает (обоснованно), что граф G не имеет древовидной ширины менее w.

Время выполнения алгоритма равно O(f(w) ∙ mn), где функция f(∙) зависит только от w.