Алгоритмы - Разработка и применение - 2016 год
Задача о выборе центров - Аппроксимирующие алгоритмы
Задача о выборе центров, как и задача из предыдущего раздела, также относится к общей категории задач по распределению работы между серверами. Центральное место в ней занимает вопрос о том, где лучше разместить серверы; чтобы формулировка оставалась простой и понятной, мы не будем включать в задачу концепцию распределения нагрузки. Задача о выборе центров также дает пример случая, в котором наиболее естественный жадный алгоритм может привести к сколь угодно плохому решению, тогда как слегка измененный жадный метод гарантированно приводит к почти оптимальному решению.
Задача
Рассмотрим следующий сценарий: имеется множество S из n мест — допустим, n маленьких городков в сельской части штата Нью-Йорк. Требуется выбрать k мест для строительства больших торговых комплексов. Предполагается, что население каждого из n городков будет посещать один из торговых комплексов, поэтому места для строительства k торговых комплексов должны находиться в центральных точках.
Начнем с формального определения входных данных нашей задачи. Имеется целое число k, множество S из n мест (соответствующих городкам) и функция расстояния. Для экземпляров задачи, в которых местами являются точки на плоскости, функция расстояния будет стандартным евклидовым расстоянием между точками, а любая точка на плоскости может рассматриваться для размещения центра. Тем не менее разработанный нами алгоритм может применяться и для более общей концепции расстояния. На практике под расстоянием часто понимается расстояние по прямой, но также может пониматься время перемещения от точки s в точку z или расстояние вдоль дороги и даже расходы на перемещение. Допускается любая функция расстояния, обладающая следующими естественными свойствами:
♦ dist(s, s) = 0 для всех s ∈ S;
♦ симметричность: dist(s, z) = dist(z, s) для всех s, z ∈ S;
♦ неравенство треугольника: dist(s, z) + dist(z, h) ≥ dist(s, h).
Первое и третье свойства присущи практически всем естественным понятиям расстояния. И хотя существуют ситуации с асимметричными расстояниями, большинство случаев, представляющих интерес, также удовлетворяет второму свойству. Наш жадный алгоритм применяется к любой функции расстояния, обладающей этими тремя свойствами, и зависит от всех трех.
Затем необходимо прояснить, что же подразумевается под размещением “в центре”. Пусть C — множество центров. Предполагается, что жители каждого городка посещают ближайший торговый комплекс. Это подсказывает, что расстояния от места s до центров должны определяться в виде dist(s, C) = min c∈Cdist(s,c). Множество C образует r-покрытие, если каждое место находится на расстоянии не более r от одного из центров, то есть если dist(s, C) ≤ r для всех мест s ∈ S. Минимальное значение г, для которого C образует r-покрытие, называется радиусом покрытияC и обозначается r(C). Другими словами, радиус покрытия множества центров C определяется как максимальное расстояние, которое необходимо проехать, чтобы попасть к ближайшему центру. Нашей целью является выбор множества C из к центров, для которых величина r(C) минимальна.
Разработка и анализ алгоритма
Недостатки простого жадного алгоритма
Для начала обсудим жадные алгоритмы для этой задачи. Как и прежде, понятие “жадности” по необходимости получается несколько размытым; фактически мы рассматриваем алгоритмы, которые перебирают места одно за другим “недальновидно”, то есть при выборе каждого места не учитывается, куда попадут остальные.
Пожалуй, самый простой жадный алгоритм работает так: первый центр размещается в месте, лучше всего подходящем для одного центра, после чего центры добавляются для сокращения радиуса покрытия — каждый раз настолько, насколько это возможно. Как выясняется, такой подход излишне упрощен, чтобы быть эффективным: в некоторых случаях он приводит к очень плохим решениям.
Чтобы убедиться в этом, рассмотрим пример с двумя местами s и z и k = 2. Допустим, s и z располагаются на плоскости — на расстоянии, равном стандартному евклидовому расстоянию на плоскости, а любая точка плоскости подходит для размещения центра. Обозначим d расстояние между s и z. В этом случае лучшее расположение для одного центра c1 находится в середине пути между s и z, а радиус покрытия этого центра равен r({c1}) = d/2. Жадный алгоритм разместит первый центр в точке c1. Неважно, где бы ни был размещен второй центр, по крайней мере для одного из мест s и z центр c1 окажется ближе, поэтому радиус покрытия множества двух центров останется равным d/2. При этом в оптимальном решении с k = 2 центры размещаются в s и z, что приведет к радиусу покрытия 0. В более сложном примере, демонстрирующем ту же проблему, используются два плотных “скопления” мест возле s и z. Предложенный нами жадный алгоритм начнет с размещения центра в середине между скоплениями, тогда как в оптимальном решении создается отдельный центр для каждого скопления.
Знать оптимальный радиус полезно
Поиски улучшенного алгоритма мы начнем с полезного мысленного эксперимента. Представьте на минуту, что вам кто-то подсказал значение оптимального радиуса r. Пригодится ли эта информация? То есть предположим, что нам известно, что существует множество из k центров С* с радиусом r(С*) ≤ r и мы хотим найти некоторое множество из k центров из С, радиус покрытия которых ненамного больше r. Как выясняется, найти множество из k центров c радиусом покрытия, не превышающим 2r, относительно несложно.
Идея заключается в следующем: мы можем использовать факт существования этого решения С* в своем алгоритме несмотря на то, что мы не знаем, как выглядит С*. Рассмотрим любое место s∈ S. Должен существовать центр c* ∈ С*, покрывающий место s, и этот центр c* находится на расстоянии не более r от s. Теперь в качестве центра в нашем решении выбирается это место sвместо с*, потому что мы понятия не имеем, что собой представляет с*. Нам хотелось бы сделать так, чтобы из s покрывались все места, покрываемые с* в неизвестном решении С*. Задача решается увеличением радиуса с r до 2r. Все места, находившиеся на расстоянии не более r от центра с*, находятся на расстоянии не более 2r от s (это следует из неравенства треугольника). Простая иллюстрация этого аргумента представлена на рис. 11.4.

Рис. 11.4. Все места, покрываемые с радиусом r из с*, также покрываются с радиусом 2r из s

Очевидно, если этот алгоритм возвращает множество, содержащее не более к центров, мы получаем желаемый результат.
(11.6) У любого множества центров C, возвращаемого алгоритмом, радиус покрытия r(C) ≤ 2r.
Затем необходимо обосновать, что если алгоритм не возвращает множество центров, то его заключение об отсутствии множества с радиусом покрытия не более r действительно является верным:
(11.7) Предположим, алгоритм выбирает более к центров. Тогда для любого множества C* с размером не более к радиус покрытия r(C*) > r.
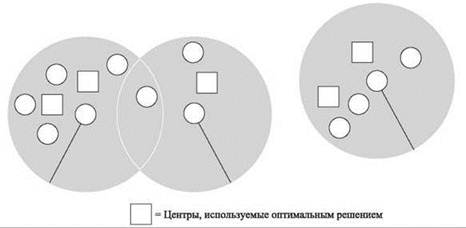
Рис. 11.5. Критический шаг в анализе жадного алгоритма, которому известен оптимальный радиус r. Никакой центр, используемый оптимальным решением, не может принадлежать двум разным кругам, поэтому количество оптимальных центров должно быть по крайней мере не меньше количества центров, выбранных жадным алгоритмом
Доказательство. Предположим обратное: существует множество C*, содержащее не более k центров, с радиусом покрытия r(C*) ≤ r. Каждый центр c ∈ C, выбираемый жадным алгоритмом, является одним из исходных мест в S, и множество С* имеет радиус покрытия не более r, поэтому должен быть центр с* ∈ С*, находящийся от с на расстоянии не более r, то есть dist(c, с*) ≤ r. Мы будем называть такой центр с* близким к с. Нам хотелось бы доказать, что ни один центр с* в оптимальном решении С* не может быть близким к двум разным центрам в жадном решении С. Если это удастся, работа закончена: у каждого центра с ∈ C имеется близкий оптимальный центр с* ∈ С*, и все эти близкие оптимальные центры различны. Из этого следует, что |С*| ≥ |C|, а поскольку |С| > k, это противоречит нашему предположению о том, что С* содержит не более k центров.
Итак, нужно лишь показать, что ни один оптимальный центр с* ∈ С не может быть близким к каждому из двух центров с, с' ∈ С. Причина изображена на рис. 11.5: каждая пара центров с, с' ∈ С разделяется расстоянием более 2r, поэтому нахождение с* на расстоянии не более r от каждого из них приведет к нарушению неравенства треугольника), поскольку dist(с, с*) + dist(c*, с') ≥ dist(с, с') > 2r. ■
Снятие предположения об известном оптимальном радиусе
Вернемся к исходному вопросу: как выбрать хорошее множество из k центров, если оптимальный радиус покрытия неизвестен?
Стоит рассмотреть два разных ответа на этот вопрос. Во-первых, при разработке аппроксимирующих алгоритмов часто бывает концептуально полезно предположить, что значение, обеспечиваемое оптимальным решением, известно. В таких ситуациях часто можно начать с алгоритма, спроектированного с учетом этого предположения, и преобразовать его в алгоритм, обеспечивающий сравнимые гарантии производительности простым перебором по диапазону “предположений” относительно оптимального значения. В ходе выполнения алгоритма эта последовательность предположений становится все более и более точной, пока не будет достигнуто приближенное решение.
Для задачи о выборе центров это может происходить так: мы начинаем с очень слабых исходных предположений относительно радиуса оптимального решения: известно, что оно больше 0 и что оно не превышает максимального расстояния rmax между любыми двумя местами. Итак, сначала мы делим разность между ними надвое и применяем разработанный выше жадный алгоритм со значением r = rmах/2. Затем в соответствии со структурой алгоритма происходит одно из двух: либо мы находим множество из к центров с радиусом покрытия не более 2r, либо заключаем, что решения с радиусом покрытия не более r не существует. В первом случае можно понизить оценку радиуса оптимального решения; во втором она должна быть повышена. Так по радиусу проводится своего рода “бинарный поиск”: алгоритм итеративно определяет значения r0 < r1, чтобы мы знали, что оптимальный радиус больше r0, но решение имеет радиус не более 2r1. По этим значениям описанный выше алгоритм выполняется с радиусом r = (r0 + r1)/2; затем мы либо решаем, что радиус оптимального решения больше r > r0, либо получаем решение с радиусом не более 2r = (r0 + r1) < 2r1. В любом случае оценка уточняется с одной или с другой стороны так же, как это происходит при бинарном поиске. Алгоритм прекращает работу, когда оценки r0 и r1 оказываются достаточно близкими друг к другу; в этой точке наше решение с радиусом 2r1 близко к 2-аппроксимации оптимального радиуса, так как мы знаем, что оптимальное решение больше r0 (а следовательно, близко к r1).
Работающий жадный алгоритм
В конкретном случае задачи о выборе центров существует неожиданный способ обойти предположение об известном радиусе, не прибегая к общему методу, описанному выше. Оказывается, жадный алгоритм в практически неизменном виде можно выполнить, ничего не зная о значении r.
Предыдущий жадный алгоритм, располагая информацией о r, многократно выбирает одно из исходных мест s как следующий центр; при этом он убеждается в том, что это место находится на расстоянии не менее 2r от всех ранее выбранных мест. Чтобы добиться практически того же эффекта, не зная г, можно просто выбрать место s, самое дальнее от всех ранее выбранных центров: если существуют места, находящиеся на расстоянии не менее 2r от всех ранее выбранных мест, то это самое дальнее место s должно быть одним из них. Ниже приведено описание алгоритма.

(11.8) Этот жадный алгоритм возвращает множество C из k точек — таких, что r(C) ≤ 2r(C*), где С* — оптимальное множество из k точек.
Доказательство. Обозначим r = r(С*) минимально возможный радиус множества из k центров. Предположим, что можно получить множество из k центров C с r(C) > 2r, и придем к противоречию.
Пусть s — место, находящееся на расстоянии более 2r от каждого центра в C. Рассмотрим промежуточную итерацию в ходе выполнения цикла, к моменту которой было выбрано множество центров C'. Предположим, в этой итерации добавляется центр с'. Утверждается, что с' находится на расстоянии не менее 2r от всех мест в C'. Это следует из того, что место s находится на расстоянии более 2r от всех мест в большем множестве C, а мы выбираем место с, самое дальнее от всех ранее выбранных центров. Формально имеется следующая цепочка неравенств:
![]()
Следовательно, наш жадный алгоритм правильно реализует первые k итераций цикла Пока предыдущего алгоритма, в котором был известен оптимальный радиус r: при каждой итерации добавляется центр, находящийся на расстоянии более 2r от всех ранее выбранных центров. Но у предыдущего алгоритма после выбора k центров S' ≠ ø, так как s ∈ S', поэтому он продолжит работу, выберет более k центров и в конечном итоге придет к заключению, что k центров не могут иметь радиус покрытия не более r. Это противоречит нашему выбору r, и такое противоречие доказывает, что r(С) ≤ 2r. ■
Обратите внимание на удивительный факт: наш итоговый жадный 2-аппроксимирующий алгоритм представляет собой очень простую модификацию первого (неработающего) жадного алгоритма. Вероятно, самое важное изменение заключается в том, что наш алгоритм всегда выбирает в качестве центров готовые места (то есть торговый комплекс будет построен в одном из городков, а не на середине пути между ними).