Линейное программирование и округление: применение к задаче о вершинном покрытии - Аппроксимирующие алгоритмы

Для начала познакомимся с эффективным методом из области исследования операций: линейным программированием. Дисциплина линейного программирования становится темой целых учебных курсов, и мы даже не пытаемся привести здесь сколько-нибудь исчерпывающий обзор. В этом разделе будут представлены некоторые базовые идеи, лежащие в основе линейного программирования, а также продемонстрированы возможности их применения для аппроксимации NР-сложных оптимизационных задач.

Напомним, что в разделе 11.4 мы разработали 2-аппроксимирующий алгоритм для взвешенной задачи о вершинном покрытии. В первом примере использования метода линейного программирования мы рассмотрим другой 2-аппроксимирующий алгоритм, который концептуально намного проще первого (хотя и работает медленнее).

Линейное программирование как обобщенный метод

Наш 2-аппроксимирующий алгоритм взвешенной версии задачи о вершинном покрытии будет основан на линейном программировании. Линейное программирование описывается здесь не для того, чтобы дать общий алгоритм аппроксимации, а чтобы продемонстрировать его мощь и универсальность.

Что же такое линейное программирование? Чтобы ответить на этот вопрос, будет полезно для начала вспомнить из линейной алгебры задачу системы линейных уравнений. B матрично-векторной записи имеется вектор x неизвестных вещественных чисел, заданная матрица A и заданный вектор b; требуется решить уравнение Ax = b. Многим хорошо известен метод исключения Гаусса, позволяющий эффективно решать такие задачи.

Базовая задача линейного программирования может рассматриваться как более сложная версия этой задачи, в которой равенства заменены неравенствами. Говоря конкретнее, рассмотрим задачу определения вектора x, удовлетворяющего неравенству Ax ≥ b. Под этой записью мы имеем в виду, что каждая координата вектора Ax должна быть больше либо равна соответствующей координаты вектора b. Такие системы неравенств определяют области в пространстве. Например, предположим, x = (x₁, x₂) — двумерный вектор, и имеются четыре неравенства:

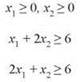
В этом случае множество решений определяет область на плоскости, изображенную на рис. 11.10. Для заданной области, определяемой уравнением Ax ≥ b, линейное программирование стремится минимизировать линейную комбинацию координат x по всем x, принадлежащим области.

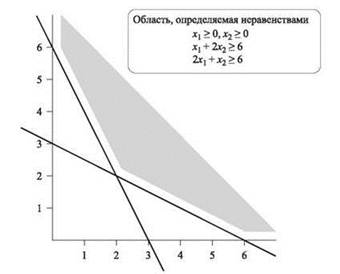
Рис. 11.10. Область допустимых решений простой задачи линейного программирования

Такая линейная комбинация может быть записана в виде c^tx, где c — вектор коэффициентов, а c^tx обозначает скалярное произведение двух векторов. Таким образом, стандартная форма линейного программирования как задачи оптимизации выглядит следующим образом.

Для заданной матрицы A с размерами m х n, векторов b ∈ R^m и c ∈ Rⁿ найти вектор x ∈ Rⁿ для решения следующей задачи оптимизации:

min(c^tx для x ≥ 0; Ax ≥ b).

c^tx часто называется целевой функцией линейной программы, а Ax ≥ b называется набором ограничений. Например, в примере на рис. 11.10, допустим, определяется вектор c (1,5, 1); другими словами, мы стремимся минимизировать величину 1,5x₁ + x₂ по области, определяемой неравенствами.

Задача решается выбором точки x = (2,2), в которой пересекаются две наклонные линии; в ней c^tx = 5, и вы можете убедиться, что получить меньшее значение невозможно.

Задачу линейного программирования можно сформулировать как задачу принятия решения следующим образом:

Для заданной матрицы A, векторов b и c, и границы у существует ли такое значение x, для которого x ≥ 0, Ax ≥ b, и c^tx ≤ γ?

Чтобы избежать проблем, связанных с представлением вещественных чисел, мы будем считать, что координаты в векторах и матрице являются целыми числами.

Вычислительная сложность линейного программирования

Версия задачи линейного программирования с принятием решения принадлежит NP. Интуитивно это вполне понятно — нужно лишь представить вектор x, обладающий нужными свойствами. Единственная проблема в том, что даже если все входные числа являются целыми, координаты такого вектора x могут быть нецелыми, и для их представления может потребоваться очень большая точность: откуда известно, что мы сможем читать и обрабатывать эти данные за полиномиальное время? Но на самом деле можно показать, что если решение существует, то существует и рациональное решение, для записи которого достаточно полиномиального количества битов, так что это не проблема.

Кроме того, уже давно известно, что задачи линейного программирования относятся к классу co-NP, хотя это и не очевидно. Студенты, прошедшие курс линейного программирования, могут заметить, что этот факт следует из двойственности линейного программирования².

В течение долгого времени линейное программирование, пожалуй, было самым известным примером задачи, принадлежащей NP и co-NP, для которой не известно решение с полиномиальным временем. Затем в 1981 году Леонид Хачиян, который в то время был молодым ученым из СССР, предложил алгоритм с полиномиальным временем для этой задачи. Американская массовая пресса забеспокоилась, не сыграет ли это открытие ту же роль, что и запуск спутника в период холодной войны, но этого не произошло, и вскоре ученые разобрались в том, что же сделал Хачиян. Его исходный алгоритм работал с полиномиальным временем, но был довольно медленным и непригодным для практического применения; но с тех пор после выхода работы Нарендры Кармаркара в 1984 году были разработаны практичные алгоритмы с полиномиальным временем — так называемые методы внутренней точки.

Пример линейного программирования также интересен и по другой причине. Самым распространенным алгоритмом для решения этой задачи является симплексный метод. Он очень хорошо работает на практике и в реальных задачах может успешно конкурировать с внутренними методами, работающими с полиномиальным временем. Тем не менее известно, что в худшем случае он выполняется за полиномиальное время; просто экспоненциальное поведение очень редко встречается на практике. По этой причине линейное программирование стало очень полезным и важным примером для анализа ограничений полиномиального времени как формального определения эффективности.

Впрочем, для наших целей важно то, что задачи линейного программирования могут решаться за полиномиальное время, и на практике существуют очень эффективные алгоритмы. На курсах линейного программирования вы сможете получить гораздо больше информации по этой теме, а нас сейчас интересует следующий вопрос: как линейное программирование помогает при решении таких комбинаторных задач, как задача о вершинном покрытии?

Задача о вершинном покрытии как целочисленная программа

Вспомните, что вершинным покрытием в графе G = (V, E) называется такое множество S ⊆ V, что у каждого ребра в графе хотя бы один конец принадлежит S. Во взвешенной задаче о вершинном покрытии каждая вершина i ∈ V имеет вес w_i ≥ 0, а вес множества S обозначается Требуется найти вершинное покрытие S, для которого значение w(S) минимально.

Попробуем сформулировать линейную программу, которая находится в близком соответствии с задачей о вершинном покрытии. Следовательно, мы рассматриваем граф G = (VE) с весом w_i ≥ 0 для каждого узла i. Линейное программирование основано на использовании векторов переменных. В нашем случае с каждым узлом i ∈ V связывается переменная х, которая моделирует выбор о том, нужно ли включать узел i в вершинное покрытие; х_i = 0 означает, что узел i не входит в вершинное покрытие, а с х_i = 1 узел включается в него. Мы создадим один n-мерный вектор х, в котором i-я координата соответствует i-й переменной решения х_i.

Требование о том, что выбранные узлы образуют вершинное покрытие, будет закодировано с использованием линейных неравенств, а цель минимизации общего веса кодируется при помощи целевой функции. У каждого ребра (i, j) ∈ E один конец должен находиться в вершинном покрытии, и мы запишем этот факт в виде неравенства х_i + х_j ≥ 1. Наконец, для выражения задачи минимизации множество весов записывается в виде n-мерного вектора w, в котором i-я координата соответствует w_i; мы стремимся минимизировать w^tx.

В итоге задача о вершинном покрытии формулируется следующим образом.

Утверждается, что вершинные покрытия G однозначно соответствуют решениям х этой системы линейных неравенств, в которой все координаты равны 0 или 1.

(11.21) S является вершинным покрытием G в том, и только в том случае, если вектор х, в котором x_i = 1 для i ∈ S, и x_i = 0 для i ∉ S, удовлетворяет ограничениям в (VC.IP). Кроме того, w(S) = w^tx.

Эта система может быть переведена в матричную форму, используемую для линейного программирования. Мы определяем матрицу А, столбцы которой соответствуют узлам в V, а строки — ребрам в E; элемент А[е, i] = 1, если узел i является концом ребра е, и 0 в противном случае. (Каждая строка содержит ровно два ненулевых элемента.) Если использовать 1 для обозначения вектора, все координаты которого равны 1, а 0 — для обозначения вектора, все координаты которого равны 0, то система неравенств может быть записана в следующем виде:

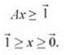
Однако следует помнить, что это не просто экземпляр задачи линейного программирования: мы выдвинули критичное требование о том, что все координаты в решении равны 0 или 1. Итак, из нашей формулировки следует, что нужно решить задачу min(w^tx subject to имеет целые координаты.)

В этом экземпляре задачи о линейном программировании координаты х принимают целые значения; без дополнительного ограничения координаты х могут быть произвольными вещественными числами. Назовем ее задачей целочисленного программирования, так как мы ищем целочисленные решения для задачи линейного программирования.

Целочисленное программирование существенно сложнее линейного; однако в нашем обсуждении в действительности происходит сведение задачи о вершинном покрытии к версии задачи целочисленного программирования с принятием решения, иначе говоря, мы доказали, что

(11.22) Вершинное покрытие ≤_р Целочисленное программирование

Чтобы продемонстрировать NP-полноту целочисленного программирования, необходимо еще установить, что версия с принятием решения принадлежит NP. И здесь возникают сложности, как и в случае с линейным программированием, поскольку мы должны доказать, что всегда существует решение х, которое может быть записано с полиномиальным количеством битов. Тем не менее это возможно доказать. В нашем случае задача целочисленного программирования явно ограничивается решениями, в которых каждая координата равна либо 0, либо 1; очевидно, такая задача принадлежит NP, а сведение от вершинного покрытия устанавливает, что даже этот особый случай является NP-полным.

Использование линейного программирования для задачи вершинного покрытия

Пока еще не совсем понятно, принесет ли реальную пользу наш экскурс в линейное и целочисленное программирование или же мы окажемся в тупике. Очевидно, попытки оптимального решения задачи целочисленного программирования (VC.IP) бесперспективны, так как эта задача является NP-сложной.

Чтобы добиться результатов, мы воспользуемся тем фактом, что линейное программирование обладает меньшей сложностью, чем целочисленное программирование. Допустим, мы возьмем задачу (VC.IP) и изменим ее, сняв требование х_i ∈ {0,1}, и вернемся к ограничению, в соответствии с которым х_i является произвольным вещественным числом от 0 до 1. При этом будет получен экземпляр задачи линейного программирования (назовем его (VC.LP)), который решается за полиномиальное время: мы можем найти множество значений {х*_i} в диапазоне от 0 до 1, такие что х*_i + х*_j ≥ 1 для каждого ребра (i, j) и значение ∑_iw_ix*_i минимизировано. Обозначим этот вектор х*, а значение целевой функции w_LP = w^tх*.

Выделим следующий базовый факт:

(11.23) Пусть S* — вершинное покрытие с минимальным весом. Тогда w_LP ≤ w(S*).

Доказательство. Вершинные покрытия G соответствуют целочисленным решениям (VC.IP), так что минимум по всем целочисленным векторам х точно совпадает с вершинным покрытием минимального веса. Чтобы получить минимум для линейной программы (VC.LP), мы разрешим х принимать произвольные вещественные значения, то есть минимизация производится по много большему количеству вариантов х, а следовательно, минимум (VC.LP) не больше минимума (VC.IP). ■

Утверждение (11.23) — один из ключевых ингредиентов, необходимых для алгоритма аппроксимации: хорошая нижняя граница для оптимума в форме эффективно вычисляемой величины w_LP.

Однако w_LP определенно может быть меньше w(S*). Например, если граф G представляет собой треугольник, а все веса равны 1, то минимальное вершинное покрытие имеет вес 2. Но в решении задачи линейного программирования мы можем присвоить х_i = 1/2 всем трем вершинам и получить решение с весом только 3/2. Если нужен более общий пример, возьмем граф с nузлами, в котором каждая пара узлов соединяется ребром. Все веса снова равны 1. Минимальное вершинное покрытие имеет вес n - 1, но мы можем найти решение линейного программирования со значением n/2, присвоив х_i = 1/2 для всех вершин i.

Возникает вопрос: как решение этой задачи линейного программирования поможет найти вершинное покрытие, близкое к оптимальному? Идея заключается в том, чтобы работать со значениями х*_i и по ним вычислить вершинное покрытие S. Вполне естественно, что если х*_i = 1 для некоторого узла i, то этот узел включается в вершинное покрытие S, а если х*_i = 0, то узел остается за пределами S. Но что делать с дробными промежуточными значениями? Что делать, если х*_i = 0,4 или х*_i = 0,5? В таких ситуациях естественно воспользоваться округлением.

Для заданного дробного решения {х*} мы определяем S = I ∈ V: х*_i ≥ 1/2}, то есть значения от 1/2 округляются в большую сторону, а значения, меньшие 1/2, округляются в меньшую сторону.

(11.24) Множество S, определяемое таким образом, является вершинным покрытием, и w(S) ≤ w_LP.

Доказательство. Сначала докажем, что S является вершинным покрытием. Рассмотрим ребро e = (i, j). Утверждается, что по крайней мере одна из вершин i и j должна входить в S. Вспомните, что одно из неравенств х_i + х_j ≥ 1. Следовательно, в любом решении х*, удовлетворяющем этому неравенству, либо х*_i > 1/2, либо х*_j > 1/2. По крайней мере одна из этих величин будет округлена в большую сторону, и i или j включается в S.

Теперь рассмотрим вес w(S) этого вершинного покрытия. Множество S включает вершины только с х*_i ≥ 1/2; следовательно, экземпляр линейного программирования “заплатил” по крайней мере 1/2w_i за узел i, а мы платим w_i; — максимум вдвое больше. В более формальном виде используется следующая цепочка неравенств:

Таким образом, мы создали вершинное покрытие S с весом не более 2w_LP. Нижняя граница в (11.23) показывает, что оптимальное вершинное покрытие имеет вес не менее w_LP, поэтому имеем следующий результат:

(11.25) Алгоритм строит вершинное покрытие S, вес которого не более чем вдвое превышает минимально возможный.