Задача оптимизации в перспективе - Локальный поиск

В двух предыдущих главах рассматривались методы работы с вычислительно-неразрешимыми задачами: в главе 10 — выявление структурированных особых случаев NР-сложных задач, а в главе 11 — разработка аппроксимирующих алгоритмов с полиномиальным временем. В этой главе рассматривается третья и последняя тема, относящаяся к этой области: разработка алгоритмов локального поиска.

Локальный поиск — чрезвычайно универсальный прием; этим термином описываются любые алгоритмы, которые последовательно “исследуют” пространство возможных решений, перемещаясь за один шаг от текущего решения к другому, “ближнему”. Общность и гибкость этого метода имеют свои преимущества: алгоритм на базе локального поиска можно без особых трудностей разработать почти для любой вычислительно сложной задачи; с другой стороны, часто бывает очень трудно сказать что-нибудь конкретное или доказуемое о качестве решений, находимых алгоритмом локального поиска, и, соответственно, очень сложно определить, хороший или плохой алгоритм локального поиска используется в каждом конкретном случае.

Эти достоинства и недостатки будут отражены в ходе рассмотрения локального поиска в этой главе. Алгоритмы локального поиска обычно представляют собой эвристики, предназначенные для нахождения хороших (но не обязательно оптимальных) решений вычислительных задач, и для начала мы поговорим о том, как выглядит поиск таких решений на глобальном уровне. Полезная интуитивно понятная аналогия существует в принципе минимизации энергии в физике, поэтому мы сначала исследуем этот вопрос. Стиль изложения в этой главе несколько отличается от того, что был в книге до настоящего момента; мы представим некоторые алгоритмы, обсудим их на качественном уровне, но честно признаем, что мало что из этого мы можем доказать.

Впрочем, в отдельных случаях нам удастся доказать некоторые свойства алгоритмов локального поиска и связать их производительность с оптимальным решением. Эта тема займет центральное место в завершающей части этой главы: мы начнем с рассмотрения случая (динамики нейронных сетей Хопфилда), в котором локальный поиск предоставляет естественную точку зрения на поведение сложного процесса; затем мы сосредоточим внимание на NР-сложных задачах, для которых локальный поиск помогает разработать эффективные алгоритмы с доказуемыми гарантиями аппроксимации. Глава завершается обсуждением других типов локального поиска: динамикой наилучших ответов и равновесиями Нэша, естественным образом встречающимися при изучении систем с множеством взаимодействующих агентов.

12.1. Задача оптимизации в перспективе

Основные концепции локального поиска были разработаны учеными, мыслившими аналогиями с физикой. Рассматривая широкий спектр сложных вычислительных задач, требующих минимизации некоторой величины, они рассуждали следующим образом: физические системы постоянно решают задачу минимизации, стремясь к минимуму потенциальной энергии. Чему можно научиться, наблюдая за минимизацией в природе? Не подскажет ли она какие-нибудь новые алгоритмы?

Потенциальная энергия

Если бы мир выглядел так, как нам рассказывают в начальном курсе механики, он состоял бы исключительно из хоккейных шайб, скользящих по льду, и шаров, скатывающихся по наклонным поверхностям. Шайба скользит, потому что ее толкнули; но почему шары скатываются вниз? Из ньютоновской механики известно, что шар стремится минимизировать свою потенциальную энергию. В частности, если шар имеет массу m и падает на расстояние h, он теряет потенциальную энергию, пропорциональную mh. Итак, если отпустить шар у верхнего края воронкообразного углубления (рис. 12.1), его потенциальная энергия будет минимальной в самой нижней точке.

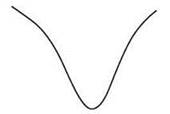
Рис. 12.1. Когда поверхность потенциальной энергии имеет структуру простой воронки, найти нижнюю точку достаточно легко

При усложнении структуры поверхности проявляются дополнительные сложности. Возьмем “двойную воронку” на рис. 12.2. Точка A находится ниже точки B, поэтому она является предпочтительной для нахождения шара в состоянии покоя. Но если шар скатывается с точки C, он не сможет преодолеть барьер между двумя воронками и окажется в B. В таких случаях говорят, что шар попал в локальный минимум: он находится в самой нижней точке, если рассматривать окрестности текущего положения; но если отступить и взглянуть на ситуацию в целом, мы видим, что глобальный минимум не достигнут.

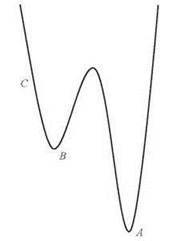
Рис. 12.2. Большинство поверхностей сложнее простых воронок; например, в этой “двойной воронке” существуют большой глобальный минимум и меньший локальный минимум

Конечно, очень большие физические системы также должны стремиться к минимизации своей энергии. Представьте, например, что вы взяли несколько граммов однородного вещества, нагрели его и изучаете его поведение во времени. Чтобы точно отразить потенциальную энергию образца, теоретически необходимо представить поведение каждого атома вещества и его взаимодействие с ближними атомами. Но также будет полезно рассмотреть свойства системы в целом (то есть всего образца), и здесь на помощь приходит статистическая механика. Мы еще вернемся к статистической механике, а пока просто заметим, что концепция “поверхности потенциальной энергии” предоставляет полезную и наглядную аналогию для процесса, который используется в больших физических системах для минимизации энергии. Следовательно, хотя в действительности для представления настоящей поверхности потенциальной энергии потребовалось бы многомерное пространство с огромным количеством измерений, мы можем воспользоваться одномерным условным представлением для обсуждения различий между локальными и глобальными энергетическими минимумами, окружающих их “потенциальных ям” и “высоты” энергетических барьеров между ними.

Остывание расплавленного материала с попыткой формирования идеального кристаллического тела в действительности представляет собой процесс перехода совокупности атомов в состояние глобального минимума потенциальной энергии. Этот процесс может быть очень сложным, и большое количество локальных минимумов в типичной поверхности потенциальной энергии представляет многочисленные отклонения, которые могут привести к сбоям при поиске глобального минимума системой. Следовательно, вместо простого примера на рис. 12.2, который содержит всего один неправильный вариант, нам следует беспокоиться о поверхностях, схематически изображенных на рис. 12.3. Это своего рода “гребенка”, в которой локальные минимумы подстерегают систему на всем пути от верха до низа.

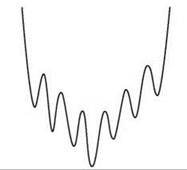
Рис. 12.3. Обобщенная поверхность потенциальной энергии может содержать множество локальных минимумов, усложняющих поиск глобального минимума, как в изображенной на рисунке “гребенке”

Связь с оптимизацией

Этот подход к минимизации энергии в действительности базируется на нескольких основных положениях: физическая система может находиться в одном из многочисленных состояний; ее энергия является функцией текущего состояния; небольшое возмущение в заданном состоянии приводит к “соседнему” состоянию. Структура связи этих соседних состояний вместе со структурой энергетической функции определяет энергетическую поверхность.

Под этим углом мы снова взглянем на задачу вычислительной минимизации. В типичной задаче такого рода имеется большое (как правило, имеющее экспоненциальный размер) множество Cвозможных решений. Также понадобится функция стоимостиc(∙), оценивающая качество каждого решения; для решения S ∈ C его стоимость записывается в виде c(S). Целью является поиск решения S* ∈ C с наименьшим возможным значением (S*).

До настоящего момента мы рассматривали подобные задачи именно так. А теперь добавим в решения понятие соседских отношений, отражающих идею о том, что одно решение S' может быть получено незначительным изменением другого решения S. Запись S ~ S' означает, что S' является соседним решениемS, а множество соседей S, то есть {S': S ~ S'}, будет обозначаться N(S). Нас в первую очередь интересуют симметричные соседские отношения, хотя основные рассматриваемые принципы также распространяются и на асимметричные соседские отношения. Здесь принципиально то, что хотя множество C возможных решений и функция стоимости c(∙) предоставляются в спецификации задачи, мы свободны выбирать соседские отношения по своему усмотрению.

Алгоритм локального поиска получает эту конфигурацию, включая соседские отношения, и работает по следующей высокоуровневой схеме. Он постоянно поддерживает текущее решение S ∈ C. На каждом шаге он выбирает соседа S' решения S, объявляет S' новым текущим решением и повторяет процесс. На протяжении всего выполнения алгоритма запоминается решение с наименьшей стоимостью из всех встречавшихся; итак, по мере выполнения постепенно находятся все лучшие и лучшие решения. Суть алгоритма локального поиска заключается в выборе соседских отношений и в формулировке правила выбора соседнего решения на каждом шаге.

Итак, соседские отношения можно рассматривать как определяющий (обычно ненаправленный) граф множества всех возможных решений, в котором ребра соединяют соседние пары решений. В этом случае алгоритм локального поиска может рассматриваться как обход графа с попыткой перемещения в направлении хорошего решения.

Локальный поиск в задаче о вершинном покрытии

Без конкретной задачи все эти рассуждения выглядят довольно туманно; рассмотрим работу локального поиска на примере задачи о вершинном покрытии. Учтите, что задача о вершинном покрытии является хорошим примером, но существует много других задач оптимизации, которые с таким же успехом можно использовать в качестве примера.

Итак, имеется граф G = (V, E); множество C возможных решений состоит из всех подмножеств S множества V, образующих вершинные покрытия. Например, всегда выполняется V ∈ C. Стоимость c(S) вершинного покрытия Sравна его размеру; таким образом, минимизация стоимости вершинного покрытия эквивалентна нахождению покрытия с минимальным размером. Наконец, в наших примерах алгоритмов локального поиска будет использоваться очень простое соседское отношение: мы говорим, что S ~ S', если решение S' может быть получено из Sдобавлением или удалением одного узла. Таким образом, наши алгоритмы локального поиска будут обходить пространство возможных вершинных покрытий, добавляя или удаляя из текущего решения узел на каждом шаге и пытаясь найти как можно меньшее вершинное покрытие.

У этого соседского отношения есть одно полезное свойство:

(12.1) Каждое вершинное покрытие S имеет не более n соседних решений.

Утверждение доказывается попросту тем, что каждое соседнее решение S получается добавлением или удалением узла. Из (12.1) следует, что в процессе выбора можно эффективно исследовать все возможные соседние решения S.

Для начала рассмотрим очень простой алгоритм локального поиска — метод градиентного спуска. Градиентный спуск начинает с полного вершинного покрытия V и использует следующее правило выбора соседнего решения.

Обозначим S текущее решение. Если существует соседнее решение S' со строго меньшей стоимостью, то выбрать соседа, имеющего как можно меньшую стоимость. В противном случае завершить работу алгоритма.

Итак, метод градиентного спуска двигается строго вниз, пока может; когда дальнейшее движение становится невозможным, он останавливается.

Мы видим, что градиентный спуск завершается точно в тех решениях, которые являются локальными минимумами: то есть в таких решениях S, что для всех соседних S' выполняется c(S) ≤c(S').

Это определение очень точно соответствует нашему понятию локального минимума на энергетических поверхностях: это те точки, для которых одношаговое возмущение не улучшает функции стоимости.

Как наглядно представить поведение алгоритма локального поиска в контексте энергетических поверхностей, которые были представлены ранее? Начнем с градиентного спуска. Конечно, простейший экземпляр вершинного покрытия представляется n-узловым графом без ребер. Пустое множество является оптимальным решением (ребер для покрытия нет), а градиентный спуск превосходно справляется с нахождением этого решения: он начинает с полного множества вершин V и продолжает удалять узлы, пока не останется ни одного. В самом деле, множество вершинных покрытий для этого графа без ребер естественно соответствует воронке на рис. 12.1: единственный локальный минимум также является глобальным минимумом, и к нему существует нисходящий путь от любой точки.

Когда метод градиентного спуска работает неправильно? Рассмотрим “граф-звезду” G, состоящий из узлов x₁, y₁, y₂, ..., y_n-1, в котором узел x₁ соединен с каждым из узлов у_i. Минимальное вершинное покрытие для G представляет собой одноэлементное множество {x₁}, а градиентный спуск может достигнуть этого решения, последовательно удаляя у₁, ..., y_n-1 в любом порядке. Но если градиентный спуск начнет с удаления x₁, он немедленно оказывается в тупике: ни один узел y_i не может быть удален без разрушения свойства вершинного покрытия, поэтому единственным соседним решением является полное множество узлов V, обладающее более высокой стоимостью. Алгоритм “застревает” в локальном минимуме {y₁, y₂, ..., y_n-1}, обладающем очень высокой стоимостью по сравнению с глобальным минимумом.

В графическом виде мы оказываемся в ситуации, соответствующей “двойной воронке” на рис. 12.2. Глубокая воронка соответствует оптимальному решению {x₁}, а мелкая воронка соответствует локальному минимуму {y₁, y₂, ..., y_n-1}. Спуск по неправильно выбранному склону, выбранному в самом начале, может привести к неправильному минимуму. Ситуация легко обобщается до двух минимумов с любыми относительными глубинами. Допустим, имеется двудольный граф G с узлами x₁, x₂, ..., x_k и y₁, y₂, ..., y_l, where k < l и существует ребро из каждого узла вида x_i в узел вида y_j. Тогда существуют два локальных минимума, соответствующих вершинным покрытиям {x₁, ..., x_k} и {y₁, ..., y_l}. Какой из этих минимумов будет обнаружен при выполнении градиентного спуска, зависит исключительно от того, будет ли первым удален элемент вида x_i или y_i.

Для более сложных графов часто бывает полезно подумать о том, какую поверхность они представляют; и наоборот, иногда можно взглянуть на поверхность и подумать о том, какой граф мог бы ее породить.

Например, какой граф мог бы породить экземпляр задачи о вершинном покрытии с поверхностью вроде “гребенки” на рис. 12.3? Одним из таких графов мог бы быть n-узловой путь, в котором n — нечетное число, а узлы помечены в порядке v₁, v₂, ..., v_n. Уникальное минимальное вершинное покрытие S* состоит из всех узлов v_i, для которых i четно. Наряду с ним существует множество локальных оптимумов. Например, рассмотрим вершинное покрытие {v₂, v₃, v₅, v₆, v₈, v₉, ...}, в котором опущен каждый третий узел. Это вершинное покрытие существенно больше S*; при этом из него невозможно удалить ни один узел, сохранив покрытие всех ребер. Как выясняется, найти минимальное вершинное покрытие S* методом градиентного спуска, начиная с полного вершинного покрытия V, очень трудно: после удаления одного узла v_i с четным значением i возможность нахождения глобального оптимума S* полностью теряется. Таким образом, различие между четными и нечетными узлами создает множество ошибочных путей для локального поиска, что и придает общей поверхности вид “гребенки”. Конечно, между впадинами на рисунке и локальными оптимумами не существует прямого соответствия; как мы предупреждали ранее, рис. 12.3 всего лишь дает наглядное представление о происходящем.

Но мы видим, что даже для графов с очень простой структурой градиентный спуск слишком прямолинеен для алгоритма локального поиска. Обратимся к более эффективным алгоритмам локального поиска, которые используют аналогичные соседские отношения, но включают возможность “выхода” из локального минимума.