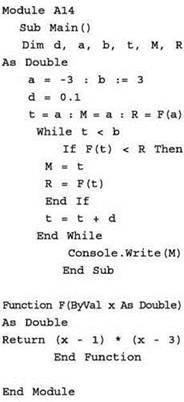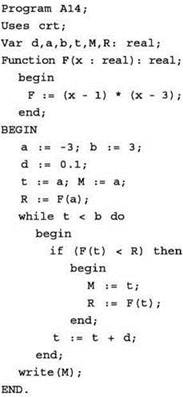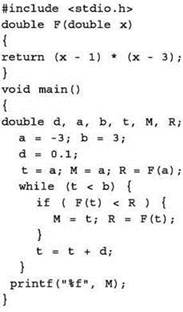Процедуры и функции - Программирование

Конспект

Подпрограмма

Подпрограмма — это поименованная или каким-либо иным образом обозначенная часть программы, которая может быть многократно вызвана из разных частей основной программы для выполнения неких “типовых” вычислений, в том числе для различных исходных данных.

Идея здесь состоит в следующем. Предположим, что некоторая часть алгоритма по своей сути повторяется в программе несколько раз. Так, в комбинаторике при вычислении количества сочетаний из п элементов по k (подмножеств из k элементов, взятых произвольно из множества n элементов и различающихся хотя бы одним элементом без учёта порядка их следования) используется формула:

В ней трижды надо вычислять факториал для трёх разных исходных значений. Тогда вычисление факториала путём выполняемых в цикле умножений можно оформить в виде подпрограммы, а затем обращаться к ней, каждый раз передавая этой подпрограмме требуемое исходное значение.

Иногда в виде подпрограмм выделяют фрагменты программного кода, выполняющие какие-либо типовые действия, — например, реализующие какие-то элементы интерфейса с пользователем. Это позволяет создавать отдельные библиотеки подпрограмм, облегчая этим работу программисту: ему уже не нужно отвлекаться на реализацию подобных “мелочей” и можно сосредоточиться непосредственно на сути решаемой вычислительной задачи, а библиотека готовых подпрограмм просто подключается к созданному листингу перед его компиляцией (или во время неё). А в современных ОС (например, в Windows) такие подпрограммы, уже откомпилированные в файлы DLL, являются основой функционирования как самой ОС, так и работающих в её среде прикладных программ и обеспечивают унификацию компонентов интерфейса.

Наконец, деление исходного сложного алгоритма на подпрограммы позволяет обеспечить его структуризацию, облегчить понимание и разработку программного продукта, разделить исходную задачу на более простые подзадачи, реализуя тем самым принцип нисходящего программирования (“от общего к частному”).

Функция

Это одна из двух возможных разновидностей подпрограмм. Её отличительная особенность состоит в том, что функция, принимая на вход любое количество исходных данных (аргументов), может возвращать только одно значение, которое передается как значение самой этой функции.

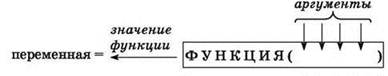
Для работы с подпрограммами-функциями в языке Паскаль (и аналогично — в большинстве других современных процедурных языков высокого уровня) требуется знание следующих особенностей.

1. Подпрограмма-функция должна быть описана в начале программы — после объявления используемых в ней глобальных констант, меток и переменных, но до собственно текста основной программы, заключенного в операторные скобки BEGIN и END (для наглядности эти слова, обрамляющие текст основной программы, записаны прописными буквами).

2. Описание подпрограммы-функции начинается со строки

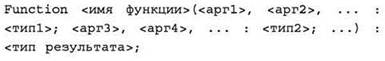
Здесь:

• Function — зарезервированное слово, указывающее транслятору, что далее идёт описание подпрограммы-функции;

• <имя функции> — идентификатор, выбираемый по тем же правилам, что и для имён переменных;

• сразу после имени функции в скобках записывается перечень передаваемых в эту функцию формальных параметров — имён переменных, которые далее будут использоваться при вычислениях, выполняемых в этой функции. При этом формальные параметры группируются через запятую в блоки одинаковых типов, а обозначения их типов записываются после списка параметров через двоеточие, как принято в Паскале при определении переменных; блоки параметров различного типа записываются через точку с запятой;

• после закрывающей скобки, также через двоеточие, записывается тип результата, который будет возвращать функция.

Пример:

Function F (х : real) : real; —объявляется подпрограмма-функция с именем F, которая принимает на вход одно действительное (тип real) число х и возвращает также действительное (real, записанное после скобок) значение результата.

3. После строки определения функции записывается её программный код. Правила его записи аналогичны правилам записи основной программы:

• сначала может присутствовать раздел описания локальных констант и переменных; эти константы и переменные действуют только в пределах данной функции и могут иметь такие же имена, что и локальные переменные, объявленные в других подпрограммах (транслятор их не путает);

• далее между операторными скобками begin и end записывается текст подпрограммы.

4. В конце текста подпрограммы значение, которое функция должна возвращать в качестве результата, нужно обязательно присвоить специальной переменной, имя которой совпадает с именем самой функции (причём отдельно объявлять эту переменную не нужно).

5. В тексте основной программы вызов функции производится следующим образом:

• записывается имя функции, а после него в скобках через запятую — список фактических параметров — константы, имена переменных, выражения, а также другие вызовы функций, значения которых нужно передать в функцию для выполнения вычислений. При этом количество и типы таких фактических параметров должны соответствовать указанным в объявлении функции формальным параметрам. Каждый фактический параметр при вызове функции записывается в соответствующий ему по порядку следования в списке формальный параметр и тем самым попадает в выполняемые функцией вычисления. При этом если для формального параметра указан соответствующий составной тип, объявленный в разделе type основной программы, то в подпрограмму может быть передан, например, массив целиком;

• поскольку функция возвращает значение, её запись (вместе с фактическими параметрами в скобках) должна быть либо включена в состав выражения, либо записана после имени переменной и следующего за ней оператора присваивания, либо указана как параметр в процедуре вывода на экран, записи в файл и пр. Иначе возвращённое функцией значение будет потеряно.

Процедура

Отличительная особенность подпрограммы-процедуры (или просто — процедуры) состоит в том, что она (в отличие от функции) может как принимать на вход, так и возвращать любое количество данных, причём все они записываются в качестве аргументов процедуры.

Для работы с процедурами в языке Паскаль (и в большинстве других языков высокого уровня) требуется знать следующее.

1. Процедура должна быть описана в начале программы — после объявления используемых в ней глобальных констант, меток и переменных, но до собственно текста основной программы, заключённого в операторные скобки BEGIN и END.

2. Описание подпрограммы-функции начинается со строки

Здесь:

• Procedure — зарезервированное слово, указывающее транслятору, что далее идёт описание подпрограммы-процедуры;

• <имя процедуры> — идентификатор, выбираемый по тем же правилам, что и для имён переменных;

• сразу после имени функции в скобках записывается перечень передаваемых в эту функцию формальных параметров — имён переменных, которые будут использоваться при вычислениях, выполняемых в процедуре, и имён переменных, в которые процедура должна записать полученные результаты. Формальные параметры (как и в функциях) группируются через запятую в блоки одинаковых типов, а обозначения их типов записываются после списка параметров через двоеточие; блоки параметров различного типа записываются через точку с запятой;

• в процедуру, кроме обычных значений (числовых или символьных), можно передавать данные составных типов (массивы, записи и пр.). Для этого надо объявить такой составной тип, как пользовательский в разделе type в начале программы, далее объявить в разделе var соответствующий экземпляр данных как переменную этого составного типа, а далее при определении процедуры указать для соответствующих формальных параметров этот составной (пользовательский) тип.

Пример:

Procedure Pr1(L : integer; var R : atype ) ; — объявляется процедура с именем Prl, которая работает с целым (тип integer) числом L и массивом R, тип которого (atype) был ранее определён в разделе type:

При этом параметры процедуры могут передаваться в нее как значения или как ссылки. В чем заключается различие между этими двумя способами передачи данных, мы рассмотрим чуть позже. Пока же отметим, что составные данные (в том числе массивы) обычно передаются как ссылки, а признаком передачи ссылки в процедуру является запись служебного слова var перед именем формального параметра (как и сделано в данной программе для передачи в процедуру массива R).

3. После строки определения процедуры записывается её программный код. Правила его записи аналогичны правилам записи основной программы:

• сначала может присутствовать раздел описания локальных констант и переменных, действующих только в пределах данной процедуры;

• далее между операторными скобками begin и end записывается текст подпрограммы.

4. Результаты вычислений, которые процедура должна вернуть в основную программу, должны быть записаны в качестве значения соответствующего формального параметра.

5. В тексте основной программы вызов процедуры производится следующим образом:

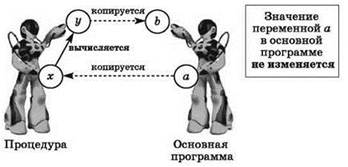
• записывается имя процедуры, а после него в скобках через запятую — список фактических параметров — константы, имена переменных, выражения, а также другие вызовы процедур или функций, значения которых нужно передать в процедуру для выполнения вычислений. Переменные, в которые процедура должна вернуть результаты вычислений, также записываются как её фактические параметры (и это должны быть переменные, объявленные в основной программе!). Количество и типы всех фактических параметров должны соответствовать указанным в объявлении процедуры формальным параметрам. При этом если параметр передаётся как значение, то это значение при вызове подпрограммы будет скопировано в соответствующий формальный параметр, так что если процедура, выполняя вычисления, изменит значение этого формального параметра, то это никак не повлияет на значение “фактической” переменной в основной программе. А вот если параметр передаётся как ссылка, то в процедуру попадёт информация о расположении в оперативной памяти компьютера самих исходных данных (скажем, массива), и тогда все изменения, которые процедура совершит с таким формальным параметром, будут отражены в самом исходном массиве. Иными словами, передавая массив (или другой экземпляр составных данных) в процедуру по ссылке, мы отдаём процедуре всю “власть” выполнять любые изменения с этим массивом. Соответственно, для возвращения результата изменений параметра, переданного как ссылка, не требуется предусматривать какой-то отдельный параметр: все эти изменения сразу производятся в исходном экземпляре данных.

Передача данных как значения

Передача данных как ссылки

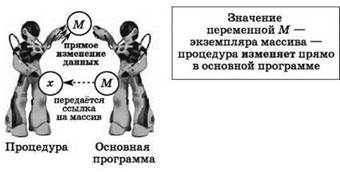
• поскольку процедура возвращает результаты своей работы через свои параметры, она записывается как отдельная команда программы, а не как составная часть выражения или оператора присваивания.

Разбор типовых задач

Задача 1. Определить, какое число будет напечатано в результате работы следующей программы:

Решение

В тексте программы (если не считать подключения модуля crt в разделе uses) вначале объявлен целый ряд переменных (раздел var).

Затем следует описание подпрограммы-функции с именем F, которой должно передаваться одно исходное значение — действительное число (формальный параметр х, который затем используется в качестве переменной в тексте подпрограммы) и которая должна возвращать действительное значение. Что именно вычисляется в этой подпрограмме, пока подробно не рассматривается.

После подпрограммы записан текст основной программы (между BEGIN И END).

Чтобы решить эту задачу нужно произвести полную трассировку используемых в программе переменных. Для этого составляется таблица трассировки. Следует особо отметить, что каждый раз, когда встречается в основной программе вызов функции, нужно переходить к тексту её описания и выполнять соответствующие команды до завершающего текст подпрограммы-функции слова end. При этом заданные в вызове функции фактические параметры автоматически переписываются в таблицу в качестве значений соответствующих им формальных параметров (столбец формального параметра, равно как и команды подпрограммы-функции, в таблице выделен серым фоном ячеек). Для наглядности значения переменных, изменяемые в результате действия текущей команды, выделены жирным шрифтом.

Выполнение полной трассировки такой программы — дело сложное и долгое. Однако можно выявить следующую закономерность: пока с увеличением значения t получаемое значение F(t) также увеличивается (в результате чего это значение каждый раз оказывается больше предыдущего значения F(t), запомненного в переменной R) текущее значение t заносится в интересующую переменную М.

Если выполнить перемножение скобок в выражении, записанном в составе функции F, то получается квадратное уравнение:

Поскольку перед х² стоит знак минуса, ветви параболы, соответствующей этому уравнению, будут направлены вниз. Вычисления производятся по левой ветви этой параболы снизу вверх. Очевидно, что рано или поздно они “доберутся” до вершины параболы, после чего с ростом t начнётся “движение” по её второй ветви уже сверху вниз. Тогда условие F(t) > R перестанет выполняться (это произойдёт, когда будет пройдена вершина параболы и при переходе к следующему же после этого значению t), а значит, прекратится и запись текущих значений t в переменную М. Так будет до самого конца цикла изменения t.

Остаётся найти координату вершины параболы t и проследить работу программы вблизи этого значения данной переменной. Для этого можно использовать тот факт, что в вершине параболы значение производной равно нулю: -2х + 2 = 0. Тогда х = 1. Значит, искомое значение переменной t равно 1. Трассировка продолжается с него.

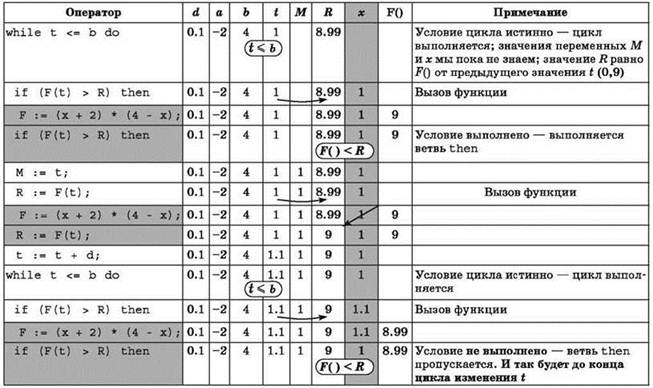
Итак, последнее возможное изменение значения переменной М уже произошло, и при этом М стала равна 1.

Ответ: в результате работы данной программы будет выведено число 1 (вариант № 1).

Задача 2. Определите, какое число будет напечатано в результате работы следующей программы (для вашего удобства программа представлена на четырёх языках):

Бейсик	Паскаль
Си	Алгоритмический язык

1) -1

2) 2

3) -3

4) 24

Решение

Видя сходство предлагаемого текста программы с разобранным в предыдущей задаче, можно упростить решение.

Из текста программы извлекается “ключевая” информация об обрабатываемом графике функции:

• диапазон изменения аргумента функции [а, b] — от -3 до 3;

• шаг изменения аргумента функции d — 0,1;

• формула, определяющая функцию:

F = (х - 1) ∙ (х - 3).

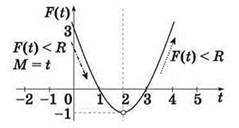
Раскрыв в записи этой функции скобки, получается квадратичная функция (х² - 4х + 4), график которой представляет собой параболу. При этом “нули” этой функции (точки пересечения её графика с осью абсцисс) нетрудно найти из исходной записи функции:

Чтобы определить направление ветвей параболы, нужно определить знаки значений заданной функции в трёх точках, одна из которых расположена внутри интервала между найденными корнями, а две другие — вне этого интервала:

Таким образом, ветви параболы направлены вверх. Вершина параболы (точка её минимума) определяется приравниванием нулю производной заданной функции:

Имеется фрагмент текста программы:

До каких пор будет производиться перезапись значения переменной M?

В предыдущей задаче аналогичный фрагмент листинга содержал условие F (t) > R, и подобная перезапись значений М происходила, пока последующее значение функции оказывалось больше, чем запомненное в переменной R предыдущее, т.е. происходил подъём по графику до точки максимума. В нашем же случае условие обратное: F (t) < R. Оно показывает, что изменение значений М будет происходить, пока последующее значение функции будет меньше предыдущего. Это соответствует спуску до минимальной точки параболы.

Тогда по аналогии с предыдущей задачей можно предположить, что последним перезаписанным значением переменной М будет значение t, соответствующее точке минимума параболы, т.е. 2.

Ответ: в результате работы данной программы будет выведено число 2 (вариант № 2).

В подобных задачах, видя их аналогию, можно упростить решение:

• проанализировать вид графика заданной функции;

• определить, выполняется ли подъём по графику до максимальной точки или спуск до минимальной;

• найти эту максимальную или минимальную точку и записать в качестве ответа соответствующее ей значение аргумента (ж или t).

Однако подобный способ решения — достаточно рискованный, поскольку опирается на предположение, что в условии задачи изменён только вид функции и, возможно, диапазон изменения аргумента. Если составители заданий ЕГЭ поменяют сам алгоритм, то такое “упрощённое” решение будет неверным. Поэтому на реальном ЕГЭ лучше дополнительно провести решение с полной трассировкой программы, показанное в задаче 1.

При решении таких задач, анализируя вид графика заданной функции, следует не забывать проверять, находится ли точка её минимума (максимума) в заданном интервале изменения абсцисс! В противном случае остановка перезаписи значения М произойдёт на границе интервала “на пути” к минимуму/максимуму, поэтому ответом будет значение аргумента на соответствующей границе исходного интервала.

Задача 3. Определите, какое значение Н нужно ввести, чтобы число, напечатанное в результате выполнения следующего алгоритма, было наименьшим.

Решение

В предыдущих задачах требовалось для функции одной переменной F(x), представляющей собой квадратное уравнение, найти, какое число выводится в результате. А здесь — функция с двумя переменными F(H,x), которая представляет собой квадратное уравнение с параметром Н, и искать надо значение этого параметра, такое, чтобы выводимое значение было наименьшим.

Прежде всего, заметим, что работа в языке программирования (в данном случае в Паскале, но это верно и для других языков — по крайней мере для большинства из них) с функциями с одной и с двумя переменными полностью идентична: в обоих случаях в функцию передаются значения переменных, а результат возвращается через саму функцию F(). Поэтому сосредоточимся на собственно решении.

1) Анализируем алгоритм.

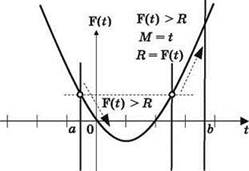
• В цикле идёт перебор значений t от заданных ранее а = -10 до b = 50. При этом в переменной М запоминается сначала начальное значение а, а потом (при срабатывании условного оператора) — текущее значение t, а в переменной R хранится предыдущее значение функции F(H,x).

• Если с увеличением значения t получаемое значение F() увеличивается (и в результате оказывается больше предыдущего значения F(t), запомненного в переменной R), текущее значение tзаносится в переменную М, а значение функции в этой точке запоминается в R.

• До каких пор это будет продолжаться? Посмотрим на выражение, записанное в составе функции F(). Выполним в нём перемножение скобок. Получим:

Это — явно запись квадратного уравнения (если приравнять это выражение нулю), графиком которого является парабола. Поскольку перед х² стоит знак “плюс”, ветви этой параболы направлены вверх. И мы в своих вычислениях “движемся” по левой ветви этой параболы сверху вниз. Значит, условный оператор в цикле не будет работать до тех пор, пока мы не пройдём вершину параболы (минимум на её графике) и не поднимемся по правой ветви настолько, что значение выражения 11t² – 22tH + (11Н² +13) (замена переменной х на t происходит при переходе из основной программы в функцию) в некоторой точке t превысит его значение в исходной точке а. А после этого, пока мы “движемся” по правой ветви параболы вверх, у нас значение R будет всё расти вплоть до окончания цикла по достижении точки b (см. примерный рисунок). Следовательно, конечное значение R будет равно значению выражения F(H,b) = 11b² – 22bН + (11Н² + 13) либо, если расположить параболу так, что указанное значение меньше чем исходное (F(H,a) = 11a² - 22aH + (11Н²+13)), значение к будет равно этому исходному.

2) Как нужно расположить параболу, чтобы получить минимально возможное значение R? И каким оно будет? Очевидно, что если ветвь then начнёт работать, то это приведёт к увеличению значения R. Следовательно, наименьшее значение R (которое и выводится на экран в результате работы программы), будет достигаться, если ветвь then так ни разу и не сработает (и будет равным значению в исходной точке а). Для этого требуется, чтобы в точках а = -10 и b = 50 значения выражения, записанного в функции, были равными:

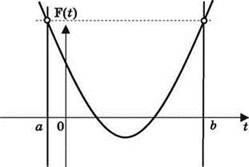
3) Остаётся вычислить значение Н такое, чтобы получить нужное расположение параболы. Для этого надо составить уравнение в виде:

или, подставляя известные нам значения а = -10 и b = 50:

Очевидно, одинаковые слагаемые (11Н² + 13) сразу сокращаются. Также можно разделить обе его части на 11. Получаем уравнение первого порядка:

Решаем его:

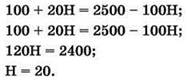
Ответ: 20.

Задача 4. Имеется следующий рекурсивный алгоритм:

Чему равна сумма чисел, выведенных на экран при вызове F(2)?

Решение

Наиболее универсальным способом решения таких задач является построение “дерева вызовов” функции с последующим подсчётом суммы чисел на концах его “ветвей”. Для этой задачи такая схема “по шагам” будет такой:

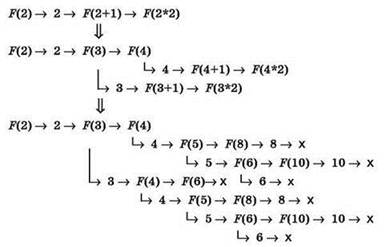
Далее остаётся просуммировать числа, которые выводятся на экран при работе данного алгоритма (и которые в нашем “дереве” выделены рамкой. Эта сумма равна 2+4+8+5+10+6+3+6+4+8+5+10+6 = 77.

Однако даже для такой несложной задачи “дерево вызовов” получается довольно громоздкое, и к тому же при его рисовании требуется внимательность, чтобы ничего не упустить (а особенно — не забыть, что даже если очередное значение n уже не удовлетворяет условию в операторе if, значение п все равно выводится на экран, так как соответствующий оператор располагается до условного оператора) и просуммировать все полученные числа. Как показала практика, с рисованием таких “деревьев” справляются далеко не все учащиеся.

Взамен рисования “дерева вызовов” можно предложить метод решения, который можно назвать “алгебраическим”. Он работает для таких задач, в которых в рекурсивной функции сначала стоит оператор if с условием “n меньше некоторого граничного значения”, а в ветви then этого if записаны рекурсивные вызовы функции F с аргументом, изменяющимся в большую сторону, причём оператор вывода значения n стоит перед if и может также иметься в ветви then.

В отличие от “дерева вызовов”, здесь мы решаем задачу “наоборот”, в порядке, противоположном нормальной работе рекурсивного алгоритма. Начинаем запись с последнего натурального числа, которое ещё удовлетворяет условию в операторе if. В данном случае это условие имеет вид n < 6, поэтому начинаем запись с числа 5.

При этом цветом выделяем число, выводимое на экран.

Для записи вызовов функции F() в строку записываем или ранее вычисленное значение для этой функции (если оно есть), или просто число, получаемое в качестве аргумента функции.

В последней записи должно быть то число, которое задано в вызове (в данном случае — число 2).

Ответ: 77.

Задача 5. Имеется следующий рекурсивный алгоритм:

Чему равна сумма чисел, выведенных на экран при вызове F(2)?

Решение

Основное усложнение — в том, что в алгоритме есть два оператора вывода: один — вне if, второй — в его ветви then. Однако принцип формирования записей остается тот же, хотя к таблице добавляется ещё одна отдельная графа: теперь в “основной” части таблицы мы записываем расчёты для “внутренних” операторов (в ветви then оператора if), а затем в отдельной графе записываем расчёты для отдельного оператора вывода вне if.

1. Часть внутри if. Условие имеет вид n < 7, поэтому начинаем запись с числа 6. Выделяем число, выводимое на экран. Для записи вызовов функции F() в строку записываем или ранее вычисленное значение для этой функции (если оно есть), или просто число, получаемое в качестве аргумента функции. В последней записи должно быть число, которое задано в вызове (в данном случае — число 2).

2. Часть вне if. В каждой строке записи сначала записывается само число, которое выводится на экран внешним оператором вывода. Затем мы смотрим на соответствующую этому числу “основную” запись F(): если в ней задействованы ранее вычисленные значения F(n), то к выведенному на экран числу прибавляются значения, вычисленные нами в “дополнительной” графе для этих F(n).

В итоге нужно сложить значение, полученное в последней записи “основной” графы, и значение, полученное в последней записи “дополнительной” графы.

n	Внутри if	Вне if
6		6
5		5 + 6 = 11 (шестерка “пришла” сюда через вызов F(6))
4		4 + 11 + 6 = 21 (число 11 “пришло” через вызов F(5), число 6 — через вызов F(6))
3		3 + 21 + 11 + 6 = 41 (число 21 — через вызов F(4), 11 — через вызов F(5), 6 - через F(6))
2		2 + 41 + 21 + 21 = 85 (число 41 — через вызов F(3), 21 — через вызов F(4))
ИТОГ:	F(2) = 393 + 85 = 478.

Задача 6. В программе содержатся две рекурсивные функции F и G:

Чему равно значение, вычисленное при выполнении вызова F(8)?

Решение

Отрабатываем программу для n = 8. При этом таблицу трассировки удобнее строить из двух частей (соответствующих вызовам F(n) и G(n)) и решать задачу в два прохода — сначала на прямом проходе мы только записываем вызовы функций, а затем на обратном проходе, в обратном порядке снизу вверх, записываем получаемые значения.

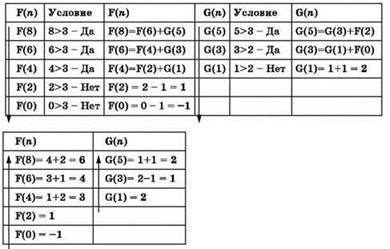
Ответ: 6.

Другой возможный вариант решения — построение дерева вызовов функций, однако этот способ решения более громоздкий.

Задача 7. Определите количество различных значений входной переменной k, при которых программа выдаёт тот же ответ, что и при входном значении k = 64. Значение k = 64 также включается в подсчёт.

В новых задачах такого типа выражение, записанное в подпрограмме-функции, может быть любым, а цикловая переменная может как уменьшаться, так и увеличиваться, но принцип решения таких задач остаётся тем же. В любом случае первое неравенство составляется для значения i, при котором цикл ещё выполняется (последний раз), и в нём записывается в точности такой знак неравенства, как в условии цикла. Второе неравенство составляется для значения i, при котором цикл уже не выполняется, и знак этого неравенства — противоположный первому (в том числе по строгости/нестрогости).

Решение (первый способ)

1) Анализируем алгоритм. Функция используется здесь только для выполнения вычислений, поэтому для упрощения анализа программы можно записать соответствующее выражение прямо взамен вызова функции:

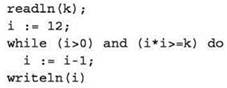
2) Теперь выполним трассировку программы для заданного значения k = 64:

i	i * i	Условие	k
12	144	12 > 0; 144 ≥ 64	64
11	121	11 > 0; 121 ≥ 64
10	100	10 > 0; 100 ≥ 64
9	81	9 > 0; 81 ≥ 64
8	64	8 > 0; 64 ≥ 64
7	49	7 > 0; 49 < 64

Обратите внимание: при i = 8 условие выполнения цикла всё ещё истинно, поэтому в теле цикла в последний раз выполняется уменьшение значения переменной i. Но сразу после этого условие цикла становится ложным, выполнение цикла прекращается, а на экран выводится уменьшенное на 1 значение i, равное 7.

Итак, для k = 64 будет выведено число 7.

3) Если увеличить значение k на единицу, то при i = 8 получаем:

i	i * i	Условие	k
9	81	9 > 0; 81 ≥ 65	65
8	64	8 > 0; 64 < 65

То есть условие цикла будет нарушено уже при i = 8 (на экран вместо числа 7 будет выведено число 8). То же будет и при дальнейшем увеличении k. Следовательно, k = 64 — это наибольшее возможное значение.

4) А что будет, если уменьшать k? Очевидно, что программа будет работать так же, как и при k = 64, пока k не станет равно 49 (т.е. значению функции f при i = 7). В этом случае программа будет работать следующим образом:

i	i * i	Условие	k
12	144	12 > 0; 144 ≥ 49	49
11	121	11 > 0; 121 ≥ 49
10	100	10 > 0; 100 ≥ 49
9	81	9 > 0; 81 ≥ 49
8	64	8 > 0; 64 ≥ 49
7	49	7 > 0; 49 ≥ 49
6	36	6 > 0; 36 < 49

В результате на экран вместо числа 7 будет выведено число 6.

Следовательно, уменьшать значение k можно только до 50.

5) Делаем вывод: программа работает одинаково (с выводом на экран числа 7) при значениях k из интервала от 50 до 64. Таких значений — (64 - 50 + 1) = 15 (единица прибавляется, так как мы определяем количество чисел в диапазоне, в который входят обе его границы).

Решение (второй способ)

1) Так же, как и в предыдущем случае, начинаем с трассировки программы. Это позволяет определить “граничные” значения i: последнее, при котором цикл ещё выполняется (i = 8) и первое, при котором цикл перестаёт выполняться (i = 7).

2) В соответствии с этим записываем два неравенства, левые части которых представляют собой выражение из условия цикла (оно же — выражение, записанное в теле функции f) с подстановкой найденных значений i, а в правых частях записывается переменная k:

• 8*8 ≥ k (так как при i = 8 это условие цикла истинно);

• 7*7 < k (так как при i = 7 условие i*i ≥ k ложно, поэтому знак в нём меняется на противоположный с заменой нестрогого неравенства на строгое).

3) Получаем систему неравенств и решаем её:

4) Решением этой системы неравенств является интервал k = (49,64]. Обратим внимание на то, что в этом интервале левая граница в него не входит (соответствующее неравенство — строгое).

5) Определяем количество значений k, входящих в этот интервал. Оно равно (64 - 49) = 15.

Ответ: 15.

Задача 8. Определите наименьшее возможное значение входной переменной х, при котором программой будет получен ответ 31.

Решение

1. Учитывая, что функции f(i) и g(i) не обращаются друг к другу, можно просто подставить соответствующие выражения в основную программу вместо вызова этих функций:

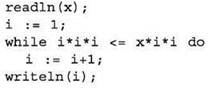
2. Очевидно, что вывод результата 31 означает, что выполнение цикла while будет остановлено, когда условие 31³ ≤ х ∙ 31² ложно, хотя условие 30³ ≤ х ∙ 30² все ещё истинно.

Тогда можно получить следующую систему неравенств:

3. Решаем эту систему неравенств:

Решение очевидно: х = 30.

Ответ: 30.