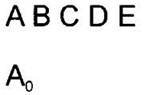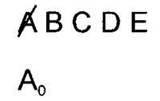Информатика - Новый полный справочник для подготовки к ОГЭ
Графическое представление информации - Проектирование и моделирование - ИНФОРМАЦИОННЫЕ И КОММУНИКАЦИОННЫЕ ТЕХНОЛОГИИ
Конспект
Введение
Достаточно часто для представления информации о связях между объектами, процессами или явлениями используют графические способы представления информации. Одним из весьма распространенных графических способов является граф.
Формально граф — это совокупность некоторого количества объектов (обычно называемых вершинами) и соединяющих их связей (обычно называемых рёбрами). Без сомнения, вы много раз видели графы. Обычно в виде графов рисуют схемы метрополитена, железных дорог/электричек или городов и связывающих их дорог.
Итак, ещё раз более простыми словами. Граф состоит из некоторого количества вершин (называемых также узлами или пунктами). В привычных для нас перечисленных выше схемах вершинами графа являются станции или населённые пункты. Соединяющие их связи — это дороги между станциями/населёнными пунктами. Их, как мы уже упомянули, называют рёбрами графа.
Для того, чтобы описать, как вершины графа соединяются рёбрами, применяют либо графический, либо табличный способы. Графический способ весьма наглядный, именно его мы представляем себе, когда работаем с графом. Но для обработки информации о графе на компьютере такой способ представления графа (в виде рисунка) чаще всего неудобен. При обработке на компьютере используют обычно какой-нибудь из табличных способов. Один из самых популярных табличных способов — так называемая матрица смежности. Пусть вас не пугают эти слишком заумные слова — “матрица” и “смежности”. Матрица — в данном случае всего лишь квадратная таблица. Смежность — представление о том, существует ли ребро между парой вершин (то есть, являются ли они соседними — смежными). В этой матрице-таблице столько строк и столбцов, сколько вершин в графе. На пересечении строки номер X и столбца номер Y хранится число 0 или 1. Число 1 — если существует связь (ребро) между вершинами X и Y. Число 0 — если такого ребра не существует.
Пример графа и соответствующей ему матрицы смежности.
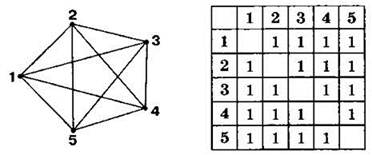
В действительности, правильнее сказать, что на пересечении строки X и столбца Y записано количество рёбер, которые выходят из вершины X и входят в вершину Y. Отличие этого определения от того, что мы привели чуть выше, оказывается в случае, когда из вершины X в вершину Y идёт более одного ребра. Либо в случае, когда ребро из вершины X в вершину Y есть, а в обратную сторону (из вершины Y в вершину X) такого ребра нет.
Деревья
В случае, если в графе из любой вершины в любую другую можно добраться единственным образом, граф можно считать деревом. Другое определение дерева — это граф, в котором отсутствуют циклы. То есть, нельзя “выйти” из какой-либо вершины дерева и, проходя по любому ребру не более одного раза, вернуться обратно в ту же вершину.
Когда все рёбра дерева имеют направления (по ним можно двигаться только в направлении, указанном стрелкой), дерево называется направленным (или ориентированным). В дальнейшем мы будем пользоваться только направленными деревьями, хотя и не будем для простоты рисовать на каждом ребре стрелку.
В направленном дереве выделяют специальную вершину — корень дерева. Это вершина, в которую не входит ни одно ребро. А также часть вершин называют листьями. Это вершины, из которых не выходит ни одного узла. Если из вершины выходит хотя бы одно ребро, вершина называется узлом дерева. Заметим, что корень дерева так же является узлом дерева.
Обычно деревья (структуры данных) рисуют сверху вниз или слева направо. То есть, корень дерева располагается сверху, а ветви направлены вниз, либо корень дерева располагается слева, а ветви направлены вправо.
Таблица расстояний
В ряде случаев при помощи графа требуется отобразить не только наличие связей между вершинами, но и расстояния между ними. Например, расстояния между соседними населёнными пунктами по дорогам.
При изображении графа в виде рисунка эти расстояния просто указываются прямо на рёбрах.
При хранении графа в табличном виде обычно используют таблицу расстояний. В ней на пересечении строки X и столбца Y записано число, которое показывает длину ребра из вершины X в вершину Y. Если из вершины X в вершину Y нет ребра, клетка в таблице остаётся пустой.
При обработке программным образом ячейки таблицы, для которых не существует соответствующего ребра, хранят обычно очень большое число, которое никак не влияет на алгоритм поиска в таблице. Либо хранят отрицательное число, которое алгоритм проверяет, чтобы понимать существование или не существование ребра.
Пример графа с подписанными длинами рёбер и соответствующая ему таблица расстояний:

Одной из весьма распространённых задач обработки графов является задача поиска кратчайшего расстояния между двумя вершинами (например, населёнными пунктами). Обычно граф при этом задан таблицей расстояний.
Разбор типовых задач
Задача 1. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице.
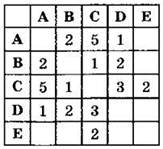
Определить длину кратчайшего пути между пунктами А и Е.
Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Решение
Для решения этой задачи воспользуемся специальным алгоритмом, который эффективно решает именно такого вида задачу — находит кратчайшее расстояние на графе от одной вершины до другой. Этот алгоритм называется алгоритмом Дейкстры. Побочным эффектом алгоритма Дейкстры является нахождение кратчайшего расстояния от некоторой стартовой вершины до всех остальных вершин графа. Но это никоим образом не ухудшает его качества — алгоритм Дейкстры ищет кратчайшее расстояние быстро, надёжно и эффективно.
|
0. Выпишем в отдельный список все возможные вершины графа. |
|
|
1. Будем строить дерево. Нарисуем стартовую вершину (в нашем случае это точка А) и подпишем рядом с ней расстояние, которое нужно “проехать”, чтобы добраться до неё из стартовой точки А. То есть, 0. Эта вершина будет корнем нашего дерева. |
|
|
2. Из всех возможных листовых вершин дерева найдём вершину с наименьшим числом (в данном случае, такая вершина только одна — А). Вычеркнем эту вершину из списка доступных вершин. В дальнейшем её мы больше не будем рассматривать в качестве возможной вершины дерева. То есть, вычеркнутые вершины в дерево больше не дорисовываются! Расстояния от стартовой вершины до них подсчитаны окончательные и лучше уже не будут. Следующее действие будем делать из этой вершины. |
|
|
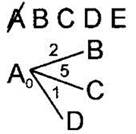
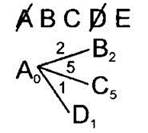
3. По таблице расстояний найдём все вершины, до которых идёт ребро из текущей вершины (сейчас это вершина А) и которые ещё не вычеркнуты. Это вершины В, С, D. Нарисуем из текущей вершины (А) ветви дерева для каждой из найденных смежных вершин. На концах ветвей укажем названия этих вершин. На ветвях подпишем длины рёбер по таблице расстояний. |
|
|
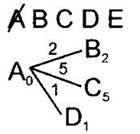
4. Для каждой полученной вершины посчитаем расстояние до неё как: расстояние до текущей вершины (подписано рядом с ней, сейчас для вершины А это 0) плюс расстояние (длина ребра) до каждой полученной вершины (подписано над ребром). Запишем эти расстояния рядом с каждой полученной вершиной. |
|
|
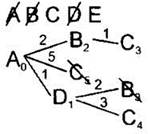
5. Среди листовых вершин найдём вершину с наименьшим расстоянием. В данном случае это вершина D. Вычеркнем эту вершину из списка доступных вершин. Дальнейшие действия будем делать из неё. Это такое же действие, как действие 2. |
|
|
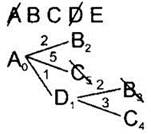
6. По таблице расстояний найдём все вершины, до которых идёт ребро из текущей вершины (сейчас это вершина D) и которые ещё не вычеркнуты. Это вершины В и С. Нарисуем из текущей вершины (D) ветви дерева для каждой из найденных смежных вершин, нарисуем на концах ветвей названия этих вершин. Подпишем на ветвях длины рёбер по таблице расстояний. Это такое же действие, как действие 3. |
|
|
7. Для каждой полученной вершины посчитаем расстояние до неё как: расстояние до текущей вершины (подписано рядом с ней, сейчас для вершины D это 1) плюс расстояние (длина рёбра) до каждой полученной вершины (подписано над ребром). Запишем эти расстояния рядом с каждой полученной вершиной. Это такое же действие, как действие 4. |
|
|
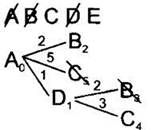
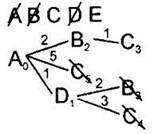
8. Среди всех листовых вершин будем искать одинаковые вершины. Сейчас это пара вершин В2 и В3 и пара вершин С5 и С4. Для каждой пары одинаковых вершин будем вычеркивать в дереве худшую вершину. То есть, вершину с большим расстоянием до неё. Сейчас это В3 и С5. Если в паре одинаковых вершин расстояния будут одинаковые, нужно вычеркнуть одну любую. Мы специально вычеркиваем вершины указанным образом (от левого верхнего к правому нижнему углу), чтобы перечеркнуть как название вершины, так и расстояние до неё. Это облегчит в дальнейшем поиск вершины с наименьшим расстоянием. Заметим, такого действия (вычеркивания) мы раньше не делали, потому что у нас ещё не встречались одинаковые вершины. В действительности, это часть циклического алгоритма. Действия 5-8 будем повторять, пока не вычеркнем конечную вершину из списка доступных вершин. |
|
|
9. Среди листовых вершин найдём вершину с наименьшим расстоянием. В данном случае это вершина В. Вычеркнем эту вершину из списка доступных вершин. Дальнейшие действия будем делать из неё. |
|
|
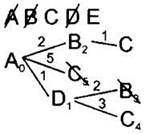
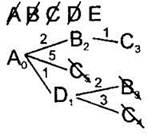
10. По таблице расстояний найдём все вершины, до которых идёт ребро из текущей вершины (сейчас это вершина В) и которые ещё не вычеркнуты. Это вершина С. Нарисуем из текущей вершины (В) ветви дерева для каждой из найденных смежных вершин, нарисуем на концах ветвей названия этих вершин. Подпишем на ветвях длины рёбер по таблице расстояний. |
|
|
11. Для каждой полученной вершины посчитаем расстояние до неё как: расстояние до текущей вершины (подписано рядом с ней, сейчас для вершины В это 2) плюс расстояние (длина ребра) до каждой полученной вершины (подписано над ребром). Запишем эти расстояния рядом с каждой полученной вершиной. Сейчас это С3. |
|
|
12. Среди всех листовых вершин будем искать одинаковые вершины. Сейчас это С3 и С4. Для каждой пары одинаковых вершин будем вычеркивать в дереве худшую вершину. То есть, вершину с большим расстоянием до неё. Сейчас это С4. |
|
|
13. Среди листовых вершин найдём вершину с наименьшим расстоянием. В данном случае это вершина С. Вычеркнем эту вершину из списка доступных вершин. Дальнейшие действия будем делать из неё. |
|
|
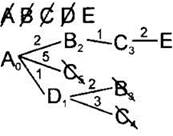
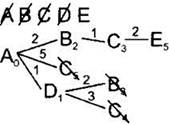
14. По таблице расстояний найдём все вершины, до которых идёт ребро из текущей вершины (сейчас это вершина С) и которые ещё не вычеркнуты. Это вершина Е. Нарисуем из текущей вершины (С) ветви дерева для каждой из найденных смежных вершин, нарисуем на концах ветвей названия этих вершин. Подпишем на ветвях длины рёбер по таблице расстояний. |
|
|
15. Для каждой полученной вершины посчитаем расстояние до неё как: расстояние до текущей вершины (подписано рядом с ней, сейчас для вершины С это 3) плюс расстояние (длина ребра) до каждой полученной вершины (подписано над ребром). Запишем эти расстояния рядом с каждой полученной вершиной. Сейчас это Е5. |
|
|
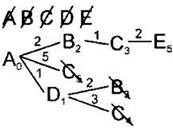
16-17. Среди всех листовых вершин будем искать одинаковые вершины. Сейчас таких пар нет. Среди листовых вершин найдём вершину с наименьшим расстоянием. В данном случае это вершина Е. Вычеркнем эту вершину из списка доступных вершин. Это конечная вершина, расстояние до которой мы искали. Алгоритм закончен. Ответ: 5. |
|
Несколько замечаний относительно применения приведённого алгоритма.
Несмотря на ощущение объёма и громоздкости, которые могли возникнуть при изучении этого алгоритма, алгоритм выполняется просто и быстро.
Обратите внимание на количество записей, которые нужно сделать для его выполнения на черновике (это то, что приведено в правом столбце таблицы в последней строке). Всего несколько букв, линий и цифр. Выполняются они очень легко. Освоив эти действия, выполнение их надёжно приводёт к правильному результату.
Хотелось бы предостеречь вас от ощущения того, что правильный ответ гораздо быстрее найти, просто анализируя таблицу расстояний и перебирая всего несколько вариантов. Зачастую это, действительно, так. Но перебирание в уме нескольких вариантов может привести к потенциальным ошибкам. Запись промежуточных действий на черновике позволяет отследить ряд ошибок, используя не только устные рассуждения, но и визуальный контроль своих действий.
Ещё одной альтернативой приведённого алгоритма является построение по таблице расстояний исходного графа. По построенному графу уже можно визуально (или “водя пальцем”) быстро найти нужный ответ.
Заметим, что время, затраченное на построение графа, сравнимо со временем построения дерева алгоритма Дейкстры. Однако, алгоритм Дейкстры даёт гораздо более надёжный результат.
Также выделим, что зачастую при решении задачи у вас есть возможность делать заметки прямо на условии (как, например, на экзамене, к которому мы с вами готовимся).
В этом случае не нужно заранее выписывать список доступных вершин. Удобнее использовать сразу верхнюю строчку таблицы расстояний, где все вершины сразу перечислены. Вычеркивание вершин рекомендуется делать сразу в этой таблице. Это экономит немного времени. Ещё это удобно тем, что при поиске в таблице расстояний тех вершин, которые смежны с текущей и не являются уже вычеркнутыми, сразу видны вычеркнутые вершины.
В нашем примере это были шаги алгоритма 3, 6, 10, 14.
Количество путей на графе
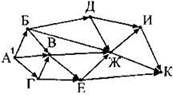
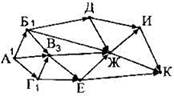
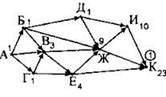
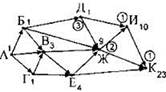
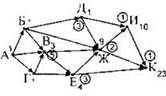
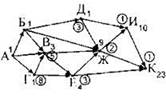
Задача 2. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
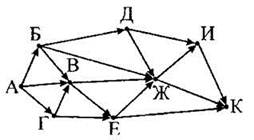
Решение
Традиционный на первый взгляд метод решения этой задачи — водить пальцем по схеме от города к городу и подсчитывать, сколькими различными способами это можно сделать.
Этот способ по надёжности не выдерживает никакой критики — пропустить один или несколько вариантов очень легко, а проверить себя при этом практически невозможно.
Для решения воспользуемся быстрым и эффективным способом решения под названием динамическое программирование. Пусть вас не смущает слово программирование. Никакого программирования при этом не будет. Просто способ используется в программировании при решении ряда подобных или похожих по принципу решения задач. Идея метода динамического программирования состоит в том, чтобы постепенно, шаг за шагом, получать частичные результаты для каждой рассматриваемой вершины. В результате работы метода на последнем шаге мы получим ответ для искомой вершины. В данном случае интересующий нас результат — это сколькими различными способами можно “доехать” из стартового города до текущей вершины (города).
|
Будем последовательно искать, сколькими различными способами можно добраться из города А до каждого из городов, нарисованных на схеме. Прежде всего, для выполнения нужного нам решения необходимо понять, сколькими способами можно добраться из города А до самого города А. Важно понимать, что это возможно осуществить только одним способом. Не нулём, как могло бы показаться поначалу, а именно одним способом — никуда не уезжая. Пометим вершину А числом 1 (количество способов, которым можно добраться до данной вершины). |
|
|
Теперь постараемся пометить какую-нибудь ещё вершину. Это можно сделать только для тех вершин, про которые известно нужное количество всех стрелок, входящих в данную вершину. На данном этапе нам известно это нужное количество только для вершины — А. Значит, будем искать вершины, в которые входит только одна стрелка дороги — из вершины А. Таких городов на данной схеме два — Б и Г. Пометим их числами 1. Это количество способов добраться из города А в города Б и Г. |
|
|
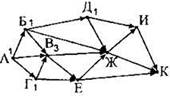
Опять будем искать город, про который для всех стрелок, входящих в него, на схеме уже написаны числа. Один из таких городов — город В. В него входит три стрелки. Для каждой из стрелок (из городов А, Б, Г) уже написаны числа. Нужное число для текущего города В — это сумма чисел на начальных сторонах стрелок. То есть, в город В можно прийти только по трём дорогам-стрелкам из города А, Б или Г. В каждый из них можно прийти одним способом. Значит, в город В можно прийти тремя способами. Пометим город В числом 3. |
|
|
Найдём следующий город, для которого известны числа на началах всех входящих в него стрелках. Один из таких городов — Д. В него входит только одна стрелка из города Б. Значит, в город Д можно добраться столькими же способами — одним. Пометим город Д числом 1. |
|
|
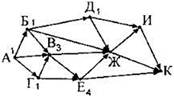
Найдём следующий город, про который известны числа из всех сходящих стрелок. На данном этапе это только один город — Е. В него входит две стрелки-дороги (В и Г). Из города В — 3 способа, из города Г — 1 способ. Всего 4 способа. Пометим город Е числом 4. |
|
|
Ищем следующий город. На данном этапе это город Ж. В него входит 4 дороги. Про все эти стрелки-дороги известны числа для городов, из которых исходят стрелки. Это города Д, Б, В, Е. Рядом с ними написаны числа 1, 1,3,4. Сумма чисел — 9. Это количество способов (9) подписываем рядом с городом Ж. |
|
|
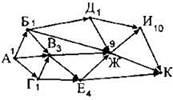
Ищем следующий город. Это город И. В него входит две дороги — из города Д и города Ж. Рядом с ними написаны числа 1 и 9. Их сумма — 10. Это количество напишем рядом с городом И. |
|
|
Последний город, для которого осталось посчитать нужное количество способов — город К. В него входит три стрелки-дороги (из городов И, Ж, Е). Рядом с ними написаны числа 10, 9, 4. Их сумма — 23. Это количество пишем рядом с городом К. Это и является ответом. |
|
Приведённый алгоритм простой и эффективный. Однако при его выполнении можно легко сделать ошибку в арифметических вычислениях или случайно пропустить какую-нибудь стрелку, входящую в вершину. Необходимо сделать проверку.
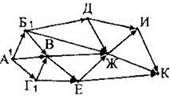
Выполним тот же алгоритм в обратную сторону. То есть, теперь будем искать количество способов, которыми можно добраться из каждого города, обозначенного на схеме, до города К.
|
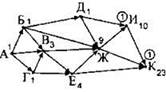
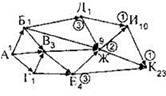
Прежде всего, обозначим количество способов, которым можно добраться из вершины К в вершину К. Как и ранее, это количество равно 1. Подпишем это число (1) возле города К. Но, чтобы не перепутать числа обратного алгоритма с числами прямого алгоритма, будем обводить кружком числа обратного алгоритма. |
|
|
В прямом алгоритме мы искали все города, для которых были известны числа на началах всех входящих стрелок. Теперь будем искать города, для которых известны числа для всех исходящих стрелок. На данном шаге нас устроят только города, из которых выходит только одна стрелка — в город К. Такой город один — город И. Подпишем рядом с ним число 1 в кружке. |
|
|
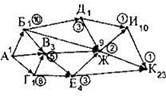
Теперь будем искать города, из которых все исходящие стрелки ведут в города с кружочками. Такая вершина одна — Ж. Из неё идут две стрелки — в города И и К. Рядом с ними в кружках написаны числа 1 и 1. Их сумма — 2. Подпишем рядом с вершиной Ж число 2 в кружке. |
|
|
Ищем следующий город. Один из городов, у которого каждая исходящая стрелка приходит в город с кружком — город Д. Из него выходит две стрелки (в города Ж и И). Числа на концах стрелок — 2 и 1. Их сумма — 3. Пишем число 3 в кружке рядом с городом Д. |
|
|
Следующий город — город Е. Из него выходит две стрелки (в города Ж и К). Числа в кружках на концах стрелок — 2 и 1. Их сумма — 3. Пишем число 3 в кружке рядом с городом Е. |
|
|
Теперь можно посчитать число вариантов для города В. Из него выходит две стрелки (в города Е и Ж). Числа в кружках на концах стрелок — 3 и 2. Их сумма — 5. Пишем число 5 в кружке возле города В. |
|
|
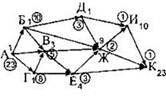
Теперь можно посчитать число вариантов для городов Б и Г. Начнём, например, с города Г. Из него выходит две стрелки (в города В и Е). Числа в кружках на концах стрелок — 5 и 3. Их сумма — 8. Пишем число 8 в кружке возле города Г. |
|
|
Теперь посчитаем число вариантов для города Б. Из него выходит три стрелки-дороги (в города В, Ж, Д). Числа в кружках на концах стрелок — 5, 2, 3. Их сумма — 10. Пишем число 10 в кружке возле города Б. |
|
|
Наконец, можно посчитать число вариантов для города А. Из него выходит три стрелки-дороги (в города Б, В, Г). Числа в кружках на концах стрелок — 10, 5, 8. Их сумма — 23. Пишем число в кружке возле города А. Это ответ. Результаты прямого и обратного алгоритма совпали. Значит, наш ответ — правильный. |
|
Настоятельно рекомендуем при решении этой задачи выполнять оба алгоритма — прямой и обратный — и сверять результаты их работы. Если результаты не совпадут — искать ошибку в обоих алгоритмах. Начинать искать ошибку следует с того алгоритма, результат которого дал меньшее число. Эта рекомендация дана на основании наиболее частой ошибки — забыть добавить в сумму какое-нибудь из чисел или не заметить одну из стрелок. Поэтому, как правило, меньший результат — неверный. Это не значит, что нужно сразу принять за верный ответ большее из двух результатов. Просто рекомендуется начать поиск ошибки с меньшего результата. Для принятия решения о том, что найденный ответ — верный, результаты двух алгоритмов должны совпасть.