Умножение десятичных дробей - Урок 4 - УМНОЖЕНИЕ И ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ - ДРОБНЫЕ ЧИСЛА

Основная дидактическая цель урока: формировать умения умножать десятичные дроби, выполнять умножение десятичных дробей на 0,1; 0,01; 0,001.

Ход урока

I. Организационный момент. Определение темы урока

Сегодня на уроке мы продолжаем работу над темой “Умножение десятичных дробей”.

II. Устный счет

1. Индивидуальная работа у доски.

Задание 1. Выполните умножение.

36,017 ∙ 5,7 = 205,2969

Задание 2. Выполните деление.

170,1 : 45 = 3,78

Задание 3. Найдите значения выражений.

4,56 ∙ 0,1 = 0,456

76,1 ∙ 0,01 = 67,767

3,1 ∙ 0,001 = 0,0031

2. Фронтальная работа (учащиеся работают вместе с учителем).

1) Сторона квадрата 3 см. Найдите периметр, площадь.

2) Длина прямоугольного участка 9 м, а его ширина 6 м. Найдите площадь этого участка.

3) У какой фигуры больше площадь — у квадрата со стороной 8 см или у прямоугольника, длина которого 16 см, а ширина 4 см? (Площади этих фигур равны.)

4) Ребро куба равно 3 см. Найдите площадь боковой поверхности куба. (36 см².)

5) Какую часть площади поверхности всего куба составляет площадь боковой поверхности? (4/6.)

6) Найдите площадь всей поверхности куба. (54 см².)

7) Вычислите объем этого куба. (27 см³.)

3. Коллективная проверка индивидуальной работы у доски.

III. Работа по теме урока

1. Работа в тетради.

(Учитель показывает карточки с выражениями, учащиеся молча записывают только ответы (возможно использование слайдов презентации).)

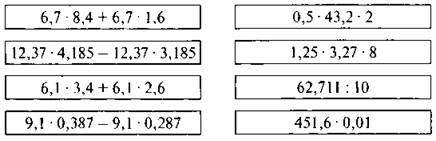
Проверка

(Ответы даны по столбикам.)

67; 12,37; 36,6; 0,91; 43,2; 32,7; 6,2711; 4,516.

2. С. 216, № 1405.

— Прочитайте задание.

— Какие свойства умножения используются при упрощении выражений?

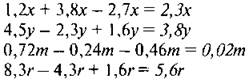
3. С. 216, № 1406 (а, б).

— Прочитайте задание.

— Что нужно сделать перед началом вычисления? (Упростить.)

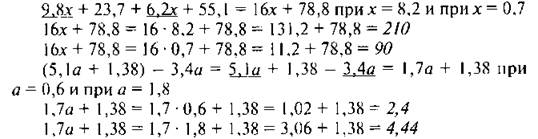
IV. Повторение изученного материала

1. С. 216, № 1408.

— Как вы понимаете выражение “сумма площадей стен”? (Площадь боковой поверхности.)

(Для того чтобы учащимся легче было представить, можно выполнить рисунок на доске.)

— Что можно сказать про площади стен, лежащих напротив друг друга?

— Запишите решение задачи выражением. (2,69 ∙ 3,5 + 2,69 ∙ 3,5 + 6,4 ∙ 2,69 + 6,4 ∙ 2,69.)

— Какой множитель повторяется в каждом произведении?

— Какое свойство умножения мы можем применить?

(3,5 + 3,5 + 6,4 + 6,4) ∙ 2,69 = 19,8 ∙ 2,69 = 53,262 (м²) — объем комнаты.

— Посмотрите на выражение в скобках. Что обозначает число 19,8 м?

— Округлите объем до десятых. (53,262 м² ≈ 53,3 м².)

— Как вы думаете, когда возникает необходимость вычисления площади поверхности стен? (Например, для того, чтобы рассчитать количество краски, обоев для ремонта.)

2. С. 216, № 1409 (работа в паре).

(В ходе анализа данных записывается краткое условие задачи.)

— Найдите объем.

— Что сказано про высоту?

— Как вычислить высоту?

— Что говорится о длине?

— Как найти длину?

— Составьте план решения задачи.

— Решите задачу.

1) 0,4 ∙ 1,5 = 0,6 (дм) — высота параллелепипеда.

2) 0,6 ∙ 1,5 = 0,9 (дм) — длина параллелепипеда.

3) 0,6 ∙ 0,9 ∙ 0,4 = 0,216 (дм³) — объем параллелепипеда.

V. Самостоятельная работа

Вариант 1

С. 219, № 1430 (1).

Решите задачу алгебраическим способом.

Проверка

Пусть второе число будет x.

Тогда первое число будет x + 3,7.

Сумма этих чисел равна x + x + 3,7.

А по условию сумма равна 15,9.

Значит, можем составить уравнение:

x + x + 3,7 = 15,9

2x + 3,7 = 15,9

2x = 15,9 - 3,7

2x = 12,2

x = 12,2 : 2

x = 6,1 — второе число.

15,9 - 6,1 = 9,8 — первое число.

Вариант 2

С. 219, № 1430 (2).

Решите задачу алгебраическим способом.

Проверка

Пусть первое число будет x.

Тогда второе число будет x + 5,4.

Сумма этих чисел равна х + x + 5,4.

А по условию сумма равна 19,8.

Значит, можем составить уравнение:

х + х + 5,4 = 19,8

2х + 5,4 = 19,8

2х = 19,8 - 5,4

2х = 14,4

х = 14,4 : 2

х = 7,2 — первое число

7,2 + 5,4 = 12,6 — второе число.

VI. Рефлексия

— Оцените свою работу на уроке.

Домашнее задание

С. 219, 1434, 1437 (а, б).