Решение задач на встречное движение - ПОВТОРЕНИЕ. РЕШЕНИЕ ЗАДАЧ

Основная дидактическая цель урока: учить решать задачи на встречное движение; повторить взаимосвязь между величинами “скорость”, “время”, “расстояние”; совершенствовать вычислительные навыки учащихся.

Ход урока

I. Организационный момент

II. Устный счет

1. Решите задачи.

1) Скорость катера 30 км/ч. Какой путь преодолеет катер за 3 ч?

2) За 4 ч пассажирский поезд прошел 240 км. Найдите скорость пассажирского поезда.

3) Пешеход прошел 20 км со скоростью 5 км/ч. Сколько времени он был в пути?

4) Скорость самолета 650 км/ч. Какое расстояние пролетит самолет за 4 ч?

2. Решите задачи по чертежам.

1)

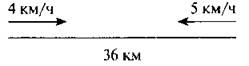
— Через какое время произойдет встреча?

2)

— Как найти скорость?

3)

— Как найти расстояние?

4)

— Какое расстояние будет между пешеходами через 2 ч?

III. Определение темы урока

— Исходя из устного счета, сформулируйте тему нашего урока.

IV. Решение задач

1. С. 268, № 1782.

— О каком движении идет речь в этой задаче?

— Что можем найти, зная расстояние и время, через которое произошла встреча?

— Что следует обозначить через х?

Пусть скорость грузовика будет х км/ч.

Тогда скорость легковой машины будет 2х км/ч.

Найдем скорость сближения: (х + 2х) км/ч.

Найдем скорость сближения иначе: (480 : 4) км/ч.

Оба выражения обозначают одно и то же.

Значит, можем составить уравнение:

х + 2х = 480 : 4

3х = 120

х = 120:3

х = 40 (км/ч) — скорость грузовика.

40 ∙ 2 = 80 (км/ч) — скорость легковой машины.

— К этой задаче можно составить и другое уравнение. Подумайте какое.

2. С. 268, № 1783 (работа в паре).

Проверка

Пусть скорость первого поезда будет х км/ч.

Тогда скорость второго поезда будет (х + 5) км/ч.

Скорость сближения равна (х + х + 5) км/ч.

Зная скорость сближения и время встречи, можем найти расстояние: (х + х + 5) ∙ 3.

А по условию расстояние равно 495 км.

Значит, можем составить уравнение:

(х + х + 5) ∙ 3 = 495

2х + 5 = 495 : 3

2х + 5 = 165

2х = 165 - 5

2х = 160

х = 160:2

х = 80 (км/ч) — скорость первого поезда.

80 + 5 = 85 (км/ч) — скорость второго поезда.

V. Решение комбинаторной задачи

На доске (слайде):

Сколько различных пятизначных чисел можно составить с помощью цифр 3; 4; 5; 6; 7, если цифры в записи числа не могут повторяться?

— Какие числа надо составить?

— Сколько цифр можем использовать?

— Какое стоит условие?

— Сколькими способами мы можем выбрать цифру на первое место? (5.)

— Сколькими способами можно выбрать вторую, третью, четвертую, пятую?

— Как решить эту задачу? (5! = 120 способов.)

VI. Самостоятельная работа

С. 261, № 1718 (4, 5) (работа в группе по 4 человека).

Проверка

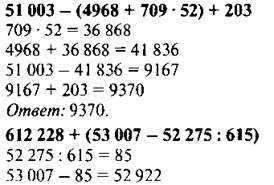
VII. Рефлексия

— Оцените свою работу на уроке.

Домашнее задание

С. 271, № 1815 (в, г); с. 273, № 1831.