Решение задач на движение вдогонку - ПОВТОРЕНИЕ. РЕШЕНИЕ ЗАДАЧ

Основная дидактическая цель урока: учить решать задачи на движение вдогонку; совершенствовать вычислительные навыки учащихся.

Ход урока

I. Организационный момент

II. Устный счет

1. С. 261, № 1717 (д, е, ж, з).

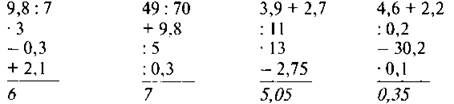
2. Решите задачи по чертежам.

— Догонит ли второй пешеход первого?

— Объясните почему.

— За счет чего второй пешеход будет догонять первого?

— Найдите разность скоростей.

— Как найти время?

— Решите задачу устно.

— Что нужно найти в задаче?

— Как найти расстояние?

— Какая скорость нам для этого нужна?

— Составьте план решения задачи.

— Решите задачу устно.

— Что нужно найти в задаче?

— Какую скорость мы можем узнать, зная расстояние и время, через которое первый велосипедист догонит второго?

— Что показывает разность скоростей?

— Решите задачу устно.

III. Определение темы урока

— Сформулируйте тему урока.

IV. Решение задач

1. С. 268, № 1780.

— У кого из мальчиков скорость больше? Почему?

— Какое расстояние было между мальчиками?

— Через сколько минут Паша догнал Борю?

— Что можем узнать, зная расстояние и время?

— Как теперь узнать скорость Паши?

— Сравните, в каких единицах даны скорость и расстояние.

— Что нужно сделать перед началом решения?

— Решите задачу.

0,2 км/мин = 200 м/мин

1) 360 : 9 = 40 (м/мин) — на столько скорость Паши больше.

2) 200 + 40 = 240 (м/мин) — скорость Паши.

2. С. 268, № 1782.

— Прочитайте задачу.

— Сравните ее с предыдущей.

— Какой путь решения выберем для этой задачи?

— Что обозначим через x?

— У кого из мальчиков скорость меньше?

Пусть скорость Коли будет x.

Тогда скорость Сережи будет 2х.

Разность скоростей мальчиков равна 2х — х.

Вычислим разность скоростей: 840 : 6.

Так как оба выражения обозначают одну и ту же величину, то можем составить уравнение:

1) 2х - x = 840 : 6

2) x = 140 (м/мин) — скорость Коли.

3) 140 ∙ 2 = 280 (м/мин) — скорость Сережи.

V. Геометрический материал

С. 266, № 1764 (устно).

VI. Решение комбинаторной задачи

На доске (слайде):

Сколько различных трехзначных чисел можно составить при помощи цифр 1; 3; 7; 4, если цифры в числе не могут повторяться и на месте десятков может быть только четное число?

— Прочитайте задачу.

— Что вы можете сказать про эту задачу?

— Какая цифра может стоять на месте десятков?

— Есть ли среди данных цифр такие, которые обозначают четное число? (Есть, это 4.)

— Сколькими способами можно выбрать первую цифру? (Тремя, четверку брать нельзя.)

— Сколькими способами можно выбрать вторую цифру? (На втором месте может стоять только четверка.)

— Сколькими способами можем выбрать третью цифру? (Двумя.)

— Как записать решение задачи? (3 ∙ 1 ∙ 2 = 6 чисел.)

— Запишите все возможные числа. (143; 341; 147; 741; 347; 743.)

VII. Самостоятельная работа

— Решите уравнения.

VIII. Рефлексия

— Какие задачи на движение для вас самые трудные? Почему?

Домашнее задание

С. 273, № 1830, 1834 (a).