Уравнение - Урок 2 - СЛОЖЕНИЕ И ВЫЧИТАНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ - НАТУРАЛЬНЫЕ ЧИСЛА

Основная дидактическая цель урока: учить решать усложненные уравнения; продолжить работу по обучению учащихся алгебраическому способу решения задач.

Ход урока

I. Организационный момент

II. Определение темы урока

— Разгадайте кроссворд.

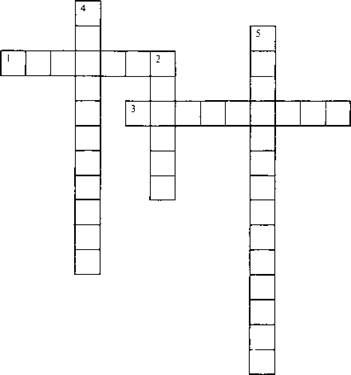
1) Часть прямой, ограниченная двумя точками. (Отрезок.)

2) Это есть у слова, растения и уравнения. (Корень.)

3) Равенство, содержащее неизвестное число, которое обозначено буквой. (Уравнение.)

4) Компонент действия вычитания, который находят сложением. (Уменьшаемое.)

5) Способ решения задач с помощью составления уравнений. (Алгебраический.)

— Попробуйте определить тему урока, опираясь на решенный кроссворд.

III. Устный счет

(Используются слайды презентации.)

1. Выполните задания.

— Назовите номера уравнений, в которых надо найти слагаемое.

— В каких уравнениях неизвестно уменьшаемое?

— В каких уравнениях надо найти вычитаемое?

— Найдите корни уравнений.

1) x + 17 = 60

2) а - 51 = 60

3) 60 = a + 51

4) с - 43 = 81

5) 62 = 100 - у

6) 59 + x = 59

7) 78 - a = 78

8) а + 45 = 45

9) x - 0 = 82

10) 70 - с = 68

— Что называется уравнением?

— Что такое корень уравнения?

2. Решите задачу.

Секретный замок состоит из двух барабанов, на каждом из которых можно выбрать цифру от 0 до 9. Сколькими способами можно выбрать шифр этого замка? (100.)

IV. Работа по теме урока

1. На слайде: 248 - (у + 123) = 24

— Назовите уменьшаемое в этом уравнении.

— Назовите вычитаемое.

— Что неизвестно?

— Подчеркните вычитаемое.

— Как найти вычитаемое?

248 - (у + 123) = 24

у + 123 = 248 - 24

у + 123 = 224

— Что теперь неизвестно?

— Как найти слагаемое?

у = 224 - 123

у = 101

Ответ: 101.

— Некоторые уравнения можно решить, опираясь на свойства сложения и вычитания. Рассмотрим второй способ решения этого уравнения.

248 – (у + 123) = 24

— Какое свойство можно применить при решении этого уравнения? (Сначала переместительное свойство сложения, а потом свойство вычитания суммы из числа.)

248 - (123 + у) = 24 — переместительное.

248 - 123 - у = 24 — вычитание суммы из числа.

125 - у = 24

у = 125 - 24

у = 101

Ответ: 101.

2. С. 61, № 375.

— Прочитайте объяснение.

Решим двумя способами данные уравнения.

(х + 98) + 14 = 169

x + 98 = 169 - 14

(x + 98) + 14 = 169

x + (98 + 14) = 169

Прибавление числа к сумме.

x + 98 = 155

x = 155 - 98

x = 57

x + 112 = 169

х = 169 – 112

х = 57

Ответ: 57.

(35 + у) - 15 = 31

35 + у = 31 + 15

(35 + у) - 15 = 31

(35 - 15) + у = 31

Вычитание числа из суммы.

35 + у = 46

у = 46 - 35

у = 11

20 + у = 31

у = 31 - 20

у = 11

Ответ: 11.

3. Выбрав любой способ, решите данные уравнения.

С. 61, № 376 (а, б, в).

(х + 15) - 8 = 17

x + (15 - 8) = 17

x + 7 = 17

x = 17 - 7

x = 10

Проверка

(10 + 15) - 8 = 17

25 – 8 = 17

17 = 17

Ответ: 10.

(24 + x) - 21 = 10

(24 - 21) + x = 10

3 + x = 10

x = 10 - 3

x = 7

Проверка

(24 + 7) - 21 = 10

31 - 21 = 10

10 = 10

Ответ: 7.

(45 - у) + 18 = 58

45 - y = 58 - 18

45 - y = 40

y = 45 - 40

y = 5

Проверка

(45 - 5) + 18 = 58

40 + 18 = 58

58 = 58

Ответ: 5.

V. Работа над задачами

1. С. 61, № 373 (в).

— Из чего складывается общее время? (Время движения + остановки.)

— Что нужно узнать в задаче?

— Какое правило надо помнить при решении задач способом составления уравнений?

— Что следует сделать до начала решения?

1 ч 15 мин = 75 мин

Пусть на остановки затрачено х мин.

Тогда время движения (75 - х) мин.

А по условию это равно 46 мин.

Значит, можем составить уравнение:

75 - х = 46

х = 75 - 46

х = 29 (мин) — затрачено на остановки.

Ответ: на остановки затрачено 29 мин.

2. С. 61, № 373 (г).

(Самостоятельная работа с последующей самопроверкой.)

Ответ: в поход ушли 47 человек.

VI. Повторение изученного материала

С. 63, № 383.

1. Прочитайте задание.

2. Начертите координатный луч и отметьте на нем данные точки.

3. Ответьте устно на вопросы.

VII. Решение комбинаторной задачи (исследование)

С. 63, № 388.

VIII. Решение выражений

1. С. 64. № 393 (а) (работа в паре с последующей проверкой).

(b + 179) - 89 = b + (179 - 89) = b + 90 при b = 56; 75.

Ответ: b + 90 = 56 + 90 = 146; b + 90 = 75 + 90 = 165.

2. С. 64. № 393 (б).

(839 + с) - 239 = (839 - 239) + с = 600 + с при с = 37; 98.

Ответ: 600 + с = 600 + 37 = 637; 600 + с = 600 + 98 = 698.

IX. Рефлексия

— Определите, что вам следует повторить дома по этой теме.

— Какое правило следует помнить при использовании алгебраического способа решения задач?

— На основе каких знаний можно решать уравнения?

Домашнее задание

С. 64, № 396 (а, б); с. 65, № 397 (в).