Поурочные разработки по Математике 5 класс к УМК Н.Я. Виленкина
Площадь - ПЛОЩАДИ И ОБЪЕМЫ - НАТУРАЛЬНЫЕ ЧИСЛА
Основная дидактическая цель урока: учить вычислять площади прямоугольников и квадратов, находить среди фигур равные; совершенствовать вычислительные навыки учащихся; продолжить работу с текстовыми задачами.
Ход урока
I. Организационный момент
II. Определение темы урока
— Разгадав математическую шараду, вы узнаете тему нашего урока.
Первую находим — вычисляем,
Много формул для нее мы знаем.
На второй же — митинги, парады,
Погулять по ней всегда мы рады.
— Сформулируйте тему урока.
III. Устная работа
На фигуры посмотри ты,
Дружок, внимательно.
Что сумеешь — вычисли.
Если сможешь - поспеши,
Равные средь них найди.
На доске:
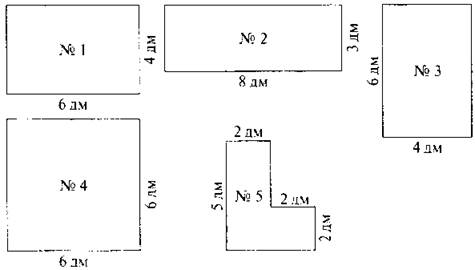
— Что же можно вычислить у этих фигур?
— По каким формулам можно вычислить периметр?
— Вычислите.
Р1 = 20 дм
Р2 = 22 дм
Р3 = 20 дм
Р4 = 24 дм
Р5 = 18 дм
— По каким формулам можно вычислить площадь?
— Составьте формулу для вычисления площади треугольника в фигуре № 4.
— Вычислите площади фигур.
S1 = 24 дм2
S2 = 24 дм2
S3 = 24 дм2
S4 = 36 дм2
Sтреуг = 18 дм2
S5 = 14 дм2
— Какие из фигур можно назвать равными? Почему?
— Почему не равны фигуры № 1 и 2?
— Сформулируйте свойства площадей.
IV. Работа по теме урока
1. С. 111, № 722.
— О скольких прямоугольниках идет речь?
— Что сказано про первый прямоугольник?
— Что известно про второй прямоугольник?
— Что надо найти в задаче?
Длина
Ширина
Площадь
16 см
← ?, на 12 см <
Равные
32 см
?
Равные
— Что нужно знать, чтобы найти ширину?
— Что сказано в задаче про площади?
— Можно ли найти площадь первого прямоугольника?
— Что для этого нужно знать?
— Можно ли вычислить ширину первого прямоугольника?
— Составьте план решения задачи.
— Решите задачу.
1) 16 — 12 = 4 (см) — ширина первого прямоугольника.
2) 16 ∙ 4 = 64 (см2) — площадь первого прямоугольника.
3) 64 : 32 = 2 (см) — ширина второго прямоугольника.
Sкв = а ∙ а
64 = а ∙ а
а = 8 (см) — квадрат с такой площадью имеет сторону 8 см.
2. С. 110, № 716 (устно).
3. С. 111, № 719, 720, 721 (устно).
V. Решение комбинаторной задачи
С. 112, № 733 (работа в паре).
Проверка
— Как записать решение? (5! = 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 120.)
— Придумайте похожую комбинаторную задачу.
(Учащиеся предлагают свои варианты задач, идет обсуждение.)
VI. Повторение изученного материала
(Самостоятельное решение задач после коллективного разбора с последующей самопроверкой.)
С. 112, № 734 (а, б, в).
(Эффективным является такой прием работы: записать условия всех трех задач, сравнить и сделать вывод о том, что все три задачи имеют одинаковый математический смысл. На примере первой задачи рассмотреть три способа решения и предложить учащимся (по вариантам) решить понравившимся способом.)
v
t
s
15 км/ч
8ч
? в 3 раза >
8ч
На ? больше
Норма
t
Всего
15 дет
8ч
? в 3 раза >
8ч
На ? больше
Масса 1 д.
Количество
Общая масса
15 г
8 дет.
? в 3 раза >
8 дет.
На ? больше
— Сравните условия задач. Что заметили?
Скорость — сколько пройдено за единицу времени.
Норма — сколько изготовлено за единицу времени.
Масса — какую массу имеет одна деталь.
Расстояние — сколько пройдено за 8 ч.
Всего — сколько изготовлено за 8 ч.
Общая масса — какую массу имеют 8 деталей.
— Каким действием находится каждая из трех величин?
— Что можно сказать про эти задачи?
Решение
1-й способ
1) 15 ∙ 3 = 45 (км/ч) — скорость мотоциклиста.
2) 45 ∙ 8 = 360 (км) — расстояние, пройденное мотоциклистом.
3) 15 ∙ 8= 120 (км) — расстояние, пройденное велосипедистом.
4) 360 — 120 = 240 (км) - на столько больше расстояние, пройденное мотоциклистом.
2-й способ
1) 15 ∙ 3 = 45 (км/ч) — скорость мотоциклиста.
2) 45 — 15 = 30 (км/ч) — на столько скорость мотоциклиста больше скорости велосипедиста.
3) 30 ∙ 8 = 240 (км) — на столько больше расстояние, пройденное мотоциклистом.
3-й способ
1) 15 ∙ 8= 120 (км) — расстояние, пройденное велосипедистом.
2) 120 ∙ 3 = 360 (км) — расстояние, пройденное мотоциклистом.
3) 360 — 120 = 240 (км) — на столько больше расстояние, пройденное мотоциклистом.
— Какой способ решения вам понравился больше?
— Решите задачи. Вариант 1 — б, вариант 2 — в.
VII. Рефлексия
— Как изменится площадь прямоугольника, если ширину увеличить в 2 раза? уменьшить в 3 раза?
— Как изменится площадь квадрата, если его сторону уменьшить в 2 раза?
Домашнее задание
С. 112, № 736, 740; с. 113, № 742.