Уравнения с модулями - Материалы для подготовки к самостоятельным работам

Пример 1. Решим уравнение:

а) |2x - 1| = 3;

б) |7x - 8| = -3;

в) |5x + 2| - 0.

Решение.

а) Модуль числа равен 3 лишь в двух случаях: если это число равно либо -3, либо 3: |2x - 1| = 3,

1) 2x - 1 = -3 или 2) 2x - 1 = 3.

Решив каждое из этих уравнений, получим, что корень уравнения 1) равен -1, а корень уравнения 2) равен 2. Следовательно, уравнение |2х - 1| = 3 имеет два корня: -1 и 2.

б) Так как ни при каком значении x модуль числа не равен отрицательному числу, то уравнение |7х - 8| = -3 не имеет корней.

в) Модуль числа равен 0 лишь в одном случае: если это число равно 0.

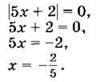
Ответ. а) -1; 2; б) нет корней; в)

Пример 2. Решим уравнение 8 - |5x - 7| = 1.

Решение. Прибавим к обеим частям уравнения число -8:

Умножим обе части уравнения на число -1: |5x - 7| = 7.

Модуль числа равен 7 лишь в двух случаях: если это число равно либо -7, либо 7:

1) 5х - 7 = -7 или 2) 5х - 7 = 7.

Решив каждое из этих уравнений, получим, что корень уравнения 1) равен 0, а корень уравнения 2) равен Следовательно, уравнение 8 - |5x - 7| = 1 имеет два корня:

Ответ.

Пример 3. Решим уравнение ||х - 12| - 2| = 5.

Решение. Модуль числа равен 5 лишь в двух случаях: если это число равно либо -5, либо 5:

Уравнение 1) не имеет корней, так как ни при каком значении х модуль числа не равен отрицательному числу.

Чтобы решить уравнение 2), надо найти корни каждого из уравнений:

3) х - 12 = 7 и 4) х - 12 = -7.

Решив каждое из этих уравнений, получим, что корень уравнения 3) равен 19, а корень уравнения 4) равен 5.

Ответ. 5; 19.

Пример 4. Решим уравнение |||2х + 5| + 2| - 5| = 6.

Решение. Заметим, что для любого значения х число |2х + 5| + 2 положительно, поэтому данное уравнение можно переписать в виде ||2х + 5| - 3| = 6.

Модуль числа равен 6 лишь в двух случаях: если это число равно либо -6, либо 6:

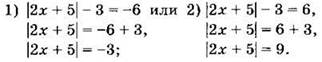
Уравнение 1) не имеет корня, так как ни при каком значении х модуль числа не равен отрицательному числу.

Чтобы решить уравнение 2), надо найти корни каждого из уравнений:

3) 2х + 5 = -9 и 4) 2х + 5 = 9.

Решив каждое из этих уравнений, получим, что корень уравнения 3) равен -7, а корень уравнения 4) равен 2. Следовательно, уравнение |2х + 5| - 3 = 6 имеет два корня: -7 и 2. Значит, и уравнение |||2x + 5| + 2| - 5| = 6 имеет два корня: -7 и 2.

Ответ. -7; 2.