Самостоятельные и контрольные работы по алгебре 7 класс - К учебнику Ю. Н. Макарычева Алгебра. 7 класс - 2015
Умножение многочлена на многочлен. Разложение многочленов на множители методом группировки - КОНТРОЛЬНЫЕ РАБОТЫ
Вариант 1
А1. Представьте в виде суммы произведение

А2. Преобразуйте в многочлен стандартного вида
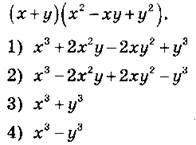
А3. Разложите на множители 3а – 4b + 6ах – 8bх.
![]()
В1. Разложите на множители ![]()
С1. Разложите на множители квадратный трехчлен х2 – 6x + 8.
С2. Решите задачу.
Четыре последовательных натуральных числа таковы, что произведение двух больших из этих чисел на 90 больше, чем произведение двух меньших чисел. Найдите меньшее из этих чисел.
Вариант 2
А1. Представьте в виде суммы произведение

А2. Преобразуйте в многочлен стандартного вида
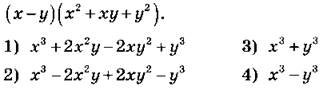
А3. Разложите на множители 4a - 3b + 12ax - 9bx.
![]()
В1. Разложите на множители ![]()
С1. Разложите на множители квадратный трехчлен х2 + 6х + 8.
С2. Решите задачу.
Четыре последовательных натуральных числа таковы, что произведение двух меньших из этих чисел на 78 меньше, чем произведение двух больших чисел. Найдите меньшее из этих чисел.
Вариант 3
А1. Представьте в виде суммы произведение
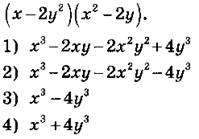
А2. Преобразуйте в многочлен стандартного вида
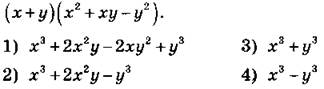
А3. Разложите на множители 5a - 6b + 10ay - 12by.
![]()
В1. Разложите на множители ![]()
С1. Разложите на множители квадратный трехчлен х2 - 5х + 6.
С2. Решите задачу.
Если одну из сторон квадрата увеличить на 5, а смежную с ней уменьшить на 3, то площадь полученного прямоугольника будет на 29 больше площади квадрата. Найдите сторону квадрата.
Вариант 4
А1. Представьте в виде суммы произведение
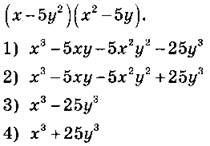
А2. Преобразуйте в многочлен стандартного вида
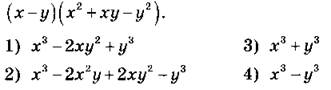
А3. Разложите на множители 6a - 5b + 18ay - 15by.
![]()
В1. Разложите на множители ![]()
С1. Разложите на множители квадратный трехчлен x2 + 5x + 6.
С2. Решите задачу.
Если одну сторону квадрата уменьшить на 4, а смежную с ней увеличить на 6, то площадь полученного прямоугольника будет на 32 больше площади квадрата. Найдите сторону квадрата.