Контрольная работа № 3 по теме Функции - ЛИНЕЙНАЯ ФУНКЦИЯ - ФУНКЦИИ

Цель: проверить знания, умения и навыки учащихся по теме.

Тип урока: урок контроля, оценки и коррекции знаний.

Ход урока

I. Сообщение темы и цели урока

II. Общая характеристика контрольной работы

Контрольная работа составлена в шести вариантах (варианты 1,2 — самые простые, варианты 3, 4 — средней сложности, варианты 5, 6 — самые сложные). Степень сложности меняется не слишком резко, поэтому можно рекомендовать следующий критерий оценки: при выполнении вариантов 1, 2 оценка “3” ставится за любые три решенные задачи, оценка “4” — за четыре задачи и оценка “5” — за пять задач. Одна задача дает учащимся некоторую свободу выбора. При тех же критериях оценки за решение задач вариантов 3, 4 к набранным баллам добавляются дополнительно 0,5 балла, за решение задач вариантов 5,6 — дополнительно 1 балл (т. е. оценка “5” ставится уже за четыре задачи). Все задачи в варианте примерно равноценны. Возможно, несколько труднее для учеников задачи 5, 6.

Перед проведением контрольной работы учащихся целесообразно ознакомить с критериями оценки и разной сложностью вариантов. Выбор вариантов может быть осуществлен учителем или предоставлен ученикам (в этом случае предполагается наличие копировальной техники в школе и избыточное количество заданий). При наличии такой техники в классе на стенде (после контрольной) может быть вывешено решение всех задач шести вариантов.

Контрольная работа рассчитана на один урок.

III. Контрольная работа

Вариант 1

1. Функция задана формулой у = 2х + 3. Принадлежат ли графику функции точки А (1; 5) и В (-1; -1)?

2. Постройте график функции у = -4х + 3 и укажите координаты точек пересечения графика с осями координат.

3. Постройте график зависимости у = kх, если он проходит через точку А (-2; 4). Найдите угловой коэффициент k.

4. При каком значении параметра а графики функций у = 3х – 2 и у = 7 + (а - 2) ∙ х параллельны?

5. Найдите точку пересечения графиков функций у = 3 и у = 2х - 1.

6. Постройте график зависимости |у + 1| = 2.

Вариант 2

1. Функция задана формулой у = -2х + 5. Принадлежат ли графику функции точки А (1; 3) и В (-1; 6)?

2. Постройте график функции у = 3х + 4 и укажите координаты точек пересечения графика с осями координат.

3. Постройте график зависимости у = kх, если он проходит через точку А (2; -6). Найдите угловой коэффициент k.

4. При каком значении параметра а графики функций у = 5х + 3 и у = -4 + (а + 3) ∙ х параллельны?

5. Найдите точку пересечения графиков функций у = -1 и у = 3х + 2.

6. Постройте график зависимости |у - 2| = 1.

Вариант 3

1. Функция задана формулой у = 2х² + |х| + 1. Принадлежат ли графику функции точки А (1; 4) и В (-1; 5)? Найдите точку пересечения графика с осью ординат.

2. Постройте график функции у = |x| - 1 и укажите координаты точек пересечения графика с осями координат.

3. Постройте график функции

4. При каком значении параметра а графики функций у = 6х – 3 и у = (4а + 2)х - 2а - 1 параллельны?

5. Найдите точку пересечения графиков функций у = -2х и у = 2х - 4. Постройте эти графики.

6. Постройте график зависимости |у + 2х| = 3.

Вариант 4

1. Функция задана формулой у = 2|х| - х² + 3. Принадлежат ли графику функции точки А (1; 4) и В (-1; 3)? Найдите точку пересечения графика с осью ординат.

2. Постройте график функции у = 1 - |х| и укажите координаты точек пересечения графика с осями координат.

3. Постройте график функции

4. При каком значении параметра а графики функций у = 4х + 5 и у = 1 - 2а - (3а + 2) ∙ х параллельны?

5. Найдите точку пересечения графиков функций у = 2х и у = 6 - х. Постройте эти графики.

6. Постройте график зависимости |у - 3х| = 2.

Вариант 5

1. График линейной функции у = kх + b проходит через точки А (0; -3) и В (2; 0). Постройте график функции и определите функцию (найдите k и b).

2. Укажите координаты точек пересечения графика функции у = 2х² + 3х с осями координат.

3. Найдите координаты точки графика функции у = 3х - 7, если эти координаты равны. Постройте график и укажите найденную точку.

4. Постройте график зависимости |у - 2х + 1| = 2.

5. Найдите точку пересечения графиков функций у = 7х - 31 и у = 2х - 6.

6. Постройте график зависимости |х + 1| + |х - 1| = 2.

Вариант 6

1. График линейной функции у = kх + b проходит через точки A (0; 2) и В (-3; 0). Постройте график функции и определите функцию (найдите k и b).

2. Укажите координаты точек пересечения графика функции у = 3х² + 2х с осями координат.

3. Найдите координаты точки графика функции у = -3х + 5, если эти координаты равны. Постройте график и укажите найденную точку.

4. Постройте график зависимости |у + 2х - 2| = 1.

5. Найдите точку пересечения графиков функций у = 9х - 43 и у = 3х - 7.

6. Постройте график зависимости |у - 1| + |у + 1| = 2.

IV. Подведение итогов контрольной работы

1. Распределение работ по вариантам и результаты решения. Удобно данные заносить в таблицу (для каждой пары вариантов).

№ задачи	Итоги
	+	±	-	Ø
1	5	1	1	1
2
...
6

Обозначения:

+ — число решивших задачу правильно или почти правильно;

± — число решивших задачу со значительными погрешностями;

- — число не решивших задачу;

Ø — число не решавших задачу.

Варианты 1, 2 — 8 учащихся.

2. Типичные ошибки при решении задач.

3. Задачи, вызвавшие наибольшие трудности.

V. Разбор задач (ответы и решения)

Вариант 1

1. Точка А принадлежит, В — не принадлежит.

2. А (0; 3) и B (3/4; 0).

3. k = -2.

4. а = 5.

5. A (2; 3).

6. Прямые у = 1 и у = -3.

Вариант 2

1. Точка А принадлежит, В — не принадлежит.

2. A (0; 4) и B (-4/3; 0).

3. k = -3.

4. а = 2.

5. A (-1; -1).

6. Прямые у = 1 и у = 3.

Вариант 3

1. Точка А принадлежит, В — не принадлежит, С (0; 1).

2. А (0; -1), В (-1; 0), С (1; 0).

3. Прямая у = 4 - 2х, где x ≠ 1.

4. Таких значений а нет.

5. А (1; -2).

6. Прямые у = -2х + 3 и у = -2х - 3.

Вариант 4

1. Точка А принадлежит, В — не принадлежит, С (0; 3).

2. A (0; 1), B (-1; 0), С (1; 0).

3. Прямая у = 2х + 4, где х ≠ -1.

4. Таких значений а нет.

5. А (2; 4).

6. Прямые у = 3х + 2 и у = 3х - 2.

Вариант 5

1. Дано: А (0; -3) и В (2; 0) — точки пересечения графика линейной функции у = kх + b с осями координат. Построим эти точки и проведем через них прямую.

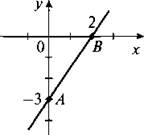
Так как прямая проходит через точку А, то подставим ее координаты в функцию и получим -3 = k ∙ 0 + b, откуда b = -3. Тогда функция имеет вид у = kх - 3. Подставим координаты точки В в функцию 0 = k ∙ 2 - 3, откуда k = 2/3 = 1,5. Значит, функция имеет вид у = 1,5х - 3.

(Ответ: у = 1,5х - 3.)

2. Найдем координаты точек пересечения графика функции у = 2х² + 3х с осями координат. Для нахождения точек пересечения с осью абсцисс положим у = 0 и получим уравнение 0 = 2х² + 3х. Используя распределительное свойство, запишем уравнение в виде 0 = х(2х + 3). Так как произведение множителей равно нулю, то один из них равен нулю. Получаем х = 0 и 2х + 3 = 0 (откуда х = -3/2). Итак, имеем точки пересечения с осью абсцисс А (0; 0) и В (-3/2; 0). Так как точка А — начало координат, то она одновременно является и точкой пересечения графика функции с осью ординат.

(Ответ: А (0; 0), B (-3/2; 0).)

3. На графике функции у = 3х - 7 есть точка А, координаты которой равны, т. е. х = а и у = a. Эти координаты должны удовлетворять уравнению функции. Подставив их, получаем а = 3а - 7, откуда а = 3,5. Итак, имеем точку А (3,5; 3,5). Построим график функции у = 3х - 7 и отметим на нем точку А.

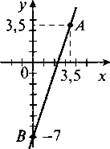
(Ответ: А (3,5; 3,5).)

4. Построим график зависимости |у - 2х + 1| = 2.

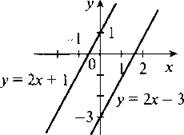
Если модуль некоторой величины равен 2, то сама величина может равняться 2 или -2. Рассмотрим эти случаи.

Если у - 2х + 1 = 2, то у = 2х + 1;

если у - 2х + 1 = -2, то у = 2х - 3.

Построим две параллельные прямые у = 2х + 1 и у = 2х - 3, которые являются графиком данной зависимости.

5. Пусть A (х₀; у₀) — точка пересечения графиков функций у = 7х - 31 и у = 2х - 6. Так как точка А принадлежит графику каждой функции, то и ее координаты удовлетворяют каждой функции, т. е. выполняются равенства у₀ = 7 ∙ х₀ - 31 и у₀ = 2 ∙ х₀ - 6. В этих равенствах одинаковые левые части, поэтому приравняем правые части. Получаем уравнение 7 ∙ х₀ - 31 = 2 ∙ х₀ - 6 для нахождения абсциссы точки пересечения. Запишем уравнение в виде 7 ∙ х₀ - 2 ∙ х₀ = 31 - 6 или 5 ∙ х₀ = 25 и найдем х₀ = 5. Теперь из любого уравнения, например из первого, определяем y₀ = 7 ∙ x₀ - 31 = 7 ∙ 5 – 31 = 4. Итак, координаты точки А (5; 4).

(Ответ: А (5; 4).)

6. При построении графика зависимости |х + 1| + |х - 1| = 2 учтем геометрический смысл модуля. Величина |х + 1| = |х - (-1)| — расстояние от точки х до точки -1 на координатной оси, величина |х - 1| — расстояние от точки х до точки 1.

Тогда геометрический смысл выражения |х + 1| + |х - 1| — сумма расстояний от точки х до точек -1 и 1. На рисунке видно, что сумма таких расстояний будет равна 2, если точка х располагается между точками -1 и 1 на координатной оси, т. е. -1 ≤ х ≤ 1. Теперь на координатной плоскости построим множество таких точек.

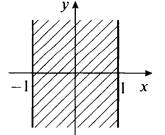
Сначала строим две параллельные прямые х = -1 и х = 1 (границы области). При этом координата у может быть любой. Тогда условию -1 ≤ х ≤ 1 удовлетворяют все точки плоскости, расположенные между построенными прямыми х = -1 и х = 1 и на них (эти точки заштрихованы).

Вариант 6

1. Дано: А (0; 2) и В (-3; 0) — точки пересечения графика линейной функции у = kх + b с осями координат. Построим эти точки и проведем через них прямую.

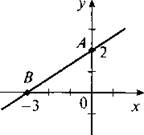
Так как прямая проходит через точку А, то подставим ее координаты в функцию и получим 2 = k ∙ 0 + b, откуда b = 2. Тогда функция имеет вид у = kх + 2. Подставим координаты точки В в эту функцию: 0 = k ∙ (-3) + 2, откуда k = 2/3. Значит, функция имеет вид у = 2/3х + 2.

(Ответ: у = 2/3х + 2.)

2. Найдем координаты точек пересечения графика функции у = 3х² + 2х с осями координат. Для нахождения точек пересечения с осью абсцисс положим у = 0 и получим уравнение 0 = 3х² + 2х. Используя распределительное свойство, запишем уравнение в виде 0 = х(3х + 2). Так как произведение множителей равно нулю, то один из них равен нулю. Получаем х = 0 и 3х + 2 = 0 (откуда х = -2/3). Итак, точки пересечения с осью абсцисс А (0; 0) и В (-2/3; 0). Так как точка А — начало координат, то она одновременно является и точкой пересечения графика функции с осью ординат.

(Ответ: А (0; 0) и B (-2/3; 0).)

3. На графике функции у = -3х + 5 есть точка А, координаты которой равны, т. е. х = а и у = а. Эти координаты удовлетворяют уравнению функции. Подставим их, получаем а = -3а + 5, откуда а = 5/4. Итак, имеем точку А (5/4; 5/4). Построим график функции у = -3х - 5 и отметим на нем точку А.

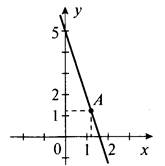
(Ответ: А (5/4; 5/4).)

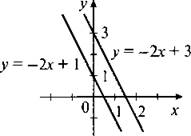
4. Построим график зависимости |у + 2х - 2| = 1. Если модуль некоторой величины равен 1, то сама величина может равняться 1 или -1. Рассмотрим эти случаи.

Если у + 2х - 2 = 1, то у = -2х + 3;

если у + 2х - 2 = -1,тоу = -2х + 1.

Построим две параллельные прямые у = -2х + 3 и у = -2х + 1, которые являются графиком данной зависимости.

5. Пусть А (x₀; у₀) — точка пересечения графиков функций у = 9х - 43 и у = 3х - 7. Так как точка А принадлежит графику каждой функции, то и ее координаты удовлетворяют каждой функции, т. е. выполняются равенства у₀ = 9 ∙ х₀ - 43 и у₀ = 3 ∙ х₀ - 7. В этих равенствах одинаковые левые части, поэтому приравняем правые части. Получаем уравнение 9 ∙ х₀ - 43 = 3 ∙ х₀ - 7 для нахождения абсциссы точки пересечения. Запишем уравнение в виде 9 ∙ х₀ = 3 ∙ х₀ = 43 - 7 или 6 ∙ х₀ = 36 и найдем х₀ = 6. Теперь из любого уравнения, например из первого, определяем у₀= 9 ∙ х₀ - 43 = 9 ∙ 6 - 43 = 11. Итак, координаты точки А (6; 11).

(Ответ: А (6; 11).)

6. При построении графика зависимости |у - 1| + |у + 1| = 2 учтем геометрический смысл модуля. Величина |у - 1| — расстояние от точки у до точки 1 на координатной оси, величина |у + 1| = |у - (-1)| — расстояние от точки у до точки -1.

Тогда геометрический смысл выражения |у - 1| + |у + 1| — суммарное расстояние от точки у до точек 1 и -1.

На рисунке видно, что сумма таких расстояний будет равна 2, если точка у располагается между точками -1 и 1 на координатной оси, т. е. -1 ≤ у ≤ 1. Теперь на координатной плоскости построим множество таких точек.

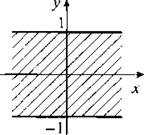
Сначала строим две параллельные прямые у = -1 и у = 1 (границы области). При этом координата х может быть любой. Тогда условию -1 ≤ у ≤ 1 удовлетворяют все точки плоскости, расположенные между построенными прямыми у = -1 и у = 1 и на них (эти точки заштрихованы).

VI. Подведение итогов урока