Определение степени с натуральным показателем - СТЕПЕНЬ И ЕЕ СВОЙСТВА - СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ

Цель: развить навыки возведения в степень.

Планируемые результаты: освоить понятие степени с натуральным показателем.

Тип урока: урок изучения нового материала.

Ход урока

I. Сообщение темы и цели урока

II. Работа по теме урока

Степенью числа а с натуральным показателем п называется произведение п одинаковых сомножителей а и обозначается символом аⁿ (n ≥ 2), т. е. Если степень равна единице (т. е. n= 1), то а¹ равняется числу а (т. е. а¹ = а). Повторяющийся множитель а называется основанием степени, число повторяющихся множителей n — показателем степени. Степень аⁿ с основанием а и показателем n читается так: “а в степени n” или “n-я степень числа а”. Нахождение значения степени называют возведением в степень.

Пример 1

а) (3 в шестой степени, или шестая степень числа 3);

б) (0 во второй степени, или 0 в квадрате, или вторая степень числа 0);

в) (-2 в четвертой степени, или четвертая степень числа (-2));

г) в третьей степени, или (-1/3) в кубе, или третья степень числа (-1/3));

д) При этом десятичная дробь 0,(6) была обращена в обыкновенную дробь 2/3.

Аналогично можно использовать определение степени числа и в алгебраических выражениях.

Пример 2

(очевидно, что b ≠ 0);

В натуральную степень можно возводить любые числа: отрицательные, нуль, положительные. При возведении в степень положительного числа получается положительное число. При возведении в степень нуля получается нуль. При возведении в степень отрицательного числа может получиться как отрицательное, так и положительное число. При этом если показатель степени — четное число, то при возведении получается положительное число. Если показатель степени — нечетное число, то при возведении получается отрицательное число (см. пример 1).

Действительно, если n — четное число, то произведение четного числа отрицательных множителей положительно. Если n — нечетное число, то произведение нечетного числа отрицательных множителей отрицательно.

Знак степени аⁿ

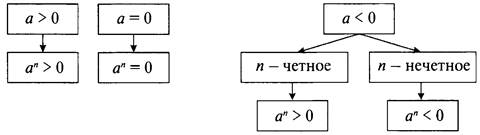
Из приведенной схемы следует, что при четном показателе n степень числа аⁿ ≥ 0 при любом значении а.

Пример 3

При любых значениях переменных а и b выражения а², а⁶, (а - b)², (2а + 3b)⁴ и т. д. принимают только неотрицательные значения.

Понятие степени числа с натуральным показателем позволяет решать более сложные задачи.

Пример 4

Найдем значения выражений:

(здесь учтено, что

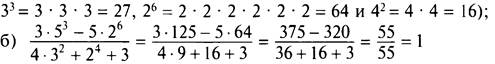(здесь учтено, что ).

III. Задания на уроке

№ 374 (а, в, ж, и), 375 (б, г), 376, 381 (а), 385 (а, г, д), 388 (д, з), 392 (а), 395 (б, г), 397.

IV. Контрольные вопросы

— Дайте определение степени с натуральным показателем.

— Дайте определение основания степени.

— Дайте определение показателя степени.

— Какое число получается при возведении положительного числа в степень?

— Какое число получается при возведении нуля в степень?

— Какое число получается при возведении отрицательного числа в степень? От чего зависит результат?

V. Подведение итогов урока

Домашнее задание

№ 374 (б, д, е, з), 375 (а, д), 377, 381 (б), 385 (б, в, е), 388 (е, и), 392 (б), 395 (а, в), 398.