Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Умножение разности двух выражений на их сумму - РАЗНОСТЬ КВАДРАТОВ. СУММА И РАЗНОСТЬ КУБОВ - ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
Цель: ознакомить с формулой для нахождения разности квадратов и ее применением.
Планируемые результаты: освоить умножение разности двух выражений на их сумму.
Тип уроков: урок-исследование, урок-практикум.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Преобразуйте в квадрат двучлена трехчлен:
![]()
2. Докажите неравенство ![]()
Вариант 2
1. Преобразуйте в квадрат двучлена трехчлен:
![]()
2. Докажите неравенство ![]()
III. Работа по теме урока
Приведем еще одну формулу сокращенного умножения:
![]()
которая позволяет быстро умножать разность и сумму одних и тех же чисел а и b.
Выведем эту формулу.
Алгебраический способ
Умножим разность чисел а - b на их сумму а + b. Получаем ![]()
Геометрический способ
Рассмотрим фигуру, изображенную на рисунке.
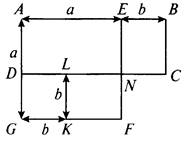
Стороны прямоугольника ABCD равны: АВ = а + b и AD = а - b (для определенности считаем, что а, b > 0 и а > b), и его площадь S = AD ∙ АВ = (а - b)(а + b). Этот прямоугольник состоит из прямоугольников AEND и EBCN. Прямоугольник EBCN равен прямоугольнику KLNF. Поэтому площадь S равна площади фигуры AENFKLD, которая равна разности площадей квадратов AEFG (со стороной а) и DLKG (со стороной b), т. е. S = а2 - b2. Приравняв два выражения для площади S, получаем равенство ![]()
В соответствии с тождеством (1) произведение разности чисел (выражений) и их суммы равно разности квадратов этих чисел (выражений). Тождество (1) широко используется при алгебраических преобразованиях выражений.
Пример 1
Перемножим числа 47 и 53, записав их в виде разности и суммы двух чисел: 47 = 50 - 3 и 53 = 50 + 3. Используя формулу (1), получаем ![]()
Пример 2
Сравним числа ![]()
Получаем ![]()
![]()
Тогда число А имеет следующий вид: ![]()
![]()
Изменим порядок умножения сомножителей, перемножив сначала два крайних числа, а затем два средних. Получаем ![]()
Используя формулу (1), имеем ![]()
Очевидно, что в таком произведении каждый множитель меньше числа 1462, т. е. 1462 - 52 < 1462 и 1462 - 22 < 1462. Поэтому произведение меньше ![]() Таким образом, число А меньше числа В, т. е. А < В.
Таким образом, число А меньше числа В, т. е. А < В.
Пример 3
Перемножим выражения 4а – 5b и 4а + 5b.
Используя формулу (1) и правила действий со степенями, получаем ![]()
Пример 4
Представим в виде многочлена выражение (3а3 – 2b2)(3а3 + 2b2).
Используя формулу (1), получаем ![]()
![]()
Пример 5
Перемножим выражения -6а – 5b и 6а – 5b.
В первом выражении -6а – 5b вынесем за скобки число (-1) и получим ![]()
![]()
Заметим, что преобразование можно выполнить и сразу: ![]()
Пример 6
Упростим выражение ![]()
![]()
Раскроем скобки, а для первого произведения используем формулу (1). Получаем
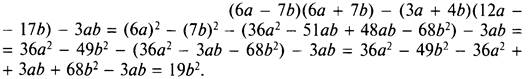
IV. Задания на уроках
№ 854 (в, д), 855 (б, г), 857 (г), 858 (а), 859 (в, г), 861 (а, г, ж), 862 (в), 867 (б), 869 (а, д), 873 (а, д).
V. Контрольные вопросы
— Сформулируйте словами, как найти произведение разности и суммы двух выражений, и запишите соответствующую формулу.
— Выведите формулу произведения разности и суммы двух выражений алгебраическим способом.
— Выведите формулу произведения разности и суммы двух выражений геометрическим способом.
VI. Творческие задания
1. Выполните действия:
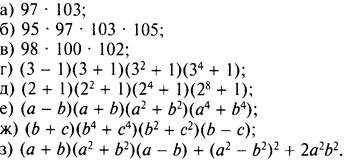
Ответы: а) 9991; б) 99 660 025; в) 999 600; г) 38 - 1; д) 216 - 1 (умножить выражение на 2 - 1 = 1); е) а8 – b8; ж) b8 - с8 (изменить порядок умножения); з) 2а4.)
2. Сравните числа:

(Ответ: первые числа меньше, чем вторые.)
VII. Подведение итогов уроков
Домашнее задание
№ 854 (б, е), 855 (в, д), 857 (д), 858 (б), 859 (ж, з), 861 (б, д, з), 862 (г), 867 (д), 869 (б, е), 873 (б, е).