Выражения с переменными - ВЫРАЖЕНИЯ - ВЫРАЖЕНИЯ, ТОЖДЕСТВА, УРАВНЕНИЯ

Цель: ознакомить с понятиями алгебраического выражения и его значения.

Планируемые результаты: усвоить понятия алгебраического выражения и его значения при заданных значениях переменных.

Тип урока: урок общеметодологической направленности.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Выполните действия:

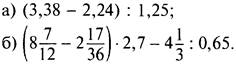
2. В сплаве цинка и свинца массой 1600 г содержится 25% свинца. Установите:

а) массу цинка и массу свинца в сплаве (в граммах);

б) сколько процентов цинка в сплаве;

в) какой процент составляет масса свинца от массы цинка.

Вариант 2

1. Выполните действия:

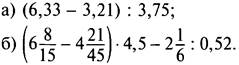
2. В сплаве меди и олова массой 1400 г содержится 30% олова. Установите:

а) массу меди и массу олова в сплаве (в граммах);

б) сколько процентов меди в сплаве;

в) какой процент составляет масса олова от массы меди.

III. Работа по теме урока

План урока

1. Выражение с переменными.

2. Значение выражения с переменными.

1. Выражение с переменными

Сначала рассмотрим несколько примеров.

Пример 1

Один диск стоит 230 руб. Тогда два таких диска стоят в два раза больше, т. е. 230 ∙ 2 = 460 руб.; пять дисков стоят в пять раз больше, т. е. 230 ∙ 5 = 1150 руб.; а дисков стоят в а раз дороже, т. е. 230 ∙ а руб. С помощью выражения 230 ∙ а можно находить стоимость различного числа дисков, подставляя различные значения а и выполняя умножение.

Так как буква а может принимать различные натуральные значения, то ее называют переменной, а выражение 230 ∙ а — выражением с переменной (или алгебраическим выражением).

Пример 2

Пусть длина одной стороны прямоугольника а см, другой стороны — b см. Найдем периметр прямоугольника.

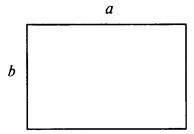
Так как противоположные стороны прямоугольника равны, то длина двух меньших сторон 2 ∙ а см, длина двух больших сторон 2 ∙ b см.

Тогда периметр (сумма длин всех сторон) прямоугольника равен 2 ∙ а + 2 ∙ b (см). Используя алгебраическое выражение 2 ∙ а + 2 ∙ b, можно находить периметр прямоугольника со сторонами а см и b см. Буквы а и b могут принимать различные положительные значения и называются переменными.

Пример 3

Поезд двигался 2 ч со скоростью v₁ км/ч и 3 ч со скоростью v₂ км/ч. Найдем среднюю скорость движения поезда.

По определению средняя скорость движения — отношение всего пройденного пути ко времени, затраченного на этот путь. За первые два часа поезд, двигаясь со скоростью км/ч, прошел расстояние 2 ∙ v₁ (км). За следующие три часа поезд, двигаясь со скоростью v₂ км/ч, прошел расстояние 3 ∙ v₂ (км).

Таким образом, было пройдено расстояние 2 ∙ v₁ + 3 ∙ v₂ (км), на которое было затрачено 2 + 3 = 5 (ч). Тогда по определению средняя скорость поезда равна

Вновь получили алгебраическое выражение с переменными и v₁ и v₂.

Таким образом, в различных алгебраических, геометрических и физических задачах появляются выражения с переменными (или алгебраические выражения). Возникновение таких выражений подобно возникновению числовых выражений. Поэтому многие понятия у числовых и алгебраических выражений аналогичны.

Запись, составленная из букв и чисел с помощью арифметических действий и скобок, называется алгебраическим выражением. Буквы, входящие в выражение, называются переменными.

Пример 4

а) Запись — алгебраическое выражение с переменными а и b;

б) запись — алгебраическое выражение с переменными x и у.

2. Значение выражения с переменными

Значение числового выражения, которое получается при подстановке выбранных значений переменных в алгебраическое выражение, называют значением алгебраического выражения (выражения с переменными).

Пример 5

Найдем значение выражения при a = 3, b = 4 и с = 2. В указанное алгебраическое выражение подставим данные значения переменных а = 3, b = 4 и с = 2. Получаем числовое выражение. Выполнив действия, найдем его значение: Это число является значением алгебраического выражения для данных значений переменных.

IV. Задания на уроке

№ 31, 33, 35, 36, 38 (а, б, г), 20, 22, 26 (а).

V. Контрольные вопросы

— Чем различаются числовые и алгебраические выражения?

— Что называется алгебраическим выражением и переменной?

— Как вычислить значение алгебраического выражения при данных значениях переменных? Всегда ли это можно сделать?

VI. Творческие задания

1. Первое положительное число увеличили на 10%, второе положительное число — на 50%. Может ли сумма этих чисел увеличиться на 30%?

Решение

Пусть первое число л, второе — у. Сумма этих чисел х + у. После увеличения

первое число равно:

второе число равно:

Тогда сумма этих чисел равна 1,1 ∙ х + 1,5 ∙ у. По условию эта величина равна первоначальной сумме, увеличенной на 30%, т. е.:

Получаем равенство:

откуда x = y.

Таким образом, условия задачи выполнены, если первоначальные числа равны.

2. Докажите на примере трехзначного числа признаки делимости на 2, 3, 4, 5, 9.

Решение

Пусть трехзначное число состоит из а сотен, b десятков и с единиц. Тогда его можно записать в виде 100 ∙ а + 10 ∙ b + с. Теперь рассмотрим делимость этого числа на перечисленные числа 2, 3, 4, 5, 9.

а) Число делится на 2, если его последняя цифра четная или 0. В данном числе 100 ∙ а + 10 ∙ b + с первые два слагаемых 100 ∙ а и 10 ∙ b при всех а и b делятся на 2. Поэтому, чтобы данное число делилось на 2, надо, чтобы и последнее слагаемое с делилось на 2. Таким образом, последняя цифра данного числа четная или нуль.

б) Число делится на 3 (9), если сумма его цифр делится на 3 (9). В данном числе 100 ∙ а + 10 ∙ b + с выделим слагаемые, которые делятся на 3 (9), т. е. запишем число в виде (99 ∙ а + 9 ∙ b) + (а + b + с). Каждое слагаемое в первых скобках делится на 3 (9). Чтобы данное число делилось на 3 (9), надо, чтобы и последнее слагаемое а + b + с делилось на 3 (9). Смысл этого слагаемого — сумма цифр данного числа.

в) Число делится на 4, если двузначное число 10 ∙ b + с, образованное двумя последними цифрами, делится на 4. В данном числе 100 ∙ a + 10 ∙ b + с первое слагаемое 100 ∙ а делится на 4. Чтобы число делилось на 4, надо, чтобы и выражение 10 ∙ b + с делилось на 4. Смысл выражения 10 ∙ b + с — двузначное число, образованное двумя последними цифрами данного числа.

г) Число делится на 5, если его последняя цифра 0 или 5. В данном числе 100 ∙ а + 10 ∙ b + с первые два слагаемых делятся на 5 при любых а и b. Поэтому необходимо, чтобы и число с делилось на 5.

Так как с — последняя цифра числа, то с может принимать значения или 0, или 5.

3. При каком значении цифры X шестизначное число 3Х54ХХ делится на 2, 3, 4, 5, 9?

4. При каком значении цифр X и Y шестизначное число 2X541 Y делится на 12, 15, 18, 20?

(Указание: разложить делители на взаимно простые множители: 12 = 3 ∙ 4; 15 = 3 ∙ 5; 18 = 2 ∙ 9; 20 = 4 ∙ 5 — и использовать соответствующие признаки делимости.)

VII. Подведение итогов урока

Домашнее задание

№ 32, 34, 37, 38 (в, д, е, ж, з), 21, 23, 26 (в).