Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Способ сложения - РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ - СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Цель: рассмотреть способ сложения для решения систем линейных уравнений.
Планируемые результаты: научиться применять способ сложения для решения систем линейных уравнений.
Тип уроков: урок изучения нового материала, урок-практикум.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
Способом подстановки решите систему уравнений:
![]()
Вариант 2
Способом подстановки решите систему уравнений:
![]()
III. Работа по теме урока
Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При таком способе решения данная система уравнений заменяется равносильной системой, в которой одно из уравнений содержит только одну переменную.
Пример 1
Решим систему уравнений
![]()
Заметим, что в уравнениях системы коэффициенты при переменной у являются противоположными числами. Сложим почленно правые и левые части уравнений: 3х + 2у + 4х - 2у = 8 + 6. Получим линейное уравнение с одной переменной х, а именно 7х = 14. Заменим одно из уравнений системы (1), например первое, полученным уравнением 7х = 14.
Получим равносильную систему
![]()
Решим систему (2). Из первого уравнения находим x = 2. Подставим это значение x во второе уравнение системы. Получаем линейное уравнение с переменной у: 4 ∙ 2 - 2у = 6, или 8 - 2у = 6, или -2у = -2, откуда у = 1. Пара чисел (2; 1) — решение системы (2), а следовательно, и равносильной системы (1).
Покажем, что системы (1) и (2) равносильны. Для системы (1) выполняется условие единственности решения: ![]()
Подставив найденное решение системы (2) х = 2, у = 1, убеждаемся, что оно является и решением системы (1). В равносильности систем (1) и (2) можно убедиться, используя и графический способ. Решим сначала графически систему (1). Построим график уравнения 3х + 2у = 8 (прямая I) и график уравнения 4х - 2у = 6 (прямая II). Эти прямые пересекаются в точке А. Координаты данной точки являются решением системы (1).
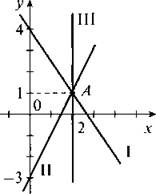
Теперь графически решим систему (2). Графиком уравнения 7х = 14 является прямая х = 2 (прямая III). Графиком второго уравнения 4х - 2у = 6 является прямая II. Видно, что прямые II и III пересекаются в той же точке А, т. е. координаты этой точки также будут решением системы (2). Следовательно, системы (1) и (2) равносильны.
Из разобранного примера видно, что при сложении уравнений системы получилось уравнение только с одной переменной. В качестве второго уравнения системы можно выбрать любое из уравнений данной системы. В результате таких преобразований была получена система, равносильная данной. В этом состоит суть метода сложения.
Пример 2
Решим систему уравнений ![]() способом сложения.
способом сложения.
В отличие от предыдущего примера в этом случае коэффициенты при у (а также при х) не являются противоположными числами. Поэтому сложение уравнений не позволит получить уравнение с одной переменной. Следовательно, необходимо добиться того, чтобы в уравнениях коэффициенты при любой переменной, например при у, стали противоположными числами.
Коэффициенты при у являются простыми числами 5 и 7. Поэтому умножим все члены первого уравнения на число 7, второго — на число -5. При этом уравнения являются равносильными, и система также равносильна данной: ![]()
В такой системе коэффициенты при у — противоположные числа. Сложим почленно левые и правые части уравнений системы и получим линейное уравнение с одной переменной: 21х - 35у - 10х + 35у = 63 - 85 или 11х = -22.
Запишем систему, равносильную данной. В качестве первого возьмем полученное уравнение, в качестве второго — первое уравнение данной системы. Получаем ![]()
Из первого уравнения найдем х = -2 и подставим это значение во второе уравнение. Получаем линейное уравнение с одной переменной: 3 ∙ (-2) - 5у = 9, или -6 - 5у = 9, или -5у = 9 + 6, или -5у = 15, откуда у = -3. Итак, данная система уравнений имеет единственное решение (-2; -3).
Пример 3
Решим систему уравнений ![]()
Избавимся теперь от переменной х. Коэффициенты при х в уравнениях — числа 6 и 4 — уже не являются простыми (это составные числа). Найдем их наименьшее общее кратное: НОК (6, 4) = 12. Так как 12 : 6 = 2 и 12 : 4 = 3, то умножим все члены первого уравнения на число 2, второго — на число -3. Получаем равносильную систему уравнений ![]()
Сложим почленно левые и правые части уравнений этой системы и получим линейное уравнение с переменной у: 12х + 10у - 12х + 9у = 14 - 33 или 19у = -19.
Запишем равносильную систему уравнений. В качестве первого выберем полученное уравнение, в качестве второго — второе уравнение данной системы. Получаем ![]()
Из первого уравнения найдем у = -1 и подставим это значение во второе уравнение. Получаем линейное уравнение с одной переменной: 4х - 3 ∙ (-1) = 11 или 4х = 8, откуда х = 2. Итак, данная система уравнений имеет единственное решение (2; -1).
Из рассмотренных примеров следует, что при решении систем линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают полученное уравнение с одной переменной;
4) находят соответствующее значение второй переменной.
Отметим, что если в уравнениях системы коэффициенты при одной из переменных являются противоположными числами, то при решении пункт 1 пропускают и начинают сразу с пункта 2.
Способ сложения можно использовать и при решении систем уравнений с параметрами.
Пример 4
Пусть (х0; у0) — решение системы ![]()
При каких значениях параметра а величина 2х0 + у0 ≥ 0?
Сначала решим данную систему способом сложения. Для этого умножим все члены первого уравнения на число -2 и получим равносильную систему ![]()
Сложим уравнения системы почленно. Получаем линейное уравнение с одной переменной: -4х - 6у + 4х + 5у = -10a - 8 + 9а + 6 или -у = -а - 2, откуда у = а + 2.
Подставим это значение у, например, в первое уравнение данной системы: 2х + 3(а + 2) = 5а + 4, или 2х + 3а + 6 = 5а + 4, или 2х = 5а + 4 - 3а - 6, или 2х = 2а - 2, откуда х = а - 1.
Итак, для каждого значения параметра а данная система уравнений имеет единственное решение х0 = а - 1, у0 = а + 2.
Найдем величину 2х0 + у0 = 2(а - 1) + (а + 2) = 2а - 2 + а + 2 = 3а.
По условию эта величина должна быть неотрицательной, т. е. 3а ≥ 0. Очевидно, что такое неравенство выполняется только при неотрицательных значениях а, т. е. при а ≥ 0.
IV. Задания на уроке
№ 1082 (а, в), 1084 (а, б, г), 1085 (в, г), 1087 (а, б), 1088, 1091, 1092 (а), 1093, 1095 (а, б).
V. Контрольные вопросы
— Какова основная цель при решении систем уравнений способом сложения?
— Как решить систему уравнений способом сложения? Объясните на примере.
VI. Творческие задания
— Выполните творческие задания 1 и 2 из предыдущего урока способом сложения.
VII. Подведение итогов уроков
Домашнее задание
№ 1082 (б, г), 1084 (в, д, е), 1085 (а, б), 1087 (в, г), 1089, 1090, 1092 (б), 1094, 1095 (в, г).