Итоговая контрольная работа - ПОДГОТОВКА К ИТОГОВОЙ КОНТРОЛЬНОЙ РАБОТЕ - ПОВТОРЕНИЕ КУРСА 7 КЛАССА

Цель: проверить знания, умения и навыки учащихся по базовым темам курса.

Ход урока

I. Сообщение темы и цели урока

II. Общая характеристика контрольной работы

Работа составлена в двух вариантах. Все задачи имеют примерно одинаковую сложность и контролируют основные умения:

1) проводить преобразования алгебраических выражений с использованием формул сокращенного умножения и вычислять их числовые значения;

2) решать линейные и нелинейные уравнения;

3) использовать свойства степени с натуральным показателем для вычисления значений числовых выражений;

4) строить графики линейных функций, определять принадлежность данной точки графику функции;

5) решать системы линейных уравнений и применять такие системы для решения текстовых задач.

Оценка “3” ставится за любые три решенные задачи, оценка “4” — за четыре задачи и оценка “5” — за пять задач. Одна задача дает учащимся некоторую свободу выбора.

III. Контрольная работа

Вариант 1

1. Упростите выражение и найдите его значение при а = 1 и b = 1/5.

2. Решите уравнение

3. Найдите значение выражения

4. Постройте график функции у = 3х - 6 и определите, проходит ли он через точки А (41; 117) и В (53; 152).

5. Сумма двух чисел равна 80, а сумма 50% первого числа и 25% второго числа равна 26. Найдите эти числа.

6. Решите уравнение

Вариант 2

1. Упростите выражение и найдите его значение при а = 2 и b = 1/5.

2. Решите уравнение

3. Найдите значение выражения

4. Постройте график функции у = 2х - 4 и определите, проходит ли он через точки А (43; 82) и В (56; 106).

5. Сумма двух чисел равна 90, а сумма 75% первого числа и 50% второго числа равна 61. Найдите эти числа.

6. Решите уравнение

IV. Разбор задач (ответы и решения)

Вариант 1

1. Используя формулы квадрата суммы и разности квадратов, упростим данное выражение. Получаем

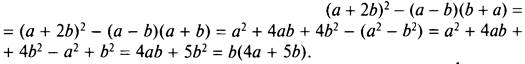
Найдем значение этого выражения при а = 1 и b = 1/5.

Получаем

(Ответ: 1.)

2. Умножим все члены уравнения на число 15. Получаем равносильное уравнение

или или 25х + 10 + 9х - 3 = 75, или 34х = 68, откуда х = 2.

(Ответ: х = 2.)

3. Учтем, что 3 ∙ 2 = 6, и используем свойства степеней. Получаем

(Ответ: 2.)

4. Построим график функции у = 3х - 6. Этим графиком будет прямая линия. Для построения найдем две точки, принадлежащие графику. Например, при х = 1 найдем у = 3 ∙ 1 - 6 = -3, при х = 2 найдем у = 3 ∙ 2 - 6 = 0. Таким образом, график проходит через точки С (1; -3) и D (2; 0). Отметим эти точки и проведем через них прямую.

Теперь определим, проходит ли она через точки А (41; 117) и В (53; 152). Найдем значение функции при х = 41 и получим у = 3 ∙ 41 - 6 = 123 - 6 = 117. Так как это значение равно ординате точки А, то график проходит через точку А.

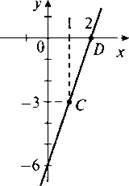
Найдем значение функции при х = 53 и получим у = 3 ∙ 53 - 6 = 159 - 6 = 153. Так как это значение не равно ординате точки В, то график не проходит через точку В.

(Ответ: проходит через точку А и не проходит через точку В.)

5. Пусть первое число равно х, а второе число равно у. По условию их сумма равна 80. Поэтому получаем первое уравнение х + у = 80. Один процент числа х равен x/100, тогда 50% числа х равны Один процент числа у равен у/100, тогда 25% числа у равны По условию сумма чисел x/2 и y/4 равна 26. Поэтому получаем второе уравнение

Имеем систему двух линейных уравнений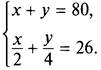

Решим систему способом подстановки. Из первого уравнения выразим у = 80 - х и подставим это выражение во второе уравнение. Получаем линейное уравнение с одним неизвестным Умножим все члены уравнения на число 4 и получим или 2х + 80 - х = 104, или х + 80 = 104, откуда х = 24. Используя формулу у = 80 - х, найдем у = 80 - 24 = 56.

(Ответ: первое число 24, второе число 56.)

6. Перенесем все члены уравнения (х - 2)(5х + 3) = (х - 2)(3х - 5) в левую часть и разложим их на множители. Получаем (х - 2)(5х + 3) - (х - 2)(3х - 5) = 0, или (х - 2)(5х + 3 - 3х + 5), или (х - 2)(2х + 8) = 0. Так как произведение двух множителей равно нулю, то один из этих множителей равен нулю. Получаем два линейных уравнения х - 2 = 0 (корень х = 2) и 2х + 8 = 0 (корень х = -4). Итак, данное уравнение имеет два корня: х = 2 и х = -4.

(Ответ: х = 2 и х = -4.)

Вариант 2

1. Используя формулы квадрата суммы и разности квадратов, упростим данное выражение. Получаем

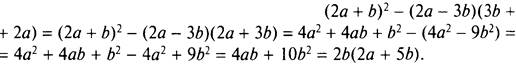
Найдем значение этого выражения при а = 2 и b = 1/5.

Получаем

(Ответ: 2.)

2. Умножим все члены уравнения на число 28. Получаем равносильное уравнение

или или 16х + 8 + 21х - 35 = 84, или 37х = 111, откуда х = 3.

(Ответ: х = 3.)

3. Учтем, что 5 ∙ 3 = 15, и используем свойства степеней. Получаем

(Ответ: 5.)

4. Построим график функции у = 2х - 4. Этим графиком будет прямая линия. Для построения найдем две точки, принадлежащие графику. Например, при х = 1 найдем у = 2 ∙ 1 - 4 = -2, при х = 2 найдем у = 2 ∙ 2 ∙ 4 = 0. Таким образом, график проходит через точки С (1; -2) и D (2; 0). Отметим эти точки и проведем через них прямую.

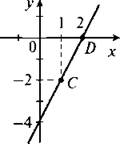
Теперь определим, проходит ли она через точки А (43; 82) и В (56; 106). Найдем значение функции при х = 43 и получим у = 2 ∙ 43 - 4 = 86 - 4 = 82. Так как это значение равно ординате точки А, то график проходит через точку А.

Найдем значение функции при x = 56 и получим у = 2 ∙ 56 - 4 = 112 – 4 = 108. Так как это значение не равно ординате точки В, то график не проходит через точку В.

(Ответ: проходит через точку А и не проходит через точку В.)

5. Пусть первое число равно x, а второе число равно у. По условию их сумма равна 90. Поэтому получаем первое уравнение х + у = 90. Один процент числа х равен x/100, тогда 75% числа х равны Один процент числа у равен y/100, тогда 50% числа у равны По условию сумма чисел 3/4х и у/2 равна 61. Поэтому получаем второе уравнение

Имеем систему двух линейных уравнений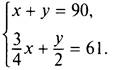

Решим систему способом подстановки. Из первого уравнения выразим у = 90 - х и подставим это выражение во второе уравнение. Получаем линейное уравнение с одним неизвестным Умножим все члены уравнения на число 4 и получим или 3х + (90 - х) ∙ 2 = 244 или 3х + 180 – 2x = 244 или х + 180 = 244, откуда х = 64. Используя формулу у = 90 - х, найдем у - 90 - 64 = 26.

(Ответ: первое число 64, второе число 26.)

6. Перенесем все члены уравнения (х - 3)(6х + 5) = (х - 3)(2х - 3) в левую часть и разложим их на множители. Получаем (х - 3)(6х + 5) - (х - 3)(2х - 3) = 0, или (х - 3)(6х + 5 - 2х + 3) = 0, или (х - 3)(4х + 8) = 0. Так как произведение двух множителей равно нулю, то один из этих множителей равен нулю. Получаем два линейных уравнения х - 3 = 0 (корень х = 3) и 4х + 8 = 0 (корень х = - 2). Итак, данное уравнение имеет два корня: х = 3 и х = -2.

(Ответ: х = 3 и х = -2.)