Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
РЕШЕНИЕ ЗАДАЧ - Урок 5 - ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
|
Цель деятельности учителя |
Создать условия для приведения в систему знаний учащихся по данной теме, четкого понимания учащимися того, когда в задаче нужно применить признак параллельности двух прямых, а когда - свойство параллельных прямых |
||
|
Термины и понятия |
Параллельные прямые, аксиома, свойства параллельных прямых |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют работать с геометрическим текстом, анализировать его, извлекать необходимую информацию |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют работать в сотрудничестве с учителем. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные ресурсы |
• Карточки для устного опроса. • Чертежи к задачам |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Систематизировать теоретические знания учащихся |
(Ф/И) 1. Обсуждение результатов проверочной работы и анализ допущенных ошибок. 2. Проверка правильности выполнения домашней работы. Для этого к доске вызываются трое учащихся и демонстрируют решения домашних задач. 3. Устный опрос учащихся по карточкам (см. Ресурсный материал) |
||
|
II этап. Решение задач по готовым чертежам |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Совершенствовать навыки решения простейших задач |
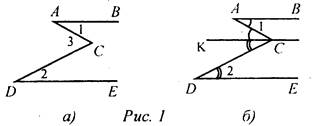
(И) 1. Решить задачи по готовым чертежам, сделав в тетрадях краткие записи (см. Ресурсный материал) (самостоятельно). (Ф/И) 2. Решить задачу (один ученик решает у доски, остальные в тетрадях). Дано: АВ || DE (рис. 1а). Доказать: ∠1 + ∠2 = ∠3.
Подсказка: через точку С проведите прямую, параллельную АВ. Доказательство (см. рис. 16): 1) Через точку С, не лежащую на прямой АВ, можно провести прямую, параллельную АВ, и притом только одну. 2) Так как КС || АВ, a АВ || DE по условию задачи, то КС || DE. 3) ∠1 = ∠ACK, как накрест лежащие при параллельных прямых АВ и КС и секущей АС. 4) ∠2 = ∠KCD, как накрест лежащие при параллельных прямых КС и DE и секущей DC. Так как ∠1 = ∠ACK, ∠2 = ∠KCD, a ∠3 = ∠ACK + ∠KCD, то ∠3 = ∠1 + ∠2, что и требовалось доказать |
||
|
III этап. Самостоятельное решение задач |
|||
|
Цель деятельности |
Задания для самостоятельной работы |
||
|
Совершенствовать навыки решения задач |
(И) Учащимся предложены задачи двух уровней сложности (см. Ресурсный материал). Они сами выбирают, задачи какого уровня будут решать. В конце урока тетради можно собрать на проверку |
||
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Что повторили на уроке? - Оцените свою работу на уроке |
(И) Домашнее задание: решить № 207 |
||
Ресурсный материал
Карточки для устного опроса
Вариант I
1. Сформулируйте один из признаков параллельности двух прямых.
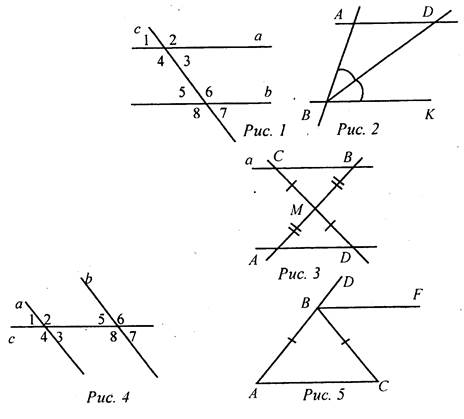
2. Докажите, что прямые а и b, изображенные на рисунке 1, параллельны, если ∠1 = 36°; ∠8 = 144°.
3. На рисунке 2 прямые AD и ВК параллельны, луч BD - биссектриса угла АВК, ∠ABK = 80°. Найдите углы треугольника ABD.
Вариант II
1. Сформулируйте аксиому параллельных прямых.
2. Дан треугольник CDE. Сколько прямых, параллельных стороне СЕ, можно провести через вершину D?
3. На рисунке 3 отрезки АВ и CD пересекаются в их общей середине М. Через точку В проведена прямая а, параллельная прямой AD. Докажите, что прямая а проходит через точку С.
Вариант III
1. Сформулируйте одно из свойств параллельных прямых.
2. На рисунке 4 прямые а и b параллельны; ∠2 = 132°. Найдите ∠7.
3. На рисунке 5 АВ = ВС; BF || АС. Докажите, что луч биссектриса угла CBD.
Задачи на готовых чертежах для самостоятельного решения
Вариант I
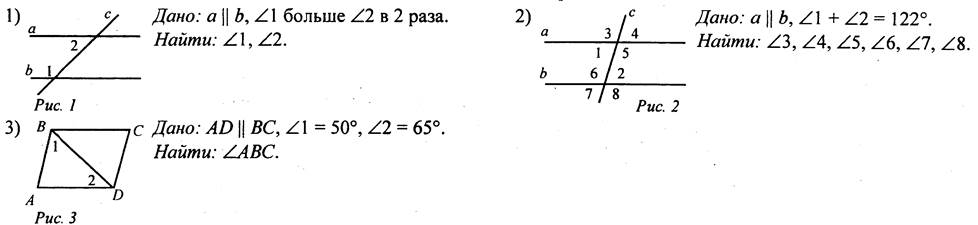

Вариант II

Ответы для самопроверки:
![]()
Самостоятельная работа
I уровень
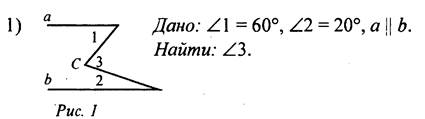
Решение: через точку С провести прямую, параллельную прямой а, и доказать, что ∠3 = ∠1 + ∠2, ∠3 = 80°.
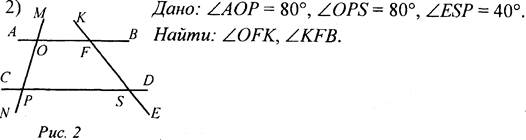
Решение: ∠AOP = ∠OPS, тогда AB || CD, тогда ∠OFK = 40°, ∠KEB = 140°.
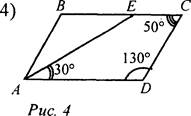
Дано: AE - биссектриса ∠BAD.
Найти: ∠ABE, ∠BEA.
II уровень

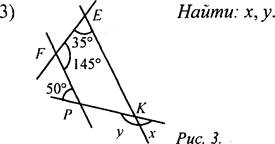
Найти: x, у.
Указание: докажите, что РЕ || KF из равенства углов, градусные меры которых 70°, тогда у = 52°, х = 128°.
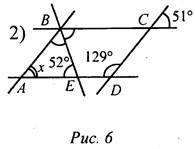
Найти: х, если ∠ABE = ∠CBE.
Решение:
∠C + ∠D = 180°, значит, ВС || AD, тогда ∠AEB = ∠EBC = 52°. ∠ABE = ∠CBE, поэтому ∠ABC = 104°. Так как ВС || AD, a ∠ABC = 104°, то ∠BAE = 76°, то есть х = 76°.
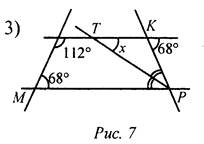
Дано: РТ - биссектриса ∠KPM.
Найти: х.
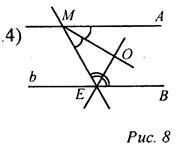
Дано: a || b.
Доказать: ∠MOE = 90°.
Указание: Через точку О провести прямую, параллельную прямой МА, и доказать ∠MOE = ∠AMO + ∠OEB.