Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
АНАЛИЗ ОШИБОК КОНТРОЛЬНОЙ РАБОТЫ - Урок 2 - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
|
Цель деятельности учителя |
Совершенствовать навыки решения задач; развивать навыки самопроверки выполненных работ, умение находить свои ошибки; создать условия для устранения пробелов в знаниях учащихся |
|||
|
Термины и понятия |
Треугольник, неравенство треугольника, соотношения между сторонами и углами треугольника |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость геометрических знаний в жизни человека |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Задания для индивидуальной работы |
|||
|
I этап. Общий анализ контрольной работы |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Устранение пробелов в знаниях учащихся |
(Ф/И) 1. Общее впечатление о выполненной работе. 2. Решение (или обсуждение) задач, с которыми не справились большинство учащихся. 3. Демонстрация лучших работ |
|||
|
II этап. Выполнение работы над ошибками |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Совершенствовать навыки решения задач |
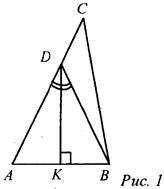
(Ф/И) 1. Найти свои ошибки в решениях задач и устранить их с помощью учителя или ученика, справившегося с работой. 2. Решить задачи другого варианта. Если ученик выполнил контрольную работу - решает дополнительные задачи. Дополнительные задачи. Задача 1. Через точку К, взятую на стороне АВ треугольника АВС, проведена прямая, перпендикулярная АВ и пересекающая сторону АС в точке D. Известно, что ∠KDB = ∠KDA, АС = 30 см, ВС = 15 см. Найдите периметр треугольника BDC.
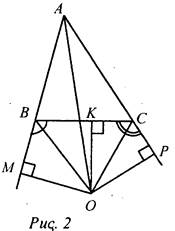
Решение: ΔADK = ΔBDK по катету и прилежащему к нему острому углу, следовательно, AD = BD. РBDC = BD + DC + СВ = (AD + DC) + СВ = АС + СВ = 30 см + 15 см = 45 см. Ответ: РBDC = 45 см. Задача 2. Докажите, что биссектриса угла А треугольника АВС проходит через точку пересечения прямых, содержащих биссектрисы внешних углов при вершинах В и С.
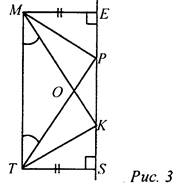
Доказательство: ВО и СО - биссектрисы ∠MBC и ∠PCB соответственно. Докажем, что АО - биссектриса ∠BAС. Проведем ОМ ⊥ AB, OK ⊥ ВС, OP ⊥ АС, тогда ΔВОМ = ΔВОК, ΔСОК = ΔСОР по гипотенузе и острому углу. Следовательно, ОМ = OK = ОР. ΔАОМ = ΔАОР по катету и гипотенузе, отсюда ΔМАО = ΔРАО, то есть АО - биссектриса ∠BAC. Задача 3. Дано: точки М и T равноудалены от прямой РК, ∠KMT = ∠PTM. Доказать: ΔРМК = ΔРКТ.
Доказательство: ∠KMT = ∠PTM, тогда ∠EMK = ∠STP, значит, ΔЕМК = ΔSTP по катету и прилежащему к нему острому углу, следовательно, ∠MKP = ∠TPK, а МК = TP. ΔРМК = ΔКТР по двум сторонам и углу между ними |
|||
|
III этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя Деятельность учащихся |
||||
|
(Ф/И) - Какие темы вызвали у вас наибольшее затруднение? |
(И) Домашнее задание: повторить главу I, вопросы 1-21 |
|||