Дидактические материалы по геометрии 8 класс к учебнику Л. С. Атанасяна Геометрия 7-9 классы - 2017 год
КОНТРОЛЬНЫЕ РАБОТЫ
КОНТРОЛЬНАЯ РАБОТА № 1 . Четырехугольники
Задачи для подготовки к контрольной работе
1. На рисунке ABCD параллелограмм, причем АВ ≠ ВС, KMNP — ромб. Укажите номера верных утверждений:
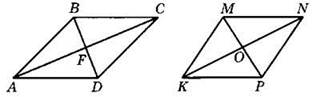
1) AF = FC
2) MO = OP
3) ΔABF — прямоугольный
4) ΔMKO — прямоугольный
5) ΔKMN — равнобедренный
6) ΔABD — равнобедренный
7) ∠BAF = ∠FAD
8) ∠MKO = ∠OKP
9) AF — медиана треугольника ABD
10) КО — медиана треугольника КМР
11) AF — высота треугольника ABD
12) КО — высота треугольника КМР
2. Один из углов ромба ABCD на 40° больше другого. Найдите углы треугольника ВОС, если О — точка пересечения диагоналей.
3. Диагонали прямоугольника CDEF пересекаются в точке К. Найдите стороны прямоугольника, если его периметр равен 28 см, а периметры треугольников CDK и DEK равны 16 см и 18 см.
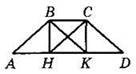
4. На рисунке ABCD — трапеция, ВСКН — прямоугольник, его диагонали параллельны боковым сторонам трапеции.
1) Докажите, что ΔАВК — равнобедренный.
2) Докажите, что AD = 3ВС.
5. На рисунке ΔАВС — равнобедренный, точки D и F — середины боковых сторон, Е — точка на основании, DE || ВС, ЕF || АВ. Определите вид четырехугольника DBFE и найдите его периметр, если АВ = 18 см.

6. Диагонали трапеции ABCD являются биссектрисами ее углов при большем основании AD.
1) Докажите, что трапеция ABCD — равнобедренная.
2) Докажите, что ΔAOD — равнобедренный (О — точка пересечения диагоналей).
7. Постройте фигуру, симметричную трапеции ABCD относительно:
а) вершины С; б) прямой АС.
ВАРИАНТ 1
Часть 1
Запишите номера верных ответов к заданию 1.
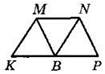
1°. На рисунке KMNP — трапеция, BN || КМ, ВМ || NP, MN = NP, MN ≠ КМ. Укажите верные утверждения:
1) KMNB — параллелограмм
2) KMNB — ромб
3) MNPB — ромб
4) ∠KBM = ∠MBN
5) ∠MBN = ∠NBP

Часть 2
Запишите ответ к заданиям 2 и 3.
2°. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите периметр треугольника AOD, если АВ = 9, ВС = 12, BD = 15.
3°. Одна из сторон параллелограмма в 3 раза больше другой. Найдите длину меньшей стороны, если периметр параллелограмма равен 32 см.
Часть 3
Запишите обоснованное решение задач 4—6.
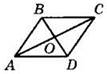
4°. На рисунке ABCD — ромб, ∠ABC = 140°. Найдите углы треугольника COD.
5. Начертите произвольный треугольник DEF, на стороне DE отметьте точку А, не являющуюся ее серединой. Постройте фигуру, симметричную треугольнику DEF относительно точки А.
6. В параллелограмме BCDE биссектриса угла В пересекает сторону DE в точке К, причем DK = 4, ЕК = 12. Найдите периметр параллелограмма.
ВАРИАНТ 2
Часть 1
Запишите номера верных ответов к заданию 1.
1°. На рисунке KMNP — трапеция, BN || КМ, ВМ || NP, MN = КМ, MN ≠ NP. Укажите верные утверждения:
1) KMNB — параллелограмм
2) KMNB — ромб
3) MNPB — ромб
4) ∠KBM = ∠MBN
5) ∠MBN = ∠NBP
Часть 2
Запишите ответ к заданиям 2 и 3.
2°. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите периметр треугольника АОВ, если AD = 15, CD = 8, АС = 17.
3°. Одна из сторон параллелограмма в 4 раза больше другой. Найдите длину меньшей стороны, если периметр параллелограмма равен 30 см.
Часть 3
Запишите обоснованное решение задач 4-6.
4°. На рисунке ABCD — ромб, ∠BAD = 100°. Найдите углы треугольника AOD.

5. Начертите прямоугольник МРОК. Постройте фигуру, симметричную ему относительно прямой ОМ.
6. В параллелограмме BCDE биссектриса угла С пересекает сторону DE в точке К, причем ЕК = 7, DK = 11. Найдите периметр параллелограмма.
ВАРИАНТ 3
Часть 1
Запишите номера верных ответов к заданию
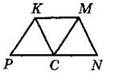
1°. На рисунке KMNP — трапеция, СМ || РК, СК || МАГ, MN = КМ, КМ ≠ КР. Укажите верные утверждения:
1) РКМС — параллелограмм
2) РКМС — ромб
3) CKMN — ромб
4) ∠KCM = ∠MCN
5) ∠PCK = ∠KCM
Часть 2
Запишите ответ к заданиям 2 и 3.
2°. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите периметр треугольника ВОС, если АВ = 15, AD = 20, ВО = 25.
3°. Одна из сторон параллелограмма в 5 раз больше другой. Найдите длину меньшей стороны, если периметр параллелограмма равен 36 см.
Часть 3
Запишите обоснованное решение задач 4—6.
4°. На рисунке ABCD — ромб, ∠ABC = 120°. Найдите углы треугольника ВОС.
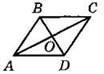
5. Начертите прямоугольный треугольник АВС, на гипотенузе АВ отметьте точку N, не являющуюся ее серединой. Постройте фигуру, симметричную треугольнику АВС относительно точки N.
6. В параллелограмме BCDE биссектриса угла D пересекает сторону ВС в точке М, причем ВМ = 7, МС = 10. Найдите периметр параллелограмма.
ВАРИАНТ 4
Часть 1
Запишите номера верных ответов к заданию 1.
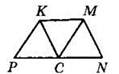
1°. На рисунке KMNP — трапеция, СК || MN, СМ || РК, РК = КМ, MN ≠ КМ. Укажите верные утверждения:
1) РКМС — параллелограмм
2) РКМС — ромб
3) CKMN — ромб
4) ∠KCM = ∠MCN
5) ∠PCK = ∠KCM
Часть 2
Запишите ответ к заданиям 2 и 3.
2°. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите периметр треугольника COD, если АВ = 5, ВС = 12, BD = 13.
3°. Одна из сторон параллелограмма в 2 раза больше другой. Найдите длину меньшей стороны, если периметр параллелограмма равен 42 см.
Часть 3
Запишите обоснованное решение задач 4—6.
4°. На рисунке ABCD — ромб, ∠BAD = 160°. Найдите углы треугольника АОВ.

5. Начертите параллелограмм MNPR. Постройте фигуру, симметричную ему относительно прямой РМ.
6. В параллелограмме BCDE биссектриса угла Е пересекает сторону ВС в точке H, причем ВН = 9, СН = 8. Найдите периметр параллелограмма.
КОНТРОЛЬНАЯ РАБОТА № 2 . Теорема Пифагора. Площадь
Задачи для подготовки к контрольной работе
1. ABCD — трапеция. Используя данные, указанные на рисунке, найдите:
а) большее основание трапеции
б) площадь треугольника ACD
в) площадь четырехугольника АВСМ, если АВ || СМ
г) площадь трапеции АВСН

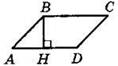
2. Найдите периметр параллелограмма ABCD, изображенного на рисунке, если ВН — его высота, площадь параллелограмма равна 120 м2, АН = 6 м, DH = 9 м.
3. Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.
4. На рисунке треугольник АВС — равнобедренный с основанием АС, AD — его высота, BD = 16 см, DC = 4 см. Найдите основание АС и высоту AD.
5. Найдите катет прямоугольного треугольника, если он в 2 раза меньше гипотенузы, а второй катет равен 6 м.
6. На рисунке отрезок МК перпендикулярен двум сторонам ромба ABCD и проходит через точку О пересечения его диагоналей. Найдите длину отрезка МК, если диагонали ромба равны 32 и 24.
7. Диагонали прямоугольника ABCD пересекаются в точке О. Перпендикуляр AM, опущенный на диагональ BD, разбивает отрезок ОБ на части: ОМ = 12 см и ВМ = 3 см. Чему равны перпендикуляр AM и сторона АВ?
ВАРИАНТ 1
Часть 1
Запишите номера верных ответов к заданию 1.
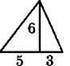
1°. Используя данные, указанные на рисунке, найдите площадь треугольника.
1) 24
2) 48
3) 14
4) 30
Часть 2
Запишите ответ к заданию 2.
2°. Стороны прямоугольника 5 см и 12 см. Чему равна диагональ?
Часть 3
Запишите обоснованное решение задач 3—5.
3°. Боковая сторона равнобедренного треугольника равна 15 см, а высота, проведенная к основанию, 9 см. Найдите основание треугольника.
4. Найдите площадь равнобедренной трапеции, если ее основания равны 5 см и 17 см, а боковая сторона равна 10 см.
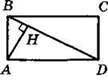
5. На рисунке ABCD — прямоугольник, AH ⊥ BD, сторона АВ в 3 раза меньше стороны ВС. Найдите АН, если BD = 20.
ВАРИАНТ 2
Часть 1
Запишите номера верных ответов к заданию 1.
1°. Используя данные, указанные на рисунке, найдите площадь треугольника.
1) 42
2) 13
3) 21
4) 28
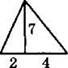
Часть 2
Запишите ответ к заданию 2.
2°. Одна из сторон прямоугольника равна 8 см, а диагональ 17 см. Чему равна вторая сторона прямоугольника?
Часть 3
Запишите обоснованное решение задач 3—5.
3°. Найдите сторону ромба, если его диагонали равны 12 см и 16 см.
4. Найдите площадь равнобедренной трапеции, если ее меньшее основание равно 7 см, боковая сторона — 13 см, высота — 12 см.
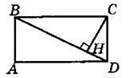
5. На рисунке ABCD — прямоугольник, CH ⊥ BD, сторона АВ в 3 раза меньше диагонали. Найдите СН, если ВС = 20.
ВАРИАНТ 3
Часть 1
Запишите номера верных ответов к заданию 1.
1°. Используя данные, указанные на рисунке, найдите площадь треугольника.
1) 18
2) 72
3) 42
4) 36

Часть 2
Запишите ответ к заданию 2.
2°. Стороны прямоугольника 12 см и 16 см. Чему равна диагональ?
Часть 3
Запишите обоснованное решение задач 3—6.
3°. Сторона ромба равна 17 см, одна из диагоналей равна 30 см. Найдите вторую диагональ.
4. Найдите площадь равнобедренной трапеции, если ее основания равны 6 см и 16 см, а боковая сторона равна 13 см.
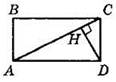
5. На рисунке ABCD — прямоугольник, DH ⊥ AC, сторона АВ в 2 раза меньше стороны ВС. Найдите DH, если АС = 10.
ВАРИАНТ 4
Часть 1
Запишите номера верных ответов к заданию 1.
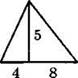
1°. Используя данные, указанные на рисунке, найдите площадь треугольника.
1) 17
2) 60
3) 30
4) 44
Часть 2
Запишите ответ к заданию 2.
2°. Одна из сторон прямоугольника равна 12 см, а диагональ 15 см. Чему равна вторая сторона прямоугольника?
Часть 3
Запишите обоснованное решение задач 3—5.
3°. Высота равнобедренного треугольника, проведенная к основанию, равна 5 см, а основание 24 см. Найдите боковую сторону.
4. Найдите площадь равнобедренной трапеции, если ее меньшее основание равно 7 см, боковая сторона — 10 см, высота — 8 см.
5. На рисунке ABCD — прямоугольник, ВН ⊥ АС, сторона АВ в 5 раз меньше диагонали. Найдите ВН, если AD = 12.
КОНТРОЛЬНАЯ РАБОТА № 3 . Подобные треугольники
Задачи для подготовки к контрольной работе
1. Используя данные, указанные на рисунке, найдите площадь треугольника АВС.
2. Боковая сторона равнобедренной трапеции равна 6, а острый угол при основании равен а. Найдите большее основание трапеции, если меньшее основание равно 5.
Указание. В задачах 3-5 докажите подобие треугольников и, используя данные, указанные на рисунках, вычислите искомые элементы.
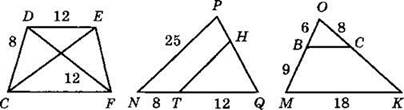
3. Найдите CF, если CDEF — трапеция.
4. Найдите ТН, если ТН || NP.
5. Найдите ВС, если ВС || МК.
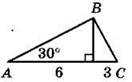
6. Найдите тангенс угла при основании равнобедренного треугольника с основанием 30 см и боковой стороной 25 см.
7. AM и ВК — медианы треугольника АВС. Определите вид четырехугольника АВМК и найдите его периметр, если АВ = 14, ВС = 12, АС = 18.
8. На рисунке треугольник МОР — равнобедренный, ОР — его основание, МК и ОН — высоты. Докажите, что треугольники МОК и МСН подобны и найдите СН, если МН = 6, PH = 4, ОР = 12.

9. На рисунке ABCD — ромб, ВН — его высота. Используя данные, указанные на рисунке, найдите длины отрезков ВК и КН.

ВАРИАНТ 1
Часть 1
Запишите номера верных ответов к заданиям 1 и 2.
1°. В прямоугольнике ABCD угол АСВ равен β, диагональ равна 12. Найдите сторону АВ.
![]()
2°. В треугольнике BCD угол С — прямой, BD = 13 м, ВС = 12 м. Найдите длину средней линии МК, если М ∈ BD, К ∈ ВС.
1) 5
2) 6
3) 6,5
4) 2,5
Часть 2
Запишите ответ к заданиям 3 и 4.
3°. Найдите длину отрезка МВ, если в изображенной на рисунке трапеции MNPK известно: МК = 24, NP = 18, ВР = 12.
4°. В равнобедренном треугольнике основание равно 20, а угол между боковыми сторонами равен 120°. Найдите высоту, проведенную к основанию.
Часть 3
Запишите обоснованное решение задач 5 и 6.
5. На рисунке отрезки AM и ВН являются высотами треугольника АВС. Докажите, что треугольники СВН и САМ подобны.

6. В прямоугольном треугольнике BCD из точки М, лежащей на гипотенузе ВС, опущен перпендикуляр MN на катет BD. Найдите синус угла В, если MN = 12, CD = 18, МС = 8.
ВАРИАНТ 2
Часть 1
Запишите номера верных ответов к заданиям 1 и 2.
1°. Диагональ прямоугольника ABCD равна 16, угол CBD равен α. Найдите сторону ВС.
![]()
2°. В треугольнике BDE угол D — прямой, BD = 9 м, DE = 12 м. Найдите длину средней линии РМ, если М ∈ DE, Р ∈ BD.
1) 4,5
2) 6
3) 7,5
4) 15
Часть 2
Запишите ответ к заданиям 3 и 4.
3°. Найдите длину отрезка СО, если в изображенной на рисунке трапеции КМОР известно: МО = 12, КР = 20, СК = 16.

4°. Найдите основание равнобедренного треугольника, если угол при основании равен 30°, а высота, проведенная к основанию, равна 10.
Часть 3
Запишите обоснованное решение задач 5 и 6.
5. На рисунке отрезки АК и ВЫ являются высотами треугольника АВС. Докажите, что треугольники ВОК и ВСМ подобны.
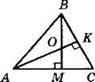
6. В треугольнике АВС прямая, параллельная стороне ВС, пересекает высоту АН в точке К и сторону АС в точке М. Найдите косинус угла С, если МК = 16, СН = 20, МС = 5.
ВАРИАНТ 3
Часть 1
Запишите номера верных ответов к заданиям 1 и 2.
1°. Диагональ прямоугольника ABCD равна 14, угол АСВ равен γ. Найдите сторону ВС.
![]()
2°. В треугольнике МРК угол Р — прямой, МР = 3 м, РК = 4 м. Найдите длину средней линии ВС, если В ∈ МР, С ∈ РК.
1) 2,5
2) 2
3) 1,5
4) 5
Часть 2
Запишите ответ к заданиям 3 и 4.
3°. Найдите основание CD изображенной на рисунке трапеции BCDE, если СК = 12, КЕ = 16, BE = 20.
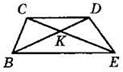
4°. Высота, проведенная к основанию равнобедренного треугольника, равна 8, а угол при основании равен 30°. Найдите основание треугольника.
Часть 3
Запишите обоснованное решение задач 5 и 6.
5. На рисунке отрезки CN и ВК являются высотами треугольника АВС. Докажите, что треугольники BNP и ВКА подобны.

6. В прямоугольном треугольнике CDE из точки N, лежащей на гипотенузе CD, опущен перпендикуляр NP на катет СЕ. Найдите косинус угла С, если CN = 9, ND = 6, РЕ = 4.
ВАРИАНТ 4
Часть 1
Запишите номера верных ответов к заданиям 1 и 2.
1°. Диагональ прямоугольника ABCD равна 10, угол ВАС равен β. Найдите сторону ВС.
![]()
2°. В треугольнике КРН угол H — прямой, РК = 17 м, КН = 15 м. Найдите длину средней линии ВС, если В ∈ КН, С ∈ РК.
1) 8
2) 4
3) 8,5
4) 7,5
Часть 2
Запишите ответ к заданиям 3 и 4.
3°. Найдите основание CF изображенной на рисунке трапеции CDEF, если известно, что DO = 9, DE = 15, OF = 12.
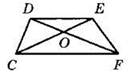
4°. Найдите основание равнобедренного треугольника, если высота, проведенная к основанию, равна 6, а угол между боковыми сторонами равен 120°.
Часть 3
Запишите обоснованное решение задач 5 и 6.
5. На рисунке отрезки AN и ВР являются высотами треугольника АВС. Докажите, что треугольники АОР и ACN подобны.

6. В треугольнике АВС прямая, параллельная стороне АВ, пересекает высоту СН в точке М и сторону АС в точке К. Найдите косинус угла А, если МК = 12, АН = 20, АК = 10.
КОНТРОЛЬНАЯ РАБОТА № 4 . Окружность
Задачи для подготовки к контрольной работе
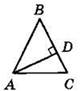
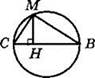
1. Найдите периметр треугольника АОВ, если прямая АВ касается в точке А окружности с центром О и радиусом 6 см, а длина отрезка АВ равна 8 см.
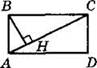
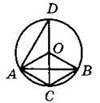
2. На рисунке О — центр окружности, вписанной в треугольник ABD, М, N и К — точки касания окружности со сторонами. Укажите номера верных утверждений:
1) ВР — медиана треугольника ABD
2) ВР — биссектриса треугольника ABD
3) ВР — высота треугольника ABD
4) ВМ = BN
5) AM = ВМ
6) ON ⊥ BD
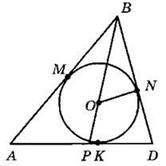
3. В окружности с центром О проведены хорды АВ и CD.
1) Найдите ∠BDC, если ∠ACD = 15°, АВ ⊥ CD.
2) Найдите ∠AOD, если
a) ∠ACD = 15°; б) ∠ACD = 95°.
3) Найдите ∠ACD, если хорда АВ проходит через центр О, ∠BCD = 20°.
4. Две хорды пересекаются в точке, которая делит одну из них на отрезки 8 м и 9 м. На какие отрезки разделилась вторая хорда, если она равна 22 м?
5. Прямоугольный треугольник MKL вписан в окружность радиуса 13 см. Найдите длину высоты МН, опущенной на наибольшую сторону треугольника, если HL = 8 см.
6. На рисунке АВ и АС — касательные к окружности с центром О. Найдите длину отрезка АВ, если АС = 24 см, а отрезок ВМ в 2 раза больше отрезка СМ.
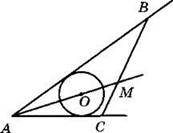
7. На рисунке О — центр окружности, АОВС — ромб. Найдите ∠ADC.
ВАРИАНТ 1
Часть 1
Запишите номера верных ответов к заданиям 1 и 2.
1°. К окружности с центром О проведены касательные СА и СВ (А и В — точки касания). Найдите ∠AOC, если ∠ACB = 50°.
1) 25°
2) 50°
3) 40°
4) 65°
2°. На рисунке ∠C = 30°, ∠AEC = 110°. Найдите ∠CBD.
1) 30°
2) 40°
3) 110°
4) 140°

Часть 2
Запишите ответ к заданиям 3 и 4.
3°. Прямоугольный треугольник с катетами 12 см и 16 см вписан в окружность. Найдите ее радиус.
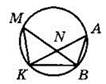
4°. Хорды АВ и CD пересекаются в точке Е. Найдите длину отрезка АЕ, если он в 2 раза меньше отрезка BE, СЕ = 8, DE = 9.
Часть 3
Запишите обоснованное решение задач 5 и 6.
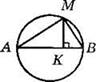
5. На рисунке АВ — диаметр окружности, МК ⊥ АВ. Найдите длину хорды AM, если АК = 9 см, ВК = 3 см.
6. Треугольник DBC — равнобедренный с основанием DC. Его периметр равен 34 см, BD = 10 см. Найдите длину отрезка BN (N — точка касания вписанной окружности со стороной DB).

ВАРИАНТ 2
Часть 1
Запишите номера верных ответов к заданиям 1 и 2.
1°. К окружности с центром О проведены касательные МК и МР (К и Р — точки касания). Найдите ∠KMP, если ∠KOM = 70°.
1) 70°
2) 20°
3) 40°
4) 140°
2°. На рисунке ∠M = 55°, ∠KNM = 60°. Найдите ∠ABM.
1) 65°
2) 60°
3) 55°
4) 115°
Часть 2
Запишите ответ к заданиям 3 и 4.
3°. В окружности с радиусом 7,5 см проведены диаметр АС и хорда АК, равная 9 см. Найдите длину хорды СК.
4°. Две хорды одной окружности пересекаются в точке, делящей одну хорду на отрезки 2 см и 16 см, а другую — на отрезки, один из которых в 2 раза больше другого. Найдите длину второй хорды.
Часть 3
Запишите обоснованное решение задач 5 и 6.
5. Найдите периметр треугольника АВС, изображенного на рисунке, если точка О — центр вписанной окружности, ВМ = 6 см, МС = 8 см, АС = 12 см.
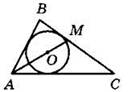
6. Треугольник МРК равнобедренный, его основание МК равно 16 м, а периметр равен 52 м. Найдите длину отрезка АР (А — точка касания вписанной окружности со стороной МР).
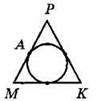
ВАРИАНТ 3
Часть 1
Запишите номера верных ответов к заданиям 1 и 2.
1°. К окружности с центром О проведены касательные АВ и АС (В и С — точки касания). Найдите ∠BAC, если ∠AOC = 50°.
1) 80°
2) 40°
3) 50°
4) 100°
2°. На рисунке ∠B = 30°, ∠BAD = 70°. Найдите ∠BCE.
1) 30°
2) 70°
3) 100°
4) 80°

Часть 2
Запишите ответ к заданиям 3 и 4.
3°. В окружность радиуса 10 см вписан прямоугольный треугольник, один катет которого равен 16 см. Найдите второй катет.
4°. Точка пересечения двух хорд окружности делит одну хорду на отрезки 3 см и 16 см, а вторую — на отрезки, один из которых в 3 раза больше другого. Найдите длину второй хорды.
Часть 3
Запишите обоснованное решение задач 5 и 6.
5. Найдите периметр треугольника АВС, изображенного на рисунке, если точка О — центр вписанной окружности, АК = 10 см, СК = 15 см, АВ = 12 см.
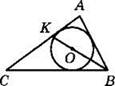
6. Треугольник АВЕ — равнобедренный с основанием АЕ. Его периметр равен 64 см, BE = 20 см. Найдите длину отрезка ВМ (М — точка касания вписанной окружности со стороной BE).

ВАРИАНТ 4
Часть 1
Запишите номера верных ответов к заданиям 1 и 2.
1°. К окружности с центром О проведены касательные ВА и ВС (А и С — точки касания). Найдите ∠AOB, если ∠AВС = 80°.
1) 80°
2) 50°
3) 100°
4) 40°
2°. На рисунке ∠D = 30°, ∠ACD = 100°. Найдите ∠MKD.
1) 30°
2) 50°
3) 100°
4) 130°
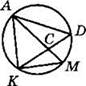
Часть 2
Запишите ответ к заданиям 3 и 4.
3°. В окружности проведены диаметр KN и две хорды ВК = 8 см и BN = 6 см. Чему равен радиус окружности?
4°. Хорды MN и РК пересекаются в точке С. Найдите длину отрезка СР, если он в 5 раз больше отрезка СК, МС = 5, CN = 9.
Часть 3
Запишите обоснованное решение задач 5 и 6.
5. На рисунке ВС — диаметр окружности, МН ⊥ ВС. Найдите длину хорды МС, если ВН = 6 см, СН = 2 см.
6. Периметр равнобедренного треугольника MRS равен 66 м, а основание MS равно 26 м. Найдите длину отрезка AR (А — точка касания вписанной окружности со стороной MR).

КОНТРОЛЬНАЯ РАБОТА № 5. ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА
Задачи для подготовки к контрольной работе
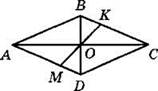
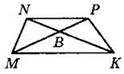
1. Диагонали четырехугольника ABCD пересекаются в точке О. Укажите верные утверждения для каждого из случаев, когда четырехугольник ABCD является: а) параллелограммом произвольного вида; б) ромбом; в) прямоугольником.
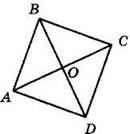
1) АО = ОС
2) АО ⊥ ВО
3) АВ = ВС
4) АВ = CD
5) АС = BD
6) ∠ABC = ∠ADC
7) ∠ABC = ∠BCD
8) ∠ABO = ∠CBO
2. Используя данные, указанные на рисунке, найдите:
а) площадь треугольника CDE;
б) площадь параллелограмма ABCD;
в) площадь трапеции АВСЕ.

3. Прямая МК касается в точке М окружности с центром О, причем МК = 22. Найдите радиус окружности и длину отрезка О К, если ∠MOK = 60°.
4. Найдите площадь ромба, если известно, что его сторона равна m, а острый угол равен α.
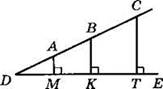
5. На рисунке AM, ВК и СТ — перпендикуляры к прямой DE, а отрезки DA, АВ и BС относятся, как 2 : 2 : 3. Найдите длины перпендикуляров AM и ВК, если СТ = 28 см.
6. Площадь прямоугольного треугольника равна 24 см2, а один из катетов равен 6 см. Найдите длину средней линии, параллельной другому катету.
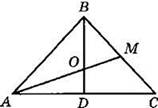
7. На рисунке треугольник АВС — равнобедренный с основанием АС, BD — его высота. Найдите боковую сторону треугольника, если АО = 18 см, ОМ = 12 см, ВМ = 16 см.
ВАРИАНТ 1
Часть 1
Запишите номера верных ответов к заданиям 1—3.
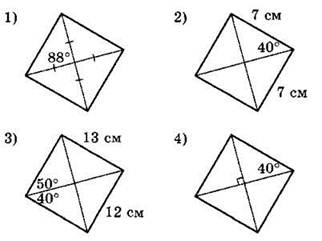
1°. На каждом из приведенных ниже рисунков изображен параллелограмм, обладающий теми или иными свойствами. Используя данные, приведенные на рисунках, укажите номера тех рисунков, на которых изображен ромб.
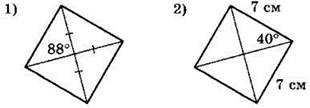
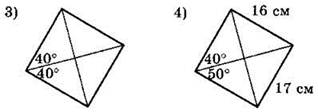
2°. Используя данные, указанные на рисунке, найдите площадь изображенной ниже равнобедренной трапеции.
1) 96
2) 48
3) 72
4) 36

3°. Найдите боковую сторону равнобедренного треугольника, если его основание равно 16, а угол при основании равен 30°.
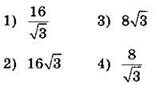
Часть 2
Запишите ответ к заданиям 4 и 5.
4°. К окружности с центром О и радиусом 12 см проведена касательная ВС (В — точка касания). Найдите длину отрезка ВС, если ОС = 13 см.
5. На рисунке точки Р и Н — середины сторон, СК — высота треугольника. Найдите площадь треугольника, если PH = 7 см, СК = 12 см.
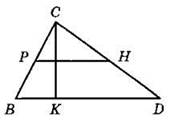
Часть 3
Запишите обоснованное решение задач 6 и 7.
6. В треугольнике MNK на стороне MN отмечена точка В, на стороне NK — точка С, причем ВС || МК. Найдите длину стороны МК, если сторона MN равна 12 см, ВМ = 4 см, ВС = 6 см.
7. В ромбе ABCD диагональ АС пересекает высоту ВН, проведенную к стороне AD, в точке К. Найдите длины отрезков ВК и КН, если сторона ромба равна 20 см, а высота равна 12 см.
ВАРИАНТ 2
Часть 1
Запишите номера верных ответов к заданиям 1—3.
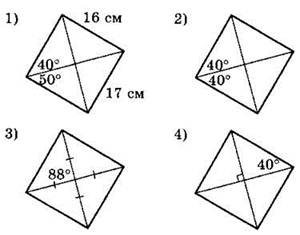
1°. На каждом из приведенных ниже рисунков изображен параллелограмм, обладающий теми или иными свойствами. Используя данные, приведенные на рисунках, укажите номера тех рисунков, на которых изображен прямоугольник.
2°. Используя данные, указанные на рисунке, найдите площадь изображенной ниже равнобедренной трапеции.
1) 52
2) 104
3) 80
4) 160

3°. Найдите высоту, проведенную к основанию равнобедренного треугольника, если основание равно 12, а угол при основании равен 30°.
![]()
Часть 2
Запишите ответ к заданиям 4 и 5.
4°. К окружности с центром О и радиусом 9 см проведена касательная CD (С — точка касания). Найдите длину отрезка OD, если CD = 12 см.
5. На рисунке точки М и К — середины сторон, DH — высота треугольника. Найдите площадь треугольника, если МК = 13 см, DH = 9 см.
Часть 3
Запишите обоснованное решение задач 6 и 7.
6. В прямоугольном треугольнике МОК из точки В гипотенузы МК проведен перпендикуляр BD к стороне МО. Найдите длину катета ОК, если BD = 6 см, МК = 21 см, ВК = 12 см.
7. В квадрате ABCD диагональ АС пересекает отрезок ВМ (М е AD) в точке Р. Найдите длины отрезков ВР и РМ, если сторона квадрата равна 16 см, а отрезок AM равен 12 см.
ВАРИАНТ 3
Часть 1
Запишите номера верных ответов к заданиям 1—3.
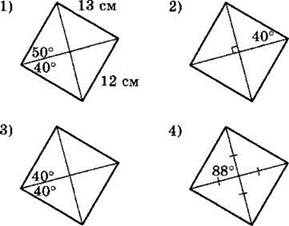
1°. На каждом из приведенных ниже рисунков изображен параллелограмм, обладающий теми или иными свойствами. Используя данные, приведенные на рисунках, укажите номера тех рисунков, на которых изображен ромб.
2°. Используя данные, указанные на рисунке, найдите площадь изображенной ниже равнобедренной трапеции.
1) 110
2) 55
3) 90
4) 180

3°. Найдите боковую сторону равнобедренного треугольника, если его основание равно 20, а угол при основании равен 30°.
![]()
Часть 2
Запишите ответ к заданиям 4 и 5.
4°. К окружности с центром О и радиусом 12 см проведена касательная МК (М — точка касания). Найдите длину отрезка МК, если ОК = 15 см.
5. На рисунке точки А и В — середины сторон, СН — высота треугольника. Найдите площадь треугольника, если АВ = 8 см, СН = 12 см.

Часть 3
Запишите обоснованное решение задач 6 и 7.
6. В треугольнике МРК на стороне МК отмечена точка А, на стороне РК — точка С, причем АС || МР. Найдите длину отрезка АС, если МК = 20 см, AM = 8 см, МР = 15 см.
7. В ромбе ABCD диагональ АС пересекает высоту DM, проведенную к стороне ВС, в точке Р. Найдите длины отрезков МР и DP, если сторона ромба равна 15 см, а высота равна 12 см.
ВАРИАНТ 4
Часть 1
Запишите номера верных ответов к заданиям 1—3.
1°. На каждом из приведенных ниже рисунков изображен параллелограмм, обладающий теми или иными свойствами. Используя данные, приведенные на рисунках, укажите номера тех рисунков, на которых изображен прямоугольник.
2°. Используя данные, указанные на рисунке, найдите площадь изображенной ниже равнобедренной трапеции.
1) 80
2) 40
3) 120
4) 60
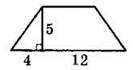
3°. Найдите высоту, проведенную к основанию равнобедренного треугольника, если основание равно 16, а угол при основании равен 30°.
![]()
Часть 2
Запишите ответ к заданиям 4 и 5.
4°. К окружности с центром О и радиусом 12 см проведена касательная DE (D — точка касания). Найдите длину отрезка ОЕ, если DE = 16 см.
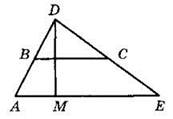
5. На рисунке точки B и С — середины сторон, DM — высота треугольника. Найдите площадь треугольника, если ВС = 13 см, DM = 7 см.
Часть 3
Запишите обоснованное решение задач 6 и 7.
6. В прямоугольном треугольнике BCD из точки М гипотенузы ВС проведен перпендикуляр МН к стороне BD. Найдите длину отрезка МН, если ВС = 24 см, МС = 9 см, CD = 16 см.
7. В квадрате ABCD диагональ BD пересекает отрезок АК (К ∈ ВС) в точке О. Найдите длины отрезков АО и ОК, если сторона квадрата равна 12 см, а отрезок ВК равен 9 см.