Дидактические материалы по геометрии 8 класс к учебнику Л. С. Атанасяна Геометрия 7-9 классы - 2017 год
ЧЕТЫРЕХУГОЛЬНИКИ - ОБУЧАЮЩИЕ РАБОТЫ
ОБУЧАЮЩАЯ РАБОТА № 1. Определение параллелограмма. Признаки параллелограмма
ВАРИАНТ 1
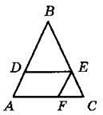
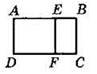
1. Дан ΔАВС (см. рисунок). Параллельно сторонам АВ и АС проведены прямые EF и DE. Определите вид четырехугольника ADEF.
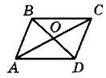
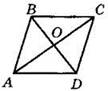
2. Дано: АО — медиана ΔABD, ВО — медиана ΔАВС (см. рисунок). Докажите, что ABCD — параллелограмм.
ВАРИАНТ 2
1. Прямая EF параллельна стороне АВ параллелограмма ABCD (см. рисунок). Докажите, что ABEF — параллелограмм.

2. В ΔАВС проведена медиана ВМ. На ее продолжении за точку М отложен отрезок MD, равный ВМ. Докажите, что четырехугольник ABCD является параллелограммом.
ВАРИАНТ 3
1. В параллелограмме ABCD проведена диагональ BD. Докажите, что ∠ABD = ∠CDB.
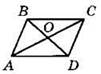
2. Дано: АС = 6 см, BD = 8 см, АО = 3 см, OD = 4 см (см. рисунок). Определите вид четырехугольника ABCD.
ВАРИАНТ 4
1. Дан параллелограмм ABCD, его диагонали пересекаются в точке О. Докажите, что ΔAOD = ΔСОВ.
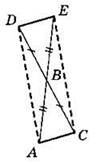
2. Стороны АВ и ВС треугольника АВС продолжены за точку В (см. рисунок), BD = ВС, BE = АВ. Докажите, что четырехугольник ADEC — параллелограмм.
ОБУЧАЮЩАЯ РАБОТА № 2. Свойства параллелограмма
ВАРИАНТ 1
1. ABCD — параллелограмм, ∠ACB = 30°, ∠BAC = 40°. Найдите ∠ADC.
2. Одна из сторон параллелограмма на 12 см больше другой. Периметр параллелограмма равен 56 см. Найдите стороны параллелограмма.
ВАРИАНТ 2
1. В параллелограмме МРКС диагональ PC перпендикулярна стороне МС и равна ей. Найдите углы параллелограмма.
2. Периметр параллелограмма равен 60 см. Найдите длины сторон, если известно, что диагональ параллелограмма делит угол на части 30° и 90°.
ВАРИАНТ 3
1. В параллелограмме МРКС из вершины тупого угла Р проведена высота PH к стороне МС так, что МН = HP. Найдите углы параллелограмма.
2. Найдите длины высот параллелограмма, если известно, что стороны равны 10 см и 12 см, а углы относятся как 5 : 1.
ВАРИАНТ 4
1. Найдите углы параллелограмма, если известно, что один из них в 8 раз меньше суммы всех остальных углов параллелограмма.
2. В треугольнике АВС на продолжении медианы ВМ за точку М отложен отрезок МН = ВМ. Найдите периметр четырехугольника АВСН, если периметр треугольника АВС равен 42 см, AM = 7 см.
ОБУЧАЮЩАЯ РАБОТА № 3. Биссектриса угла параллелограмма
ВАРИАНТ 1
1. Биссектриса угла параллелограмма пересекает его сторону, образуя с ней угол 48°. Найдите углы параллелограмма.
2. Биссектриса угла М параллелограмма МРКС пересекает сторону РК в точке В. Найдите периметр параллелограмма, если МР = 14, ВК = 15 см.
ВАРИАНТ 2
1. Биссектриса угла параллелограмма пересекает его сторону, образуя с ней угол 35°. Найдите углы параллелограмма.
2. Периметр параллелограмма ABCD равен 36 см. Биссектрисы углов BAD и CDA пересекаются на стороне ВС. Найдите длины сторон параллелограмма.
ВАРИАНТ 3
1. Биссектриса угла А параллелограмма АВС К пересекает сторону ВС в точке М. Найдите углы параллелограмма, если известно, что ∠AMC = 138°.
2. Периметр параллелограмма ABCD равен 40 см. Биссектриса АК угла BAD и биссектриса DM угла CDA делят сторону ВС на три равные части так, что точка К лежит между точками В и М. Найдите длины сторон параллелограмма.
ВАРИАНТ 4
1. Биссектриса угла К параллелограмма АВСК пересекает сторону ВС в точке М. Найдите углы параллелограмма, если известно, что ∠BMK = 146°.
2. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в ее середине М. Периметр треугольника АВМ равен 16 см, а длина отрезка AM больше стороны АВ на 1 см. Найдите периметр параллелограмма.
ОБУЧАЮЩАЯ РАБОТА № 4. Трапеция
ВАРИАНТ 1
1. В равнобедренной трапеции высота, проведенная из вершины тупого угла, делит большее основание на отрезки 5 см и 15 см. Найдите основания трапеции.
2*. Два противоположных угла равнобедренной трапеции относятся как 2 : 7. Найдите углы трапеции.
ВАРИАНТ 2
1. В равнобедренной трапеции диагональ является биссектрисой острого угла. Периметр трапеции равен 14 см, а большее основание — 5 см. Найдите меньшее основание.
2*. В равнобедренной трапеции диагональ перпендикулярна боковой стороне. Найдите углы трапеции, если известно, что боковая сторона в два раза меньше большего основания.
ВАРИАНТ 3
1. В равнобедренной трапеции сумма оснований равна сумме боковых сторон, периметр равен 32 см. Найдите боковую сторону трапеции.
2*. Могут ли углы трапеции МКРН быть пропорциональны числам 5 : 13 : 11 : 7?
ВАРИАНТ 4
1. В равнобедренной трапеции АВСМ (AM - большее основание) диагональ АС - биссектриса угла А. Найдите углы трапеции, если ∠ACM = 81°.
2*. Равнобедренную трапецию диагональ разбила на два треугольника, разность периметров которых равна 12 см, а сумма оснований равна 36 см. Найдите основания трапеции.
ОБУЧАЮЩАЯ РАБОТА № 5. Прямоугольник
ВАРИАНТ 1
1. В прямоугольнике ABCD проведена диагональ АС. Известно, что ∠ВАС в 2 раза больше, чем ∠АСВ. Чему равны эти углы?
2. Одна из сторон прямоугольника на 3 см больше другой. Найдите стороны прямоугольника, если его периметр равен 18 см.
ВАРИАНТ 2
1. Меньшая сторона прямоугольника равна 5 см, угол между диагоналями равен 60°. Найдите диагонали прямоугольника.
2. Дан прямоугольник ABCD, О — точка пересечения его диагоналей. Докажите, что ΔВОС и ΔAOD — равные равнобедренные треугольники.
ВАРИАНТ 3
1. Найдите диагонали прямоугольника, если его периметр равен 98 см, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 90 см.
2. Докажите, что отрезок, соединяющий точку пересечения диагоналей прямоугольника с серединой стороны, перпендикулярен этой стороне.
ВАРИАНТ 4
1. В прямоугольнике МРКС диагональ PC в 8 раз больше стороны МР. Периметр треугольника МОР равен 45 см (О - точка пересечения диагоналей). Найдите длину диагонали МК.
2. Из точки Е, взятой на стороне ВА прямоугольника ABCD, опущен перпендикуляр EF на сторону CD. Докажите, что четырехугольник AEFD — прямоугольник.
ОБУЧАЮЩАЯ РАБОТА № 6. Свойства ромба. Свойства квадрата
ВАРИАНТ 1
1. Один из углов ромба равен 70°. Определите остальные углы.
2. В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 5. Найдите периметр этого квадрата.
ВАРИАНТ 2
1. В ромбе ABCD проведена диагональ АС, Определите вид треугольника АВС и найдите его углы, если ∠ADC = 130°.
2. В окружности проведены два взаимно перпендикулярных диаметра АС и BD. Определите вид четырехугольника ABCD.
ВАРИАНТ 3
1. В ромбе ABCD ∠ABC = 140°. Найдите углы треугольника АОВ (О — точка пересечения диагоналей).
2. В квадрате ABCD проведена диагональ АС. Определите вид треугольника ACD и найдите все его углы.
ВАРИАНТ 4
1. Диагонали квадрата ABCD пересекаются в точке О. Определите вид треугольника AOD и найдите все его углы.
2. Две окружности с центрами в точках O1 и О2 и равными радиусами пересекаются в точках А и В (см. рисунок). Определите вид четырехугольника O1AO2B.
