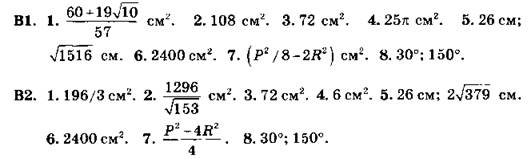Контрольные и самостоятельные работы по алгебре и геометрии 9 класс - 2016 год
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ - Урок 3 - ГЕОМЕТРИЯ - ОТВЕТЫ
(по учебнику А.В. Погорелова)
С1
В1. 1. 44°.
2. х = 6, у = 2,5.
3. Доказательство: Пусть ΔА1В1С1 и ΔА2В2С2 подобны. Тогда ![]() Пусть ΔА1В1С1 — равнобедренный. Тогда две его стороны равны. Пусть это будут стороны а1, b1. То есть а1 = b1. (В противном случае стороны можно переобозначить.) Тогда из равенств
Пусть ΔА1В1С1 — равнобедренный. Тогда две его стороны равны. Пусть это будут стороны а1, b1. То есть а1 = b1. (В противном случае стороны можно переобозначить.) Тогда из равенств ![]() Это значит, что второй треугольник также равнобедренный. Что и требовалось доказать.
Это значит, что второй треугольник также равнобедренный. Что и требовалось доказать.
В2. 1. 40°.
2. х = 3, у = 4.
3. Доказательство: Пусть ΔА1В1С1 и ΔА2В2С2 подобны. Тогда ![]() Пусть ΔА1В1С1 — равносторонний. Тогда все его стороны равны. То есть а1 = b1 = с1. Тогда из равенств
Пусть ΔА1В1С1 — равносторонний. Тогда все его стороны равны. То есть а1 = b1 = с1. Тогда из равенств ![]() следует а2 = b2 = с2 . Это значит, что второй треугольник также равносторонний. Что и требовалось доказать.
следует а2 = b2 = с2 . Это значит, что второй треугольник также равносторонний. Что и требовалось доказать.
В3. 1. ∠A = 60°; ∠B = 60°; ∠C = 100° ; ∠D = 140°.
2. 12 см; 16 см.
3. Доказательство: Из подобия треугольников следует ![]() — коэффициент подобия. Если
— коэффициент подобия. Если ![]() то
то ![]()
![]() Нарушается неравенство треугольника, которое должно быть верным. Получено противоречие. Отсюда
Нарушается неравенство треугольника, которое должно быть верным. Получено противоречие. Отсюда ![]() Что и требовалось доказать.
Что и требовалось доказать.
В4. 1. ∠А = 130°; ∠B = 50°; ∠C = 70°; ∠D = 110°
2. 5 см; 5 см; 6 см.
3. Доказательство:
Из подобия треугольников следует ![]() k — коэффициент подобия. Если
k — коэффициент подобия. Если ![]() то
то ![]()
![]() То есть b + c < d. Но, по неравенству треугольника, должно быть b + c > d. Получено противоречие. Отсюда
То есть b + c < d. Но, по неравенству треугольника, должно быть b + c > d. Получено противоречие. Отсюда ![]() Что и требовалось доказать.
Что и требовалось доказать.
С2
B1. 1. Доказательство: ∠AOB = ∠COD как вертикальные. ∠B = ∠D, значит, треугольники подобны по двум углам. Что и требовалось доказать.
2. Доказательство: По теореме Пифагора 82 + B1C12 = 102. Отсюда ![]() ∠A = ∠A1, так как оба угла острые. Треугольники — прямоугольные. Следовательно, треугольники подобны по двум углам. Что и требовалось доказать.
∠A = ∠A1, так как оба угла острые. Треугольники — прямоугольные. Следовательно, треугольники подобны по двум углам. Что и требовалось доказать.
3. Доказательство: ![]() Значит, две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны. По признаку подобия треугольников — по двум сторонам и углу между ними — треугольники подобны. У этих подобных треугольников В соответствует Е, А соответствует D. Действительно, угол между сторонами ВА и ВС — это ∠B, а угол между сторонами ED и EF — это ∠E. У подобных треугольников соответствующие углы равны. Поэтому ∠А = ∠D. Что и требовалось доказать.
Значит, две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны. По признаку подобия треугольников — по двум сторонам и углу между ними — треугольники подобны. У этих подобных треугольников В соответствует Е, А соответствует D. Действительно, угол между сторонами ВА и ВС — это ∠B, а угол между сторонами ED и EF — это ∠E. У подобных треугольников соответствующие углы равны. Поэтому ∠А = ∠D. Что и требовалось доказать.
В2. 1.Доказательство: ∠AOB = ∠COD как вертикальные. (Вертикальными углами, при пересечении двух прямых, называются пары противоположных углов, образованные при пересечении этих прямых.) ∠A = ∠D — по условию. Значит, треугольники подобны по двум углам. Что и требовалось доказать.
2. Ответ: Да. Доказательство: По теореме Пифагора 52 + А1В12 = 132. Отсюда ![]() Углы В, В1 — острые. Поэтому ∠B = ∠B1. Но ∠A = ∠A1 = 90°. Следовательно, треугольники подобны по двум углам. Что и требовалось доказать.
Углы В, В1 — острые. Поэтому ∠B = ∠B1. Но ∠A = ∠A1 = 90°. Следовательно, треугольники подобны по двум углам. Что и требовалось доказать.
3. ![]() То есть две стороны одного треугольника пропорциональны двум сторонам другого треугольника. По условию ∠BAC = ∠NMK. Следовательно, треугольники подобны по двум сторонам и углу между ними. ВС соответствует NK, АС соответствует МК. Поэтому угол С соответствует углу К. ∠C = ∠K. Что и требовалось доказать.
То есть две стороны одного треугольника пропорциональны двум сторонам другого треугольника. По условию ∠BAC = ∠NMK. Следовательно, треугольники подобны по двум сторонам и углу между ними. ВС соответствует NK, АС соответствует МК. Поэтому угол С соответствует углу К. ∠C = ∠K. Что и требовалось доказать.
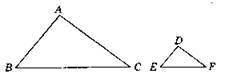
В3. 1. Доказательство: Треугольники ABD и ВЕС — прямоугольные и имеют общий угол В. Поэтому эти треугольники подобны по двум углам. Значит ![]() По двум сторонам и углу между ними треугольники BED и АВС подобны. Что и требовалось доказать.
По двум сторонам и углу между ними треугольники BED и АВС подобны. Что и требовалось доказать.
2. ![]() Отсюда
Отсюда ![]() Что и требовалось доказать.
Что и требовалось доказать.
3. Доказательство: Два многоугольника по определению подобны, если соответствующие стороны пропорциональны, а соответствующие в утлы равны. По условию ![]() так как трапеции прямоугольные. ∠D = ∠D1, так как острые углы равны. Поэтому
так как трапеции прямоугольные. ∠D = ∠D1, так как острые углы равны. Поэтому ![]() как половины равных углов. Прямоугольные треугольники ABD и A1B1D1 подобны по двум углам. ∠CBD = ∠ADB как внутренние накрест лежащие при параллельных прямых AD, ВС. Аналогично ∠C1B1D1 = ∠A1D1E1 как внутренние накрест лежащие при параллельных прямых А1D1, B1C1. Поэтому треугольники BCD и B1C1D1 — равнобедренные и подобные по двум углам. Из подобия соответствующих треугольников следует
как половины равных углов. Прямоугольные треугольники ABD и A1B1D1 подобны по двум углам. ∠CBD = ∠ADB как внутренние накрест лежащие при параллельных прямых AD, ВС. Аналогично ∠C1B1D1 = ∠A1D1E1 как внутренние накрест лежащие при параллельных прямых А1D1, B1C1. Поэтому треугольники BCD и B1C1D1 — равнобедренные и подобные по двум углам. Из подобия соответствующих треугольников следует ![]()
![]() Отсюда
Отсюда ![]() То есть соответствующие стороны пропорциональны. Значит, по определению подобия многоугольников, трапеции подобны. Что и требовалось доказать.
То есть соответствующие стороны пропорциональны. Значит, по определению подобия многоугольников, трапеции подобны. Что и требовалось доказать.
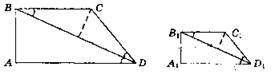
В4. 1. Доказательство: Треугольники ABD и ВЕС — прямоугольные и имеют равные углы с вершиной В как вертикальные. Поэтому эти треугольники подобны по двум углам. Сходственные стороны подобных треугольников пропорциональны, поэтому ![]() Отсюда
Отсюда ![]() ∠DBE = ∠ABC как вертикальные. Треугольники АВС и DBE подобны по двум сторонам и углу между ними. Что и требовалось доказать.
∠DBE = ∠ABC как вертикальные. Треугольники АВС и DBE подобны по двум сторонам и углу между ними. Что и требовалось доказать.
2. Доказательство: ![]() Поэтому-
Поэтому- ![]() По трем сторонам треугольники ACD и АВС подобны. Отсюда
По трем сторонам треугольники ACD и АВС подобны. Отсюда ![]() Что и требовалось доказать.
Что и требовалось доказать.
3. Доказательство: Два многоугольника подобны, если соответствующие стороны пропорциональны, а соответствующие углы равны. По условию ![]() так как трапеции прямоугольные. ∠C = ∠C1, так как тупые углы равны.
так как трапеции прямоугольные. ∠C = ∠C1, так как тупые углы равны. ![]() так как АС — биссектриса угла С. ∠B1C1A1 = ∠A1C1D1, так как диагональ А1С1 — биссектриса тупого угла. ∠BCA = ∠CAD как внутренние накрест лежащие при параллельных прямых ВС и AD. ΔАВС и ΔА1B1C1 подобны по двум углам. ∠ACB = ∠CAD как внутренние накрест лежащие при параллельных прямых AD, ВС. Аналогично ∠B1C1A1 = ∠C1A1D1 как внутренние накрест лежащие при параллельных Прямых A1D1, B1C1. Поэтому равнобедренные треугольники ACD и A1C1D1 — подобны по двум углам. Из подобия соответствующих треугольников следует
так как АС — биссектриса угла С. ∠B1C1A1 = ∠A1C1D1, так как диагональ А1С1 — биссектриса тупого угла. ∠BCA = ∠CAD как внутренние накрест лежащие при параллельных прямых ВС и AD. ΔАВС и ΔА1B1C1 подобны по двум углам. ∠ACB = ∠CAD как внутренние накрест лежащие при параллельных прямых AD, ВС. Аналогично ∠B1C1A1 = ∠C1A1D1 как внутренние накрест лежащие при параллельных Прямых A1D1, B1C1. Поэтому равнобедренные треугольники ACD и A1C1D1 — подобны по двум углам. Из подобия соответствующих треугольников следует ![]() Отсюда
Отсюда ![]() То есть соответствующие стороны трапеций пропорциональны. Так как соответствующие углы у двух трапеций равны, то, по определению подобия многоугольников, трапеции подобны. Что и требовалось доказать.
То есть соответствующие стороны трапеций пропорциональны. Так как соответствующие углы у двух трапеций равны, то, по определению подобия многоугольников, трапеции подобны. Что и требовалось доказать.

С3
В1. 1. В треугольнике A1B1C1 ∠B1 = 180° - 140° = 40°. ∠A1 = 90° - 40° = 50° = ∠А. Треугольники АВС и A1B1C1 прямоугольные. Следовательно, они подобны по двум углам. Что и требовалось доказать.
2. 60/13 см.
3. 64 см.
В2. 1. Доказательство: ∠A1B1C1 = ∠39° как вертикальные углы. В треугольнике A1B1C1 ∠A1 = 90° - 39° - 51° = ∠A. Треугольники ABC и A1B1C1 прямоугольные. Следовательно, они подобны по двум углам. Что и требовалось доказать.
2. 4 см.
3. 64 см.
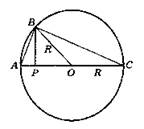
В3. 1. Прямоугольные треугольники АОВ1, ACA1, ОА1В, ВСB1 подобны между собой. Доказательство: Прямоугольные треугольники ОАB1, A1АС имеют общий острый угол А. Поэтому они подобны по двум углам. Прямоугольные треугольники A1OB, АОВ1 имеют общий острый угол О. Поэтому они подобны по двум углам. Прямоугольные треугольники А1CА, ВСВ1 имеют общий острый угол С. Поэтому они подобны по двум углам. Что и требовалось доказать.
2. 60 см.
3. 48 см.
В4. 1. Прямоугольные треугольники АОВ1, B1BC, ВA1О, АА1C подобны между собой. Доказательство: В прямоугольных треугольниках OBA1, B1BC угол при вершине В общий. По двум углам они подобны. В прямоугольных треугольниках ОВА1, АОВ1 углы АОB1, BOA1 равны как вертикальные. По двум углам треугольники ОВA1, AOB1 подобны. В прямоугольных треугольниках AOB1, АА1Cугол при вершине А общий. По двум углам они подобны. Что и требовалось доказать.
2. 15 см.
3. 84 см.
С4 (дом.)
В1. 1. 6 см, 15 см и 5 см, 2 см.
2. 42 см.
3. 14 см.
4. Доказательство: Так как отношения двух сторон треугольников равны, то пусть ![]() Пусть угол между биссектрисами, проведенными к стороне АВ, равен φ. Тогда угол между биссектрисами, проведенными к стороне A1B1, тоже равен φ.
Пусть угол между биссектрисами, проведенными к стороне АВ, равен φ. Тогда угол между биссектрисами, проведенными к стороне A1B1, тоже равен φ. ![]() ∠B + ∠C = ∠B1 + ∠C1. Отсюда ∠A = ∠A1. Треугольники ABC и A1B1C1 подобны по двум сторонам и углу между ними. Что и требовалось доказать.
∠B + ∠C = ∠B1 + ∠C1. Отсюда ∠A = ∠A1. Треугольники ABC и A1B1C1 подобны по двум сторонам и углу между ними. Что и требовалось доказать.
5. 4:1, считая от вершины А.
В2. 1. 7 см, 10 см и 14 см, 20 см.
2. 6√2 см.
3. 18 см.
4. Доказательство: Пусть в треугольнике АВС СМ — медиана, СН — высота, а в треугольнике А1В1С1 С1М1 — медиана, C1H1 — высота. Тогда, по условию, ∠HCM = ∠H1C1M1 = а. Так как М, М1 — центры описанных окружностей, то СМ = MB, C1M1 = M1B1, треугольники СМВ, С1М1В1 — равнобедренные. Так как внешний угол треугольника равен сумме внутренних углов, не смежных с ним, а сумма острых углов прямоугольного треугольника равна 90°, то 21B + а = 90° = 21B1 + а. Отсюда ∠B = ∠B1. Прямоугольные треугольники АВС и А1В1С1 подобны по двум углам. Что и требовалось доказать.
5. 1:1.
В1. 1. 110°. 2. 5 см. 3. 16 см.
В2. 1. 140°. 2. 24 см; 32 см. 3.12 см; 5 см.
В3. 1. 51°. 2. 25 см. 3. 9 см; 7 см.
В4. 1. 35°. 2. 25 см. 3. 2√62 см.
*С6
B1. 1. а) 1:7:10; б) 40°, 55°, 85°.
2. 140°, 90°, 40°, 90°.
3. Доказательство: Центральный угол в два раза больше соответствующего вписанного угла, опирающегося на ту же хорду. Поэтому ∠AOD = ∠DOC = 2β. Если центральные углы равны, то равны и соответствующие хорды, Значит, AD = DC. Треугольник ADC — равнобедренный. Что и требовалось доказать.

4. Пусть m — медиана, h — высота. АС — диаметр окружности радиуса m. Из точки А проводим перпендикуляр АР = h. Из точки Р проводим перпендикуляр до пересечения с окружностью в точке В. Соединяем А с В, В с С. Треугольник АВС — искомый.
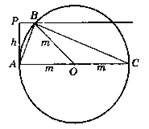
5. 240 см.
6. 40°; 140°.
7. 14 см.
8. 7,5 см.
В2. 1. а) 140°; 100°; 120°; б) 55°, 65°, 60°.
2. 140°, 105°, 40°, 75°.
3. Доказательство: Центральный угол в два раза больше соответствующего вписанного угла, опирающегося на ту же хорду. Поэтому ∠AOB = ∠BOC = 2β. Если центральные углы равны, то равны и соответствующие хорды. Значит, АВ = ВС. Треугольник АВС — равнобедренный. Что и требовалось доказать.
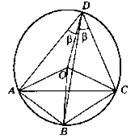
4. Пусть q — проекция катета АВ на гипотенузу АС. АС = с — диаметр окружности радиуса R = c/2. Из точки А проводим дугу окружности радиуса q до пересечения с диаметром АС в точке Р. Из точки Р проводим перпендикуляр до пересечения с окружностью в точке В. Соединяем А с В, В с С. Треугольник АВС — искомый.
5. 60 см.
6. 40°.
7. 24 см; 40см.
8. 2 см.
С7
В1. 1. 36 см. 2. 120°. 3. 3,5 см; 4,5 см.
В2. 1. 30 см. 2. 60°. 3. 4 см; 7 см.
В3. 1. √21 см; √61 см. 2. 120°. 3. 48 см.
В4. 1. √57 см; √73 см. 2. 120°. 3. 60 см.
С8
B1. 1. √2.
2. ВС, так как ∠A = 100° — тупой, значит — больший, а против большего угла лежит большая сторона.
3. 8 см.
В2. 1. 45°; 135°.
2. ВС, так как ∠В = 70°, ∠C = 75° и, значит, ∠A = 35° — наименьший, а против меньшего угла лежит меньшая сторона.
3. 20 см.
С9 (дом.)
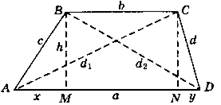
В1. 1. 120°.
2. 21/11 см; 56/11 см.
3. Доказательство: Из вершины С меньшего основания проведем перпендикуляр на большее основание и диагональ трапеции. Применим теорему Пифагора к двум образовавшимся прямоугольным треугольникам. Имеем: ![]()
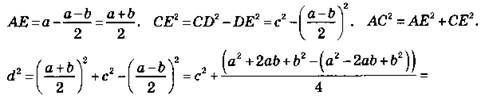
![]() Что и требовалось доказать.
Что и требовалось доказать.
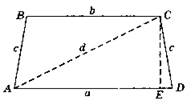
4. Решение: По теореме косинусов в треугольнике АВС:
![]()
![]() По теореме синусов в треугольнике АОВ:
По теореме синусов в треугольнике АОВ: ![]() Отсюда RAOB = 2 см. Ответ: 2 см.
Отсюда RAOB = 2 см. Ответ: 2 см.
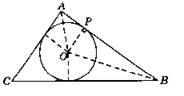
5. Доказательство: Из теоремы синусов ![]()
![]() Достаточно показать, что
Достаточно показать, что ![]() Имеем ∠AHB = ∠AHK + ∠KHB.
Имеем ∠AHB = ∠AHK + ∠KHB.
∠KAH — общий острый угол прямоугольных треугольников ABM и АКН. Поэтому ∠AHK = ∠B. Аналогично, ∠KBH — общий острый угол прямоугольных треугольников ABN и КВН. Поэтому ∠KHB = ∠A. Отсюда ∠AHB = ∠AHK + ∠KHB = ∠B + ∠A = 180° - ∠C.
sin∠AHB = sin(180° - ∠C) = sin∠C . Что и требовалось доказать.
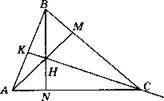
В2. 1. 60°.
2. 5,25 см; 8,75 см.
3. Доказательство: AN = а - у. MD = b + х. По теореме Пифагора имеем:
![]()
![]() Отсюда
Отсюда
![]()
![]()
Что и требовалось доказать.
4. Решение: ![]()
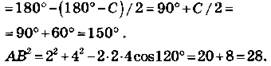
АВ = 2√7 см. По теореме синусов из треугольника АОВ имеем: ![]()
Отсюда RAOB = 2√7 см. Ответ: 2√7 см.
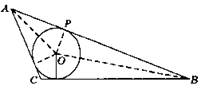
5. Указание. Покажите, что ∠AHC = ∠A + ∠C. С помощью теоремы синусов докажите, что эти радиусы равны радиусу окружности, описанной вокруг треугольника АВС. Из теоремы синусов следует
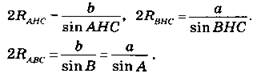
Достаточно показать, что sin AHC = sin B, sin BHC = sin A.
![]()
Поэтому ![]() Поэтому sin AHC = sin B. Аналогично получается
Поэтому sin AHC = sin B. Аналогично получается ![]() Поэтому sin ВНС = sin А. Что и требовалось доказать.
Поэтому sin ВНС = sin А. Что и требовалось доказать.

C10
B1. 1. 80°, 90°, 110°, 120°, 140°.
2. 7.
3. Доказательство: Если есть 4 тупых угла, то их сумма больше 360°, но сумма внутренних углов четырехугольника равна 360°. Противоречие. Значит, четырехугольник имеет не более трех тупых углов. Что и требовалось доказать.
В2. 1. 90°, 108°, 126°, 144°, 72°.
2. 7.
3. Доказательство: Сумма внешних углов многоугольника равна 360°. Если есть больше трех тупых углов среди них, то эта сумма больше 90° ∙ 4 = 360°. Противоречие. Что и требовалось доказать.
В3. 1. 50°, 160°, 150°, 50°, 160°, 150°.
2. 240°.
3. Нет. Доказательство: Если сумма шести углов девятиугольника меньше суммы трех оставшихся углов, которую обозначим X, то ![]()
![]() Тогда сумма трех углов
Тогда сумма трех углов ![]() Но сумма трех углов меньше, чем 180° ∙ 3. Противоречие. Что и требовалось доказать.
Но сумма трех углов меньше, чем 180° ∙ 3. Противоречие. Что и требовалось доказать.
В4. 1. 131°, 139°, 131°, 139°, 131°, 139°, 131°, 139°.
2. 230°.
3. Нет. Доказательство: Если сумма пяти углов восьмиугольника меньше суммы трех оставшихся углов, которую обозначим X, то ![]() Тогда сумма трех углов
Тогда сумма трех углов ![]() Но сумма трех углов меньше, чем 180° ∙ 3. Противоречие. Что и требовалось доказать.
Но сумма трех углов меньше, чем 180° ∙ 3. Противоречие. Что и требовалось доказать.
С11
B1. 1. 30.
2. 3 см, √3/2 см.
3. Доказательство: Отсекаем от правильного восьмиугольника 4 равнобедренных равных треугольника. Внутри остается четырехугольник из равных сторон — оснований равнобедренных равных треугольников. Так как вершины четырехугольника A1A3A5A7, то его диагонали равны A1A5 = A3A7, так как вершины A1, A5 — противоположные, и вершины A1, A5 — противоположные. Ромб с равными диагоналями — это квадрат. Что и требовалось доказать.
В2. 1. 45.
2. а) 8 см, б) 4√2 см.
3. Доказательство: Так как стороны нового семиугольника являются соответствующими средними линиями соответствующих равных (по первому признаку) треугольников, то все стороны нового семиугольника равны. Так как углы нового семиугольника получаются вычитанием от 180° двух одинаковых острых углов при основании равных треугольников, то все углы нового семиугольника равны.
В3. 1. 12; 15.
2. 1 + √3 см.
3. Доказательство: Диагонали пятиугольника равны как основания равных равнобедренных треугольников. ∠CBP = ∠CDQ = ∠BCP = ∠QCD = ∠QDC как углы при основаниях равных равнобедренных треугольников BCD, АРС, CDE. Треугольники ВСР и CDQ равнобедренные с равными основаниями и углами при них. Поэтому равны. PQ = BD - 2BQ = d - 2c = a1, где с — сторона звезды. Диагонали пятиугольника равны, стороны звезды равны. Поэтому все стороны внутреннего пятиугольника равны. Треугольники ВРТ, PCQ, QDR, RES, TAS равны по трем сторонам. ∠TPQ = 180° - ∠CPQ. Все углы внутреннего пятиугольника равны, так как ∠CPQ равен углу при основаниях перечисленных пяти равнобедренных треугольников. Все стороны и все углы пятиугольника равны. Поэтому он — правильный. Что и требовалось доказать.
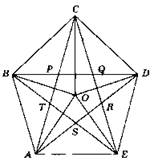
В4. 1. 45; 50.
2. 2 см.
3. Доказательство: ΔPCQ, ΔQDR — равнобедренные.
![]()
![]()
Все углы и все стороны равны. Пятиугольник правильный. Что и требовалось доказать.

С12
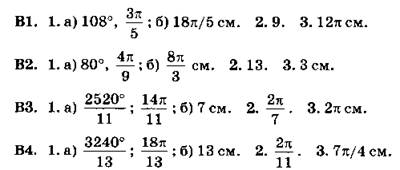
С13
В1. 1. 18 см2. 2. а) 225 см2; б) 15 см. 3. 36 см.
В2. 1. 252 см2. 2. а) 64 см2; б) 8 см. 3. 72 см.
В3. 1. 63 см2. 2. 37,5 см2. 3. 4 см; 49 см.
В4. 1. 30 см2. 2. 150 см2. 3. 15 см.
С14

С15
В1. 1. 65 см2. 2. 384 см2. 3. 2 см.
В2. 1. 100 см2. 2. 96 см2. 3. 4 см.
В3. 1. 340√21 см2. 2. 9,6 см. 3. 49 см2.
В4. 1. 45 см2. 2. 192 см2. 3. 400 см2.
С16 (дом.)
B1. 1. 85/3 см; 12 см. 2. 6,25 см. 3. 24 см. 4. 10 см. 5. 24 см. 6. 13π см. 7. 2 см. 8. 2,1см. 9. 12,5 см. 10. 9√3 см2.
В2. 1. 16,25 см; 8 см. 2. 50 см. 3. 25 см. 4. 2,5 см; 1 см. 5. 7,5 см. 6. 25π см. 7. 72 см. 8. 3 см. 9. 12,5 см. 10. 9√3 см2.
С17
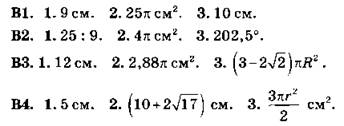
С18 (дом.)