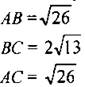ПРОСТЕЙШИЕ ЗАДАЧИ В КООРДИНАТАХ. РЕШЕНИЕ ЗАДАЧ - МЕТОД КООРДИНАТ

Цель деятельности учителя

Создать условия для закрепления знаний учащихся в ходе решения задач, обучения решению задач в координатах

Термины и понятия

Вектор, координаты вектора, метод координат, координаты середины отрезка, длина вектора, расстояние между точками

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют базовым понятийным аппаратом; умеют применять метод координат для решения задач

Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения, формулировать выводы.

Регулятивные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют контролировать процесс и результат учебной деятельности.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.

Личностные: проявляют познавательный интерес к изучению предмета

Организация пространства

Формы работы

Фронтальная (Ф); парная (П); индивидуальная (И)

Образовательные

ресурсы

Карточки для индивидуальной работы

I этап. Актуализация знаний учащихся

Цель деятельности

Совместная деятельность

Проверить уровень теоретических знаний по теме

(И/Ф)

1. Двое учащихся работают по карточкам у доски:

Карточка 1

1) Вывести формулы координат середины отрезка.

2) Решить задачу № 942.

Карточка 2

1) Вывести формулу расстояния между двумя точками.

2) Решить задачу № 937.

2. С остальными учащимися проводится устная работа по решению задач:

1) Найдите координаты вектора равного разности векторов если

2) Найдите координаты вектора равного сумме векторов если

3) Найдите координаты середины отрезка DK, если D (-6; 4), К (2; -8).

4) Найдите длину отрезка СР, если С(3; -2), Р (-5; 4).

5) Найдите длину вектора равного если

6) Найдите координаты вектора если вектора если

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач

(П)

1. Решить задачу № 947 (а).

2. Решить задачу № 946 (б).

(Ф/И)

3. Решить задачу № 948 (б) на доске и в тетрадях.

4. Решить задачу № 950 (б) на доске и в тетрадях.

5. Решить задачу № 951 (а)

№ 947 (а).

Решение:

Найдем длины сторон треугольника АВС по формуле расстояния между точками:

Так как АВ = АС, то по определению равнобедренного треугольника ∆ABC - равнобедренный. Найдем его площадь; проведем высоту AM ⊥ ВС: AM -

высота и медиана в равнобедренном треугольнике.

Пусть М(х; у), тогда х = 3, у = -1.

Значит, точка М(3; -1). Найдем длину АМ = √13.

S_ABC = 13.

Ответ: 13

III этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Какие формулы повторили на уроке?

- Оцените свою работу на уроке

(И) Домашнее задание: повторить материал пунктов 88 и 89; решить задачи № 947 (б), 949 (а), 951 (б), 953