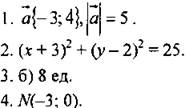КОНТРОЛЬНАЯ РАБОТА № 1 - МЕТОД КООРДИНАТ

Цель деятельности учителя

Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала

Термины и понятия

Метод координат, уравнение окружности, уравнение прямой, длина вектора, расстояние между точками, координаты середины отрезка

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности

Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям.

Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль.

Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве.

Личностные: осознают важность и необходимость знаний в жизни человека

Организация пространства

Формы работы

Индивидуальная (И); фронтальная (Ф)

Образовательные

ресурсы

• Задания для контрольной работы

I этап. Выполнение контрольной работы

Цель деятельности

Задание для контрольной работы

Осуществить проверку знаний, умений и навыков по изученному материалу

(И) Вариант I

1. Найдите координаты и длину вектора если

2. Напишите уравнение окружности с центром в точке A(-3; 2), проходящей через точку В(0; -2).

3. Треугольник MNK задан координатами своих вершин: М(-6; 1), N(2; 4), К(2; -2).

а) Докажите, что ∆MNK - равнобедренный.

б) Найдите высоту, проведенную из вершины М.

4*. Найдите координаты точки N, лежащей на оси абсцисс и равноудаленной от точек Р(-1; 3) и K(0; 2).

Вариант II

1. Найдите координаты и длину вектора если

2. Напишите уравнение окружности с центром в точке С(2; 1), проходящей через точку D(5; 5).

3. Треугольник CDE задан координатами своих вершин: С(2; 2), D(6; 5), Е(5; -2).

а) Докажите, что ∆CDE - равнобедренный.

б) Найдите биссектрису, проведенную из вершины С.

4*. Найдите координаты точки А, лежащей на оси ординат и равноудаленной от точек В(1; -3) и С(2; 0).

Ответы:

Вариант I

Вариант II

II этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Что выполняли на уроке?

- Как оцениваете свою деятельность на уроке?

- Какие задания вызвали затруднения? Почему?

(И) Домашнее задание: повторить материал пунктов 79-96; ответить на вопросы 1-8, с. 244