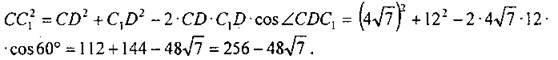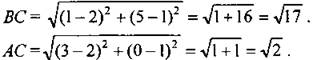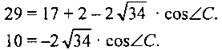Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
РЕШЕНИЕ ЗАДАЧ - Урок 3 - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
|
Цель деятельности учителя |
Создать условия для подготовки к контрольной работе; совершенствовать навыки решения задач на применение скалярного произведения векторов |
|||
|
Термины и понятия |
Косинус, угол между векторами, скалярное произведение, скалярный квадрат |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: понимают и используют математические средства наглядности для иллюстрации, интерпретации, аргументации; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий. Регулятивные: понимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: участвуют в диалоге. Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Задания для математического диктанта, домашнего задания |
|||
|
I этап. Активизация знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проверить выполнение домашнего задания, уровень владения теоретическими знаниями |
(Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. 1. Математический диктант: Вариант I 1. Вычислите скалярное произведение векторов 2. Скалярное произведение ненулевых векторов 3. Вычислите скалярное произведение векторов 4. Найдите угол между ненулевыми векторами 5. Вычислите косинус угла между векторами 6. Даны векторы Вариант II 1. Вычислите скалярное произведение векторов 2. Скалярное произведение ненулевых векторов 3. Вычислите скалярное произведение векторов 4. Найдите угол между ненулевыми векторами 5. Вычислите косинус угла между векторами 6. Даны векторы |
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать навыки решения задач |
(Ф/И) 1. Решить № 1049 (вместе с учителем). 2. Решить № 1051 и 1053 (самостоятельно, с взаимопроверкой). 3. Решить № 1065, 1070 |
№ 1049.
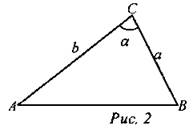
Дано: Найти: ∠А, ∠В, ∠C. Решение:
Ответ: 60°; ≈ 21°47'; ≈ 98°13'. № 1070. Дано: ∆ABCD - трапеция, AD = 16 см, BC = 8 cm, CD = 4√7 cm, ∠ADC = 60°; SABCC1 = SCC1D. Найти: SABCD, CC1. Решение (рис. 221): Из ∆CDH (∠H = 90°)
Тогда Из По теореме косинусов:
Тогда Ответ: № 1065.
Дано: A(3; 0), B(1; 5); C(2; 1). Доказать: ∆ABC – тупоугольный. Найти: cosα. Решение:
2) По теореме косинусов
Ответ: |
||
|
III этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) - Закончите фразы: • Чтобы найти косинус угла между векторами, надо... • Векторы перпендикулярны, если.... - Оцените свою работу на уроке |
(И) Домашнее задание. С-10*. Решение треугольников. Скалярное произведение (домашняя самостоятельная работа). (См. Ресурсный материал.) |
|||
Ресурсный материал
Домашняя самостоятельная работа
|
Вариант I |
Вариант II |
|
1. Дан равнобедренный треугольник. Найдите отношение радиусов вписанной исписанной окружностей, если: |
|
|
угол при вершине равен α. |
угол при основании равен β. |
|
2. Дан выпуклый четырехугольник. Отрезки, соединяющие середины противоположных сторон, равны а и b и пересекаются под углом 60°. Найдите диагонали четырехугольника. |
Дан выпуклый четырехугольник. Его диагонали равны с и d и пересекаются под углом 60°. Найдите отрезки, соединяющие середины противоположных сторон. |
|
3. Докажите, что углы треугольника АВС связаны соотношением:
|
|
|
4. Дан прямоугольник ABCD. Докажите, что для любой точки О выполняется равенство: |
|
|
|
|
|
5. Даны произвольные точки А, В, С и D. Докажите равенство: |
|
|
|
|

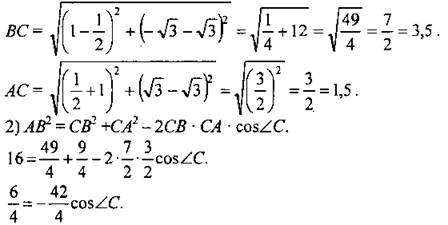
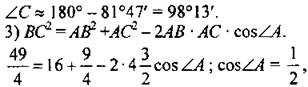 следовательно, ∠A = 60°.
следовательно, ∠A = 60°.