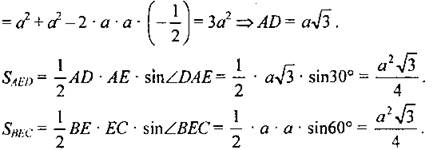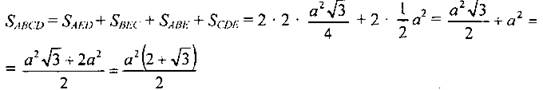Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ПОСТРОЕНИЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ - ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА
|
Цель деятельности учителя |
Создать условия для выработки у учащихся умения строить некоторые правильные многоугольники с помощью циркуля и линейки |
||||
|
Термины и понятия |
Правильный многоугольник, описанная и вписанная окружности |
||||
|
Планируемые результаты |
|||||
|
Предметные умения |
Универсальные учебные действия |
||||
|
Умеют строить некоторые правильные многоугольники |
Познавательные: понимают и используют математические средства наглядности для иллюстрации, интерпретации, аргументации. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач, контролировать процесс и результат учебной математической деятельности. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют познавательный интерес к изучению предмета |
||||
|
Организация пространства |
|||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||||
|
Образовательные ресурсы |
• Задания для индивидуальной работы |
||||
|
I этап. Актуализация опорных знаний учащихся |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
Выявить трудности, возникшие при выполнении домашнего задания |
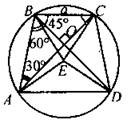
(Ф/И) 1. Проверить решение задач № 1087 и 1088. 2. Ответить на вопросы учащихся. 3. Организовать решение задачи: В трапеции ABCD меньшее основание ВС равно а, прилежащие к этому основанию углы равны 105°, диагонали взаимно перпендикулярны. Найти площадь трапеции |
Решение:
Опишем около данной трапеции окружность. Так как ∠BAD = 30° (см. I способ), то ∪BC= 60°, а значит центральный угол ВЕС = 60°, где Е - центр описанной окружности, отсюда ∆ВЕС - равносторонний, BE = ЕС = а и, соответственно, радиус описанной окружности равен а.
В ∆AED по теореме косинусов
Так как ∠BЕС = 60°, ∠AED = 120°, то ∠AEB = ∠CED = 90°, тогда
|
|||
|
II этап. Построение многоугольников |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Научить строить с помощью циркуля и линейки правильный треугольник, четырехугольник и шестиугольник |
(Ф) 1. Решение задачи 1 пункта 113 на с. 274. 2. Построение правильного треугольника, вписанного в окружность. 3. Решение задачи 2 пункта 113. 4. Построение правильного двенадцатиугольника, вписанного в окружность (рис. 310, с. 275). 5. Построение правильных четырехугольника, восьмиугольника, шестнадцатиугольника, вписанных в окружность. 6. Построение правильных шестиугольника, треугольника, описанных около окружности. 7. Построение правильных четырехугольника, восьмиугольника, описанных около окружности |
||||
|
III этап. Самостоятельная работа с взаимопроверкой |
|||||
|
Цель деятельности |
Задания для самостоятельной работы |
||||
|
Проверить уровень теоретических знаний и умение их применять при решении задач |
(И) Вариант I 1. Найдите углы правильного пятнадцатиугольника. 2. Сторона правильного треугольника, вписанного в некоторую окружность, равна 4√3. Найдите сторону правильного четырехугольника, описанного около этой же окружности. Вариант II 1. Найдите углы правильного восемнадцатиугольника. 2. Сторона правильного четырехугольника, вписанного в некоторую окружность, равна 2. Найдите сторону правильного треугольника, описанного около этой же окружности. Ответы: Вариант I: 1) 156°; 2) 8. Вариант II: 1) 160°; 2) 2√6 |
||||
|
IV этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
(Ф/И) - Что нового для себя открыли на уроке? - Оцените свою работу на уроке |
(И) Домашнее задание: решить № 1094, 1095, 1097, 1098 |
||||