Системы уравнений как математические модели реальных ситуаций - Системы уравнений

Цель: использовать системы уравнений для решения текстовых задач.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (тест).

Вариант 1

1. Способом подстановки решите систему уравнений

Ответы: а) (1; 2); б) (1; 2), (32; -13,5); в) (1; 2), г) (1; 2), (23;-9).

2. Способом сложения решите систему уравнений

Ответы: а) (0; -4), (4; -4); б) (4; -4); в) (2; -4); г) (4; -6).

Вариант 2

1. Способом подстановки решите систему уравнений

Ответы: а) (2; -1); б) (2; -1), в) (2; -1), (34; -65); г) (2; -1), (18; -33).

2. Способом сложения решите систему уравнений

Ответы: а) (-3; 1); б) (-3; 2); в) (-3; -3); г) (-3; 1), (-3; -3).

III. Изучение нового материала

Системы уравнений с двумя переменными часто используются при решении текстовых задач. Для этого применяют стандартную схему:

Первый этап - составление математической модели;

Второй этап - работа с составленной моделью;

Третий этап - ответ на вопрос задачи.

На примерах рассмотрим использование этой схемы.

Пример 1

Произведение двух чисел равно 168, а сумма их квадратов равна 340. Найдем эти числа.

Первый этап - составление математической модели.

Пусть одно из чисел равно х, другое - у. Тогда их произведение ху. По условию задачи оно равно 168. Получаем первое уравнение: ху = 168. Квадрат одного числа равен х², квадрат другого числа – у². Сумма квадратов чисел составляет х² + у². По условию такая сумма равна 340. Имеем второе уравнение: х² + у² = 340. Итак, для нахождения чисел х и у получили систему двух уравнений с двумя неизвестными: Таким образом, математическая модель задачи составлена.

Второй этап - работа с составленной моделью.

Каждое уравнение полученной системы имеет вторую степень. Поэтому система уравнений нелинейна. Для ее решения можно предложить два способа.

1-й способ. Используем способ подстановки. Из первого уравнения выразим и подставим во второе уравнение. Получаем: или х⁴ – 340x² + 28 224 = 0. Корни этого биквадратного уравнения x_1,2 = ±12 и x_3.4 = ±14. По формуле найдём соответствующие значения у: y_1,2 = ±14 и у_3,4 = ±12. Итак, задача имеет четыре решения: (12; 14), (-12; -14), (14; 12), (-14; -12).

2-й способ. Используем способ сложения. Умножим первое уравнение на 2 и запишем систему уравнений в виде Сложим и вычтем уравнения системы. Имеем: или или

Таким образом, данная система сводится к четырем системам линейных уравнений:

а) - решение(12; 14);

б) - решение (-12; -14);

в) - решение(14; 12);

г) - решение (-14; -12).

Третий этап - ответ на вопрос задачи.

По условию задачи не требуется конкретизировать, какое из чисел первое, а какое второе. Поэтому искомые числа 12 и 14, а также числа, противоположные им: -12 и -14.

Пример 2

Периметр прямоугольного треугольника равен 30 см, а его гипотенуза равна 13 см. Найдите стороны треугольника.

Первый этап - составление математической модели.

Пусть катеты треугольника равны х см и у см. Учтем, что периметр многоугольника - сумма длин всех его сторон. Получаем первое уравнение: х + у + 13 = 30 см. Для записи второго уравнения учтем теорему Пифагора: сумма квадратов катетов равна квадрату гипотенузы. Имеем второе уравнение: х² + у² = 13². Итак, для нахождения катетов треугольника получили систему уравнений:

Второй этап - работа с составленной моделью.

Запишем полученную систему уравнений в виде Первое уравнение системы линейное, второе уравнение имеет вторую степень. Поэтому решим эту систему способом подстановки. Из первого уравнения выразим у = 17 - х и подставим во второе уравнение. Получаем квадратное уравнение: х² + (17 - х)² = 169 или х² - 17х + 60 = 0, корни которого x₁ = 5 и х₂ = 12. По формуле у = 17 - х найдем соответствующие значения у: у₁ = 17 - 5 = 12 и у₂ = 17 - 12 = 5.

Третий этап - ответ на вопрос задачи.

Система уравнений имеет два решения: (5; 12) и (12; 5). Так как непонятно, какой из катетов первый, а какой второй, то запишем ответ: катеты треугольника равны 5 см и 12 см.

Пример 3

Катер проходит 80 км но течению реки и 40 км - против течения за 6 ч 30 мин. Тот же катер проходит 40 км по течению и 80 км - против течения за 7 ч. Найти собственную скорость катера и скорость течения реки.

Первый этап - составление математической модели.

Пусть х (км/ч) - собственная скорость катера, у (км/ч) - скорость течения реки. Тогда скорость катера по течению реки (х + у) (км/ч), против течения реки - (х -у) (км/ч).

80 км по течению реки катер проходит за время (ч), а 40 км против течения - за время (ч). Так как в этом случае на весь путь было затрачено 6 ч 30 мин (т. е. ч), то получаем первое уравнение:

Рассмотрим вторую ситуацию. 40 км по течению реки катер проходит за время (ч), 80 км против течения - за время (ч). В этом случае на весь путь было затрачено время 7 ч. Поэтому получаем второе уравнение:

Для нахождения собственной скорости катера х и скорости течения реки у имеем систему уравнений: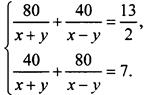

Второй этап - работа с составленной моделью.

Получили систему рациональных уравнений. Если в каждом уравнении избавиться от знаменателей, то увидим, что уравнения имеют вторую степень (т. е. нелинейны).

Учитывая структуру уравнений системы, решим ее способом введения новых переменных: Тогда исходная система уравнений становится линейной: 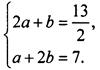Решим эту систему, например, способом алгебраического сложения. Умножим первое уравнение на (-2) и получим систему Сложим эти уравнения и получим: -3а = -6, откуда а = 2. Подставим такую величину во второе уравнение: 2 + 2b = 1, откуда b = 5/2. Вернемся к старым переменным. Имеем систему уравнени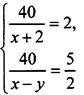й или Сложим и вычтем, соответственно, уравнения системы. Получаем: 2х = 36 (откуда х = 18) и 2у = 4 (откуда y = 2).

Третий этап - ответ на вопрос задачи.

Решив систему уравнений, получили: х = 18 и у = 2. Итак, собственная скорость катера 18 км/ч, скорость течения реки 2 км/ч.

Как видно из примеров 1-3, при решении получающихся систем уравнений использовались рассмотренные ранее методы. При этом трудностей не возникало (второй этап схемы решения). Практика показывает, что затруднение у школьников обычно возникает при составлении математической модели задачи (первый этап).

Пример 4

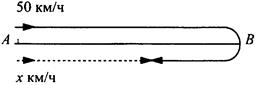
Из пункта А в пункт В, расстояние между которыми 70 км, выехал велосипедист, а через некоторое время - мотоциклист со скоростью 50 км/ч. Мотоциклист догнал велосипедиста в 20 км от пункта А. Прибыв в В, мотоциклист через 36 мин выехал обратно и встретился с велосипедистом спустя 3 ч 20 мин после выезда велосипедиста из А. Найти скорость велосипедиста.

Первый этап - составление математической модели.

Пусть х (км/ч) - скорость велосипедиста, t (ч) - время, через которое выехал из пункта А мотоциклист после велосипедиста. Опишем условия задачи. Раз мотоциклист выехал на t (ч) позже велосипедиста, то он и находился в пути на t (ч) меньше.

Первая встреча произошла в 20 км от А. Велосипедист проехал это расстояние за время 20/x (ч), мотоциклист - за время (ч). Учтем, что мотоциклист находился в пути на t (ч) меньше. Получаем первое уравнение:

Опишем вторую встречу. Она произошла через 3 ч 20 мин = (ч) после выезда велосипедиста из А. Он за это время проехал расстояние (км). Мотоциклист находился в пути (ч) (учтем, что 36 мин = ч). За это время он проехал (км). Из рисунка видно, что сумма расстояний, пройденных велосипедистом и мотоциклистом до второй встречи, равна удвоенному расстоянию между пунктами А и В. Получаем второе уравнение: Итак, получили систему уравнении: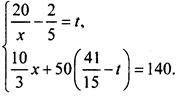

Заметим, что описание условий задачи (получение системы уравнений) может вызвать определенные трудности.

Второй этап - работа с составленной моделью.

Способ решения определяет условие задачи: надо найти скорость велосипедиста х. Поэтому подставим первое уравнение во второе и постепенно преобразуем полученное уравнение. Имеем: или или х² + 47х - 300 = 42х, или х² + 5х - 300 = 0. Корни этого квадратного уравнения х₁ = 15 и х₂ = -20.

Третий этап - ответ на вопрос задачи.

Очевидно, что ответ х = -20 смысла не имеет, так как скорость велосипедиста не может быть отрицательной. Тогда скорость велосипедиста 15 км/ч. Для интереса найдем время мин (т. е. мотоциклист выехал через 56 мин после велосипедиста).

IV. Задание на уроках

§ 7, № 1, 5, 12, 16, 18, 22, 29, 38, 44, 49, 54.

V. Задание на дом

§ 7, № 2, 8, 13, 17, 19, 23, 30, 39, 45, 50, 55.

VI. Подведение итогов уроков