Решения заданий работы - Государственная итоговая аттестация по алгебре (ГИА)

Часть 1

1. Число всех учащихся в школе примем за 100%, тогда число учащихся 10-11 классов в соответствии с диаграммой:

100 - 48 - 34 = 18%.

Ответ: 18%.

2. Переведем обыкновенные дроби в десятичные и оценим приведенные суммы:

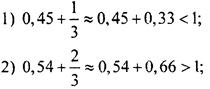
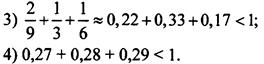
Видно, что только сумма 2) больше 1.

Ответ: 2.

3. Из приведенного рисунка видно, что a < 0 и b > 0. Поэтому легко оценить числа: 2a < a < 0, a < a + b < b и 2b > b > 0. Итак, наибольшее число 2b.

Ответ: 3.

4. Подставим в выражение величины и получим:

Ответ: 2/3.

5. За 1 мин принтер распечатает страниц. Поэтому за t мин принтер распечатает 10t страниц.

Ответ: 2.

6. Разложим знаменатель второй дроби на множители, приведем дроби к общему знаменателю и вычтем их. Получим:

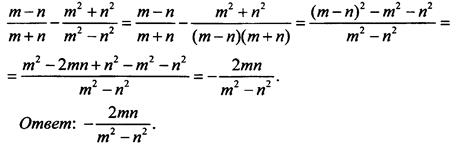
7. Используя свойства действий со степенями, найдем значение выражения:

Ответ: 1.

8. Во втором выражении вынесем множитель из-под корня и упростим выражение:

Ответ:

9. Все члены уравнения умножим на 6 и получим откуда х = 5,4.

Ответ: 4.

10. Для приведенных квадратных уравнений найдем дискриминанты и получим:

(имеет 2 корня);

(имеет 2 корня);

(имеет 2 корня);

(не имеет корней).

Видно, что только уравнение 4 не имеет корней.

Ответ: 4.

11. Учтем, что второе уравнение системы задает параболу, направленную ветвями вверх. Рассмотрим три приведенные системы и получим:

1) парабола у = х² выходит из начала координат и пересекает окружность х² + у² = 4 в двух точках. Поэтому такая система уравнений имеет два решения, т. е. 1 → в;

2) парабола у = х² + 2 выходит из точки (0; 2) и имеет с окружностью x² + y² = 4 только эту одну общую точку. Поэтому такая система уравнений имеет одно решение, т. е. 2 → б;

3) парабола у = х² + 3 выходит из точки (0; 3) и располагается выше окружности х² + у² = 4, т. е. не имеет с ней общих точек. Поэтому такая система уравнений не имеет решений, т. е. 3 → а.

Ответ: 1 → в; 2 → б; 3 → а.

12. Решим приведенное линейное неравенство 9х - 3 > 10х - 2 и получим: -3 + 2 > 10х - 9х или -1 > х, т. е. х < -1. Видно, что число 4) -0,7 не входит в этот промежуток.

Ответ: 4.

13. Так как a > b и b ≤ с, то сравнить числа а и с невозможно. Например, на верхней шкале a > с, а на нижней, наоборот, a < с.

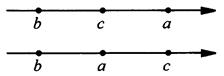
Ответ: 4.

14. Посчитаем число мест в рядах: 10, 11, 12, ... . Видно, что эти числа образуют арифметическую прогрессию с первым членом a₁ = 10 и разностью d = 1. Найдем сумму n = 15 первых членов прогрессии. Получаем: или (мест).

Ответ: 1.

15. Если функция у = f(х) возрастает на промежутке (-∞; 1], то она имеет наибольшее значение при х = 1. При этом значении функции при х = 0: f(0) = 2. Этим условиям удовлетворяет только функция, график которой изображен на рис. 1.

Ответ: 1.

16. Из графика видно, что в начале месяца бензин стоил 10 руб., в конце месяца - 12 руб. Поэтому цена бензина увеличилась на 12- 10 = 2 руб., что составляет от первоначальной цены.

Ответ: 2.

17. Так как из 1000 электрических лампочек 5 бракованных, то исправных лампочек 1000 - 5 = 995 штук. Поэтому вероятность купить исправную лампочку

Ответ: 0,995.

18. Запишем варианты измерения в порядке возрастания и получим сгруппированный ряд данных: 130, 132, 134, 158, 166. Среднюю варианту в этом ряду называют медианой (т. е. медиана равна 134). Найдем также среднее арифметическое этого набора чисел: Тогда среднее арифметическое набора чисел отличается от его медианы на 144 - 134 = 10 (см).

Ответ: 10 см.

Часть 2

19 (2). Разложим числитель и знаменатель дроби на множители и сократим ее. В числителе найдем корни квадратного трехчлена, в знаменателе используем группировку членов и вынесение общего множителя за скобки. Получаем: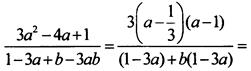     

Ответ:

20 (4). Построим сначала график функции у = х(х - 2) - пунктирная парабола. Оставим тот участок кривой, для которого х ≥ 0. Теперь построим график функции у = x(2 - х). Так как х(2 - х) = -х(х - 2), то при х < 0 надо отразить пунктирную часть параболы вниз. Поэтому графиком данной функции является сплошная кривая. Видно, что значения функции f(x) < 0 при х < 0 и 0 < х < 2.

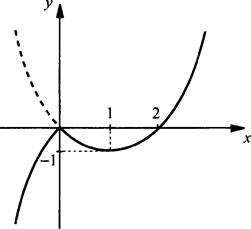
Ответ: f(x) < 0 при х < 0 и 0 < х < 2.

21 (4). Пусть на первой машине можно сделать копию пакета документов за t мин, тогда на второй - за t + 15 мин. Производительность машин соответственно (при этом весь объем работы принят за единицу). Так как при одновременной работе двух машин копию можно сделать за 10 мин, то получаем уравнение: Корни этого уравнения t = 15 и t = -10 (не подходит). Итак, работа будет сделана на первой машине за 15 мин, на второй - за 30 мин.

Ответ: на первой машине за 15 мин, на второй - за 30 мин.

22 (6). Пусть уравнение прямой у = кх + b. Так как ее график проходит через точки А(3; 15) и В(9; 5), то их координаты удовлетворяют уравнению прямой. Получаем систему линейных уравнений: Вычтем из первого уравнения второе: 10 = -6k, откуда Подставим это значение в первое уравнение: откуда b = 20. Итак, уравнение прямой Эта прямая также проходит через точку С(24; m). Получаем:

Ответ: m = -20.

23 (6). Так как число 0 находится между корнями уравнения то произведение корней уравнения (по формуле Виета) (2 - k)(2 + k) < 0. Решение этого неравенства k < -2 и k > 2. Проверим, что уравнение имеет корни. Найдем: т. е. при всех значениях к данное уравнение имеет решения.

Ответ: при k < -2 и k > 2.