Алгебра и начала анализа 10 класс поурочные планы по учебнику Мордковича А. Г.
Преобразование сумм тригонометрических функций в произведение - Преобразование тригонометрических выражений - 1-е полугодие
Цель: продолжить изучение основных тригонометрических формул.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (тест).
Вариант 1
1. Вычислите ![]()
Ответы: ![]()
2. Вычислите sin(2 arctg 3).
Ответы:
![]()
3. Упростите выражение ![]()
Ответы: ![]()
4. Решите уравнение ![]()
Ответы: ![]()
Вариант 2
1. Вычислите ![]()
Ответы ![]()
2. Вычислите cos(2 arctg 4).
Ответы: ![]()
3. Упростите выражение ![]()
Ответы: ![]()
4. Решите уравнение ![]()
Ответы: ![]()
III. Изучение нового материала
Приведем следующую группу формул - формулы, с помощью которых можно преобразовать суммы тригонометрических формул в произведения:
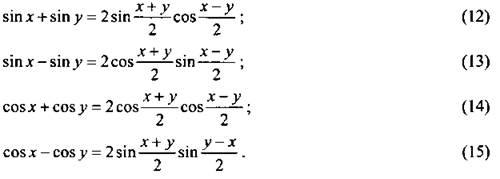
Пример 1
Выведем формулу (14).
Представим углы х и у в виде ![]() воспользуемся формулами (5) и (4) и получим:
воспользуемся формулами (5) и (4) и получим: ![]()
![]()

Пример 2
Преобразуем в произведение А ![]() Сгруппируем члены этого выражения и используем приведенные формулы:
Сгруппируем члены этого выражения и используем приведенные формулы: ![]()
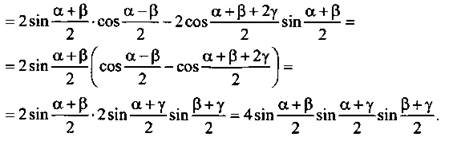
Пример 3
Упростим выражение ![]()
Воспользуемся формулами (7) и (12): ![]()
![]()
Пример 4
Решим уравнение:

а) Перенесем все члены уравнения в левую часть: sin 12х - sin 2х = 0 - и преобразуем разность синусов в произведение: ![]() или
или ![]() Получим совокупность уравнений
Получим совокупность уравнений ![]() и
и ![]()
б) В отличие от предыдущей задачи в данном случае функции разноименные. Поэтому используем формулу приведения  Преобразуем сумму косинусов в произведение:
Преобразуем сумму косинусов в произведение: 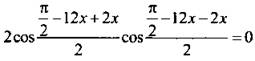 или
или ![]() Учтем четность функции косинуса:
Учтем четность функции косинуса: ![]() Приходим к совокупности уравнений
Приходим к совокупности уравнений 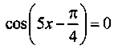 (тогда
(тогда ![]() и
и ![]() ) и
) и ![]() (тогда
(тогда ![]() ).
).
в) Сгруппируем члены уравнения ![]() Преобразуем суммы синусов в произведения:
Преобразуем суммы синусов в произведения: ![]()
![]() Вынесем общий множитель за скобки:
Вынесем общий множитель за скобки: ![]() Преобразуем сумму косинусов в произведение:
Преобразуем сумму косинусов в произведение: ![]() Получим совокупность уравнений sin 3x = 0 (тогда
Получим совокупность уравнений sin 3x = 0 (тогда ![]() ), cos 3x/2 = 0 (тогда
), cos 3x/2 = 0 (тогда ![]() и
и ![]() ) и cos x/2 = 0 (тогда
) и cos x/2 = 0 (тогда ![]() ). Заметим, что решения
). Заметим, что решения ![]() можно объединить одной формулой
можно объединить одной формулой ![]()
Пример 5
Построим график уравнения: a) sin 2y = sin 4x; б) cos у = cos х2.
Найдем более простую связь между переменными у и х. Для этого преобразуем разность тригонометрических функций в произведение,
а) Получим: sin 2y – sin 4x = 0 или 2 cos(y + 2x)sin(y - 2x) = 0. Приходим к совокупности уравнений cos(y + 2x) = 0 (тогда ![]() и
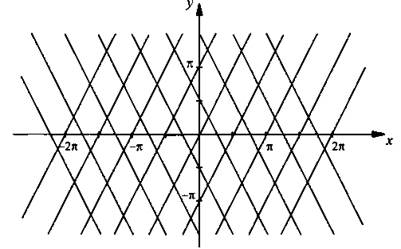
и ![]() ) и sin(y - 2х) = 0 (тогда у - 2х = πn и у = 2х + πn). Таким образом, придавая n различные значения, строим два семейства прямых:
) и sin(y - 2х) = 0 (тогда у - 2х = πn и у = 2х + πn). Таким образом, придавая n различные значения, строим два семейства прямых: ![]() (параллельные прямые).
(параллельные прямые).
б) Получим: cos у - cos х2 = 0 или ![]() Приходим к совокупности уравнений
Приходим к совокупности уравнений ![]() (тогда
(тогда ![]() и
и ![]() ) и
) и ![]() (тогда
(тогда ![]() и
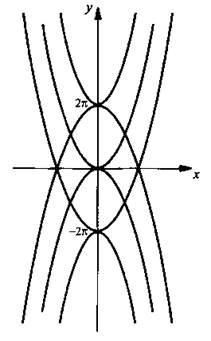
и ![]() ). Строим эти семейства парабол.
). Строим эти семейства парабол.
Рассмотрим теперь метод вспомогательного угла. Он используется для преобразования выражений вида A sin x + B cos x к одной тригонометрической функции. Данное выражение (обозначим его z) умножим и разделим на число ![]() Получим:
Получим: ![]() Легко проверить, что выполняется равенство
Легко проверить, что выполняется равенство  Поэтому можно считать, что A/C и B/C — значения тригонометрических функции некоторого (вспомогательного) угла t:
Поэтому можно считать, что A/C и B/C — значения тригонометрических функции некоторого (вспомогательного) угла t: ![]() Тогда выражение z можно записать в виде
Тогда выражение z можно записать в виде ![]() При этом угол t можно найти из равенства
При этом угол t можно найти из равенства ![]() Но так как число С записывают в виде радикала, то получают равенство tg t = B/A, из которого находят угол t = arctg B/A.
Но так как число С записывают в виде радикала, то получают равенство tg t = B/A, из которого находят угол t = arctg B/A.
Таким образом, выражение z = A sin x + B cos x можно записать в виде z = C sin(x + t), где ![]() и t = arctg B/A.
и t = arctg B/A.
Пример 6
Преобразуем выражение z = sin х + 2 cos х.
В данном случае коэффициенты А = 1, В = 2. Найдем число ![]() (тогда t = arctg 2). Получим:
(тогда t = arctg 2). Получим: ![]() где t = arctg 2.
где t = arctg 2.
Заметим, что выражение z = A sin x + B cos x можно привести и к виду ![]() где
где ![]() Для этого обозначим
Для этого обозначим ![]() и
и ![]() тогда
тогда ![]()
Пример 7
Преобразуем выражение z = sin s + 2 cos x.
Запишем данное выражение в виде ![]()
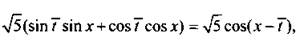 где
где ![]()
Пример 8
Найдем наименьшее и наибольшее значения выражения z = 3 sin x + 4 cos x + 7.
Представим выражение ![]() в виде одного синуса. В данном случае А = 3 и В = 4. Найдем
в виде одного синуса. В данном случае А = 3 и В = 4. Найдем ![]() умножим и разделим выражение
умножим и разделим выражение ![]() на число С. Получим:
на число С. Получим: ![]() Обозначим
Обозначим ![]() (тогда
(тогда ![]() ). Запишем выражение
). Запишем выражение ![]() в виде
в виде ![]() Тогда выражение имеет вид: z = 5 sin(x + t) + 7. Оценим это выражение. В силу ограниченности синуса получим неравенство
Тогда выражение имеет вид: z = 5 sin(x + t) + 7. Оценим это выражение. В силу ограниченности синуса получим неравенство ![]() Умножим все части этого неравенства на положительное число 5 (при этом знаки неравенства сохраняются):
Умножим все части этого неравенства на положительное число 5 (при этом знаки неравенства сохраняются): ![]() Ко всем частям неравенства прибавим число 7 и получим:
Ко всем частям неравенства прибавим число 7 и получим: ![]() или
или ![]() Итак, имеем: zнaим = 2 и zнaиб = 12.
Итак, имеем: zнaим = 2 и zнaиб = 12.
Пример 9
Решим уравнение ![]()
Первые два слагаемых приведем к функции косинуса. Для этого умножим и разделим их на число ![]() Получим:
Получим:  Обозначим
Обозначим ![]() отсюда
отсюда ![]() Тогда уравнение имеет вид:
Тогда уравнение имеет вид: ![]() или
или ![]() Преобразуем сумму функций в произведение:
Преобразуем сумму функций в произведение: 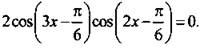 Приходим к совокупности уравнений:
Приходим к совокупности уравнений: ![]() (тогда
(тогда ![]() (тогда
(тогда ![]() и
и ![]() ). .
). .
IV. Контрольные вопросы
1. Формулы преобразования сумм тригонометрических функций в произведения (фронтальный опрос).
2. Метод вспомогательного угла.
V. Задание на уроках
§ 22, № 1 (а, б); 4 (в, г); 5 (а, б); 6 (а, г); 9 (а); 11 (б); 12 (а, б); 14 (а); 16 (в, г); 17 (а, б); 18 (б); 19 (а, б); 20 (а); 21 (б); 22 (а).
VI. Задание на дом
§ 22, № 1 (в, г); 4 (а, б); 5 (в, г); 6 (б, в); 9 (б); 11 (а); 12 (в, г); 14 (б); 16 (а, б); 17 (в, г); 18 (а); 19 (в, г); 20 (б); 21 (а); 22 (б).
VII. Творческие задания
1. Запишите в виде одной тригонометрической функции:

Ответы: ![]()

2. Решите уравнение или неравенство:
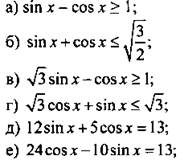
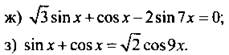
Ответы: ![]()
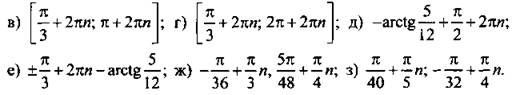
VIII. Подведение итогов уроков