Преобразование графиков (факультативное занятие) - Числовые функции - 1-е полугодие

Цель: освоить основные способы преобразования графиков.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Найдите область определения функции:

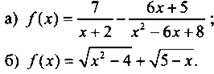
2. Начертите график какой-нибудь функции f(х), для которой

Вариант 2

1. Найдите область определения функции:

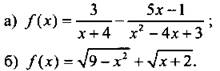
2. Начертите график какой-нибудь функции f(х), для которой

III. Изучение нового материала

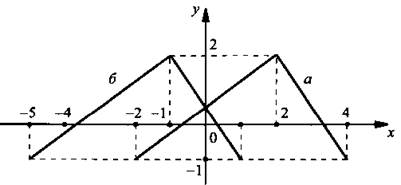
Способы преобразования графиков позволяют строить графики достаточно сложных функций, используя базовые графики линейной, квадратичной, дробно-линейной, степенной и других функций. Такие способы преобразования являются универсальными и пригодны для любых функций. Для простоты построения будем рассматривать кусочно-линейную функцию f(x) с областью определения D(x), график которой представлен на рисунке.

Будем обозначать через (х'; у') координаты точки, в которую переходит произвольная точка (х; у) плоскости при данном преобразовании. Рассмотрим эти преобразования.

1) Параллельный перенос вдоль оси ординат на вектор (0; b)

При данном преобразовании получаем: и произвольная точка графика (х; f(х)) переходит в точку (х; f(x) + b). Это означает, что график функции f(х) переходит в фигуру, состоящую из всех точек (х; f(x) + b), где х ∈ D(f). По определению такая фигура является графиком функции у = f(x) + b. В соответствии с изложенным сформулируем правило: для построения графика функции у = f(x) + b (где b – постоянное число) надо перенести график функции у = f(x) на вектор (0; b) вдоль оси ординат.

Пример 1

Для представленной функции у = f(x) построим график функции: а) y = f(x) + 2; б) у = f(x) - 1.

а) В соответствии с правилом переносим график функции у = f(x) на вектор (0; 2), т. е. на 2 единицы вверх вдоль оси ординат;

б) в соответствии с правилом переносим график функции у = f(x) на вектор (0; -1), т. е. на 1 единицу вниз вдоль оси ординат.

2) Растяжение вдоль оси ординат с коэффициентом m

Такое преобразование задается формулами и произвольная точка графика (х; f(х)) переходит в точку (х; mf(x)). Это означает, что график функции f(x) переходит в фигуру, состоящую из всех точек (х; mf(x)), где х ∈ D(f). Такая фигура является графиком функции у = mf(х). Итак, имеет место следующее правило: для построения графика функции у = mf(x) надо растянуть график функции у = f(x) в m раз вдоль оси ординат.

Пример 2

Построим график функции: а) у = 2f(х); б) у = -0,5f(х).

а) В соответствии с правилом растягиваем график функции у = f(х) в 2 раза вдоль оси ординат;

б) в соответствии с правилом растягиваем график функции у = f(х) в -0,5 раза вдоль оси ординат.

Отметим, что если 0 < lkl < 1, то растяжение с коэффициентом k фактически является сжатием. Поэтому растяжение с коэффициентом 0,5 является сжатием в 2 раза. При k < 0 для построения графика функции у = kf(x) надо сначала растянуть график функции у = f(x) в |k| раз, а затем отразить его симметрично относительно оси абсцисс.

3) Параллельный перенос вдоль оси абсцисс на вектор (-а; 0)

Это преобразование описывается формулами Каждая точка графика функции f(x) переходит в точку (х - a, f(x)). Поэтому с помощью переменных х' и у' можно записать, что график f переходит в фигуру Ф, состоящую из точек (x'; f(x' + а)), где х' принимает все значения х + а. Именно при этих значениях х' число х' - а принадлежит D(f) и f(x' + а) определено. Поэтому фигура Ф есть график функции (x'; f(x' + а)). Итак, запомните правило: график функции у = f(x + а) получается из графика функции f(x) переносом вдоль оси абсцисс на вектор (-а; 0). При а < 0 вектор (-а; 0) направлен в положительном направлении оси абсцисс, при а > 0 - в отрицательном.

Пример 3

Построим график функции: а) у = f(x - 2); б) у = f(x + 1).

а) Переносим график функции вдоль оси абсцисс на вектор (2; 0), т. е. смещаем его на 2 единицы вправо;

б) переносим график функции вдоль оси абсцисс на вектор (-1; 0), т. е. смещаем его на 1 единицу влево.

4) Растяжение вдоль оси абсцисс с коэффициентом k

Такое преобразование задается формулами 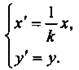Произвольная точка графика функции f(x) при этом переходит в точку (; f(x)). Для переменной х’, у' можно утверждать, что график функции у = f(x) переходит в фигуру, состоящую из точек (x'; f(kx)), где х' принимает все значения , а х ∈ D(f). Эта фигура есть график функции у = f(kx). Таким образом, существует правило: для построения графика функции у = f(kx) надо сжать график функции f(x) с коэффициентом к вдоль оси абсцисс.

Пример 4

Построим график функции: а) у = f(0,5x); б) у = f(2х).

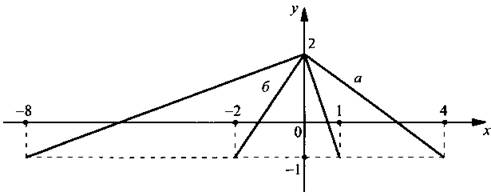
а) Запишем функцию в виде у = f(x/2). В соответствии с правилом для построения графика этой функции надо график функции у = f(x) растянуть в 2 раза вдоль оси абсцисс;

б) запишем функцию в виде у = f(2x). График этой функции получается из графика функции у = f(x) растяжением в 0,5 раза. Так как k = 2 и |k| > 1, то фактически это означает сжатие графика у = f(x) в k = 2 раза вдоль оси абсцисс.

Рассмотрим частные случаи преобразований 2 и 4, наиболее распространенные на практике.

5) Отражение относительно оси абсцисс

Это преобразование является частным случаем преобразования 2 для m = -1 и описывается формулами 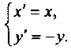Тогда имеет место правило: для построения графика функции у = -f(x) надо график функции y = f(x) отразить относительно оси абсцисс.

Пример 5

Построим график функции у = -f(x).

В соответствии с правилом отражаем симметрично относительно оси абсцисс график функции у = f(x) и получаем график функции y = -f(x).

6) Отражение относительно оси ординат

Такое преобразование является частным случаем преобразования 4 для k = -1 задаётся формулами Существует правило: для построения графика функции у = f(-x) надо график функции у = f(x) симметрично отразить относительно оси ординат.

Пример 6

Построим график функции у = f(-x).

Отразим график функции у = f(x) симметрично относительно оси ординат и получим график функции у =f(-x).

Обязательно надо запомнить шесть изложенных правил преобразования графиков. Еще раз напомним, что эти правила являются универсальными и применимы для любых функций. Остановимся теперь на использовании этих правил для построения графиков конкретных функций.

Пример 7

Построим график дробно-линейной функции .

В функции y(x) выделим целую часть Из этой записи видно, что для построения графика функции надо график функции у = 1/x сместить на 1 единицу влево вдоль оси абсцисс и на 2 единицы вверх вдоль оси ординат.

Пример 8

Построим график функции у = 3 - |х - 2|.

Запишем функцию в виде у = -|х - 2| + 3. Из такой записи следует, что для построения графика функции у = 3 - |х - 2| надо график функции у = |x| отразить относительно оси абсцисс, затем этот новый график сместить на 2 единицы вправо вдоль оси абсцисс и на 3 единицы вверх вдоль оси ординат.

IV. Контрольный вопрос

Объясните, как с помощью графика функции у = х2 построить график функции: а) у = х2 - 3; б) у = (х + 1)2; в) у = -х2; г) у = (-х)2; д) у = 2х2; е) у = (х/2)2.

V. Задание на уроках

§ 1, № 9 (а, г); 11 (а, б); 14 (а, в).

VI. Задание на дом

§ 1, № 9 (б, в); 11 (в, г); 14 (б, г).

VII. Творческое задание

Используя приведенный график функции у = f(x), постройте график функции:

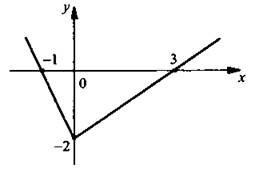
VIII. Подведение итогов уроков