Алгебра и начала анализа 10 класс поурочные планы по учебнику Мордковича А. Г.
Итоги контрольной работы - урок 4 - Преобразование тригонометрических выражений - 2-е полугодие
Цели: сообщить результаты работы; рассмотреть типичные ошибки; разобрать трудные задачи.
Ход урока
I. Сообщение темы и целей урока
II. Итоги контрольной работы
III. Ответы и решени.
Вариант 1
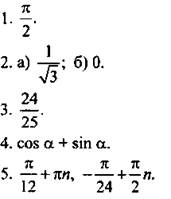
Вариант 2
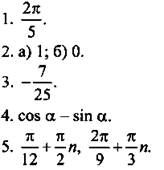
Вариант 3
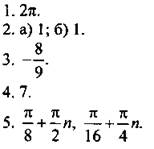
Вариант 4
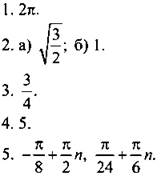
Вариант 5
1. Преобразуем произведение функций в сумму и используем формулу для sin 2x. Тогда получим: ![]() Выпишем периоды функций, входящих в у(х):
Выпишем периоды функций, входящих в у(х): ![]()
![]() Найдем НОК (10, 18, 45) = 90. Тогда период данной функции
Найдем НОК (10, 18, 45) = 90. Тогда период данной функции ![]()
Ответ: 2π.
2. Упростим первое число: ![]()
 В первой четверти функция у = tg х возрастает и принимает положительные значения. Тогда tg27° > tg5° > 0 и отношение
В первой четверти функция у = tg х возрастает и принимает положительные значения. Тогда tg27° > tg5° > 0 и отношение  Соответственно, второе число
Соответственно, второе число ![]() Поэтому первое число больше.
Поэтому первое число больше.
Ответ: первое число больше.
3. Используем формулу понижения степени и запишем функцию в виде ![]() Обозначим z = cos 6x (где z ∈ [-1; 1]) и получим квадратичную функцию у = -2z2 + 2z + 3. Наибольшее значение функции достигается при z = 1/2, и
Обозначим z = cos 6x (где z ∈ [-1; 1]) и получим квадратичную функцию у = -2z2 + 2z + 3. Наибольшее значение функции достигается при z = 1/2, и ![]() Наименьшее значение функции достигается при z = -1, и унаим = -2 · 1 - 2 + 3 = -1.
Наименьшее значение функции достигается при z = -1, и унаим = -2 · 1 - 2 + 3 = -1.
Ответ: унаим = -1, унаи6 = 3,5.
4. Преобразуем данное равенство ![]() и получим:
и получим: ![]() или 7 cos x = 6 sin x, откуда tg x = 7/6. Найдем
или 7 cos x = 6 sin x, откуда tg x = 7/6. Найдем 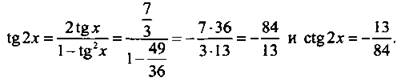
Ответ: -13/84.
5. Используя соответствующие формулы, выполним преобразования: ![]()
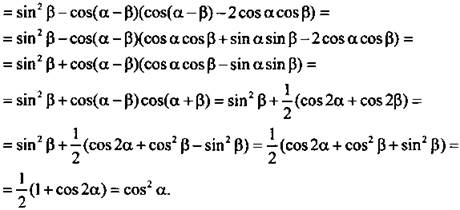
Ответ: cos2 а.
6. Запишем уравнение в виде ![]() или
или ![]() Преобразуем разность функций в произведение
Преобразуем разность функций в произведение ![]() Получим совокупность уравнений
Получим совокупность уравнений ![]() (тогда
(тогда ![]() и
и ![]() ) и
) и ![]() (тогда
(тогда ![]() и
и ![]() ).
).
Ответ: ![]()
Вариант 6
1. Преобразуем произведение функций в сумму и используем формулу для cos 2x. Тогда получим: ![]() Выпишем периоды функций, входящих в у(х):
Выпишем периоды функций, входящих в у(х): ![]()
![]() Найдем НОК (10, 26, 65) = 130. Тогда период данной функции
Найдем НОК (10, 26, 65) = 130. Тогда период данной функции ![]()
Ответ: 2π.
2. Упростим первое число: ![]()
![]() В первой четверти функция у = tg ч возрастает и принимает положительные значения. Тогда tg11° > tg1° > 0 и отношение
В первой четверти функция у = tg ч возрастает и принимает положительные значения. Тогда tg11° > tg1° > 0 и отношение  Соответственно, второе число
Соответственно, второе число 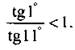 Поэтому первое число больше.
Поэтому первое число больше.
Ответ: первое число больше.
3. Используем формулу понижения степени и запишем функцию в виде ![]() Обозначим z = cos 4x (где z ∈ [-1; 1]) и получим квадратичную функцию y = 3z2 + 3z + 8. Наименьшее значение функции достигается при z = -1/2, и
Обозначим z = cos 4x (где z ∈ [-1; 1]) и получим квадратичную функцию y = 3z2 + 3z + 8. Наименьшее значение функции достигается при z = -1/2, и ![]() Наибольшее значение функции достигается при z = 1, и унаиб = 3 + 3 + 8 = 14.
Наибольшее значение функции достигается при z = 1, и унаиб = 3 + 3 + 8 = 14.
Ответ: ![]()
4. Преобразуем данное равенство ![]() и получим:
и получим: ![]() или -9 cos x = 5 sin x, откуда tg x = -9/5. Найдем
или -9 cos x = 5 sin x, откуда tg x = -9/5. Найдем 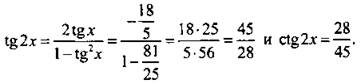
Ответ: 28/45.
5. Используя соответствующие формулы, выполним преобразования: ![]() = cos2 Р + cos(a - P)(cos(a - Р) - 2 cos a cos Р) =
= cos2 Р + cos(a - P)(cos(a - Р) - 2 cos a cos Р) =

Ответ: sin2 a.
6. Запишем уравнение в виде ![]() или
или ![]() Преобразуем разность функций в произведение
Преобразуем разность функций в произведение ![]() Получим совокупность уравнений
Получим совокупность уравнений ![]() (
(![]() ) и
) и ![]() (тогда
(тогда ![]() ).
).
Ответ: ![]()