Алгебра и начала анализа для учащихся 11 класса поурочные планы
повторить определение производной; вспомнить производные функций у = sinx, у = cosx, у = tgx, у = ctgx; закрепить правила вычисления производных - ПОВТОРЕНИЕ: ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ, ПРОИЗВОДНЫЕ ФУНКЦИЙ у = sinx, у = соsx, у = tgx, у = ctgx, у = xn, ГДЕ n∈Z, n ≠ -1. ПРАВИЛА ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ, ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ (3 Ч) - 1-е полугодие
Цели: повторить определение производной; вспомнить производные функций у = sinx, у = cosx, у = tgx, у = ctgx; закрепить правила вычисления производных.
Ход урока
I. Повторение пройденного материала
1. Сформулируйте определение производной функции в точке.
2. Сформулируйте правила вычисления производных.
3. Запишите производные функций у = sinx, у = cosx, y = tgx, у = ctgx.
4. Чему равна производная функции f(x) = хn, где n∈Z, n ≠ -1?
II. Вычисление производных функций
1. Найти производную функции f(x):
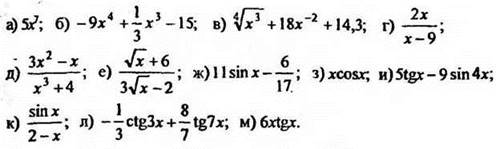
2. Вычислить значение производной функции:
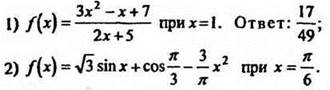
Решение
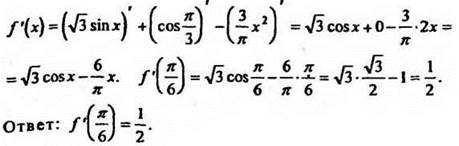
3. Найти значения производных функций при заданных значениях аргумента (часть этих заданий учащиеся решают самостоятельно):
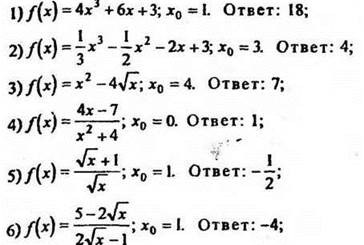
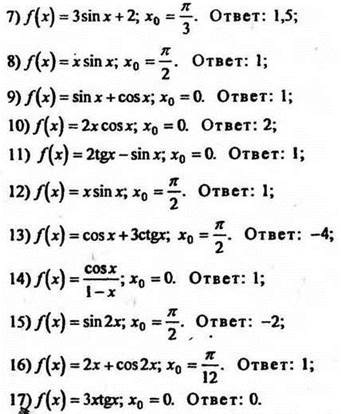
4. Повторить применения непрерывности. Решите неравенство методом интервалов:
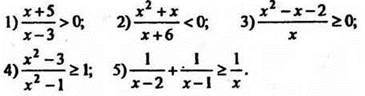
5. Найти наименьшее целое число, входящее в область определения каждой из функций:
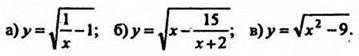
III. Итоги урока
IV. Домашнее задание: из § 4 повторить п. 12 -25; решить на стр. 292-293 № 219, № 223(a), № 224.