Алгебра и начала анализа для учащихся 11 класса поурочные планы
Площадь криволинейной трапеции - ОБОБЩАЮЩЕЕ ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ И НАЧАЛ АНАЛИЗА - 2-е полугодие
УРОК № 8
Тема. Площадь криволинейной трапеции
Цели: упражнять учащихся в нахождении площади криволинейной трапеции.
Ход урока
I. Анализ домашней контрольной работы
1. Указать ошибки, сделанные учащимися в работе.
2. Выполнить 4-е задание из работы (проверить его решение): найти область определения функции 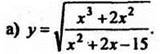
Решение
Функция у = ![]() определена, если значение подкоренного выражения неотрицательно:
определена, если значение подкоренного выражения неотрицательно:
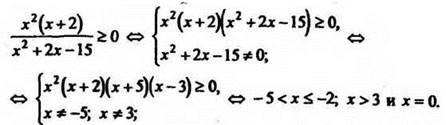

Ответ: (-5;-2]U(3;∞) и х=0;

Указание
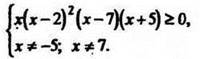
![]()
Рис. 63
Ответ: (-5;0]U(7;∞) и х = 2.
II. Нахождение площади криволинейной трапеци.
1. Вычислите площадь фигуры, ограниченной линиями
![]()

Рис. 64
Решение
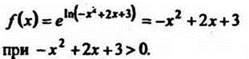
Находим координаты вершины параболы ![]()
![]()
Находим площадь фигуры:

2. На параболе ![]() найдите точки, ближайшие к началу координат.
найдите точки, ближайшие к началу координат.
Решение
Пусть N(x;y) - точка, лежащая на параболе ![]() . Найдём расстояние от этой точки до начала координат,
. Найдём расстояние от этой точки до начала координат, 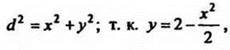 то
то 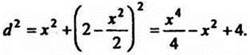 Рассмотрим функцию
Рассмотрим функцию ![]()
![]() Функция f(x) непрерывна на R, т. к. это целая рациональная функция и дифференцируемая на R. Найдём критические точки f(x):
Функция f(x) непрерывна на R, т. к. это целая рациональная функция и дифференцируемая на R. Найдём критические точки f(x):
 х = 0 или
х = 0 или ![]() Эти точки принадлежат области определения функции.
Эти точки принадлежат области определения функции.

Рис. 65
![]()
При переходе через точки ![]() производная меняет знак с минуса на плюс. Значит,
производная меняет знак с минуса на плюс. Значит, ![]() есть точки минимума. Минимум функции в этих точках есть её наименьшее значение, т. к. на R только две точки минимума.
есть точки минимума. Минимум функции в этих точках есть её наименьшее значение, т. к. на R только две точки минимума.
Если ![]() точка (-
точка (-![]() ;1); если х =
;1); если х = ![]() , то
, то ![]() точка (
точка (![]() ;1). Ответ: точки параболы, ближайшие к началу координат (-
;1). Ответ: точки параболы, ближайшие к началу координат (-![]() ;1) и (
;1) и (![]() ;1).
;1).
3*. Найти площадь фигуры, ограниченной параболой у = х2 +10 и касательными к этой параболе, проведёнными из точки (0;1).
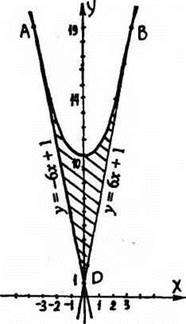
Рис. 66
Решение
Неизвестна абсцисса точки касания х = а. Чтобы её найти, составим уравнение касательной: ![]()
Имеем ![]() значит,
значит, ![]() уравнение касательной имеет вид.
уравнение касательной имеет вид.
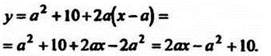
Уравнение касательной
![]()
По условию касательная должна проходить через точку (0;1), то есть координаты точки (0;1) должны удовлетворять уравнению (1):
![]()
Подставим найденные значения в уравнение (1).
если ![]()
если ![]()
Получили два уравнения касательных ![]() Параболы y = х2 + 10 они касаются в точках А(-3;19) и В(3;19).
Параболы y = х2 + 10 они касаются в точках А(-3;19) и В(3;19).
Найдём площадь фигуры DACB:
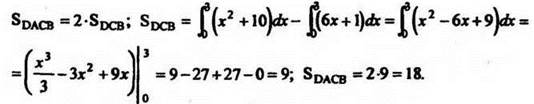
Ответ: 18.
4. Найти площадь фигуры, ограниченной линиями ![]()
Решение
Построим графики функций ![]()
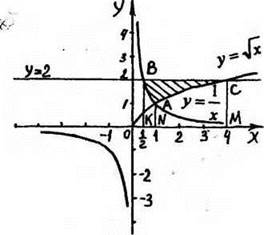
Рис. 67
Найдём пределы интегрирования:
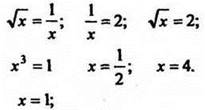
Пределы интегрирования:

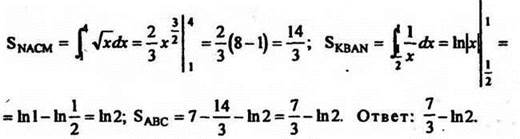
III. Итоги урока
IV. Домашнее задание: повторить из § 9 п. 32, 33; решить на стр. 298 № 275, № 276.