Возведение в степень произведения и степени - ІІ четверть - Степень с натуральным показателем

ЦЕЛЬ УРОКА: Добиться усвоения учащимися правил возведения в степень произведения и степени и умения применять эти правила.

ПЛАН УРОКА:

№	Этап урока	Содержание	Время (мин)
1	Организационный момент	Нацелить учащихся на урок	1
2	Проверка домашнего задания	Коррекция ошибок	5
3	Устная работа	Актуализировать опорные знания	7
4	Восприятие и первичное осознание материала	Вывести правила возведения в степень произведения и степени	10
5	Тренировочные упражнения	Формировать умения применять правила возведения в степень произведения и степени	18
6	Подведение итогов урока	Обобщить теоретические сведения, полученные на уроке	2
7	Сообщение домашнего задания	Разъяснить содержание домашнего задания	2

ХОД УРОКА

I. Организационный момент.

II. Проверка домашнего заданна (фронтально).

III. Устная работа.

1) Сформулировать правило умножения степеней с одинаковыми основаниями.

2) Сформулировать правило деления степеней с одинаковыми основаниями.

3) № 533 — устно.

4) Выполнить действия:

5) Какую длину имеет ребро куба, если объем куба:

а) 27 дм3; б) 64 см3; в) 125 мм3; г) 0,125 м3?

IV. Восприятие и первичное осознание материала с применением свойств действий над числами и определения степени

(учитель ведет запись на доске, ученики в тетрадях, все действия комментируются)

Значит, (ab)4 = а4b4.

2. (аb)n = аn · bn — гипотеза.

Доказательство:

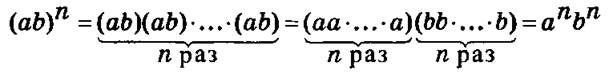
Следовательно, (ab)n — аnbn.

Ученики с помощью учителя формулируют правило и сверяют его с правилом на с. 97.

3. Пример 1 (по учебнику) с. 97.

4. № 428 (а, в, д, ж) — на доске и в тетрадях;

№ 428 (б, г, е, з) — самостоятельно с последующей проверкой.

5. № 413 — на доске и в тетрадях.

а) (с4)2 = с4 · с4 = с8. Следовательно, (с4)2 = с8.

б) (с2)4 = с2 · с2 · с2 · с2 = с8. Следовательно, (с2)4 = с8.

6. (аm)n = аmn — гипотеза.

Доказательство:

По определению степени:

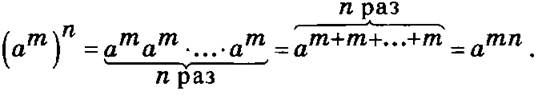
Следовательно, (аm)n = аmn.

Учащиеся с помощью учителя формулируют правило и сверяют его с правилом на с. 98.

7. Пример 2 (по учебнику), с. 98.

8. № 438 — устно.

V. Тренировочные упражнения.

№ 430 — на доске и в тетрадях. Обращаем внимание на рациональные вычисления.

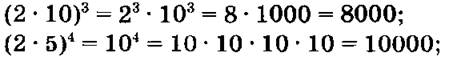
№ 437 — начать на доске и закончить самостоятельно в тетрадях с последующей проверкой.

В данном номере отрабатываем прочитывание свойства степеней справа налево: аnbn = (ab)n;

№ 439 — в тетрадях, комментируя правилами действий со степенями;

№№ 441, 442 — самостоятельно с последующей проверкой;

№ 432 — устно.

VI. Итог урока.

Повторить правила возведения произведения и степени в степень

VII. Домашнее задание.

п. 20, №№ 429, 433, 440