Поурочное планирование по алгебре 7 класс
Разложение многочлена на множители способом группировки - ІІІ четверть - Многочлены
ЦЕЛЬ УРОКА: Познакомить учащихся с разложением многочлена на множители способом группировки и начать формирование соответствующего умения.
ПЛАН УРОКА:
№ |
Этап урока |
Содержание |
Время (мин) |
1 |
Организационный момент |
Нацелить учащихся на урок |
1 |
2 |
Проверка домашнего задания |
Коррекция ошибок |
5 |
3 |
Устная работа |
Актуализация опорных знаний |
4 |
4 |
Изложение нового материала |
Познакомить учащихся с разложением многочлена на множители способом группировки |
10 |
5 |
Тренировочные упражнения |
Формировать умение раскладывать многочлен на множители способом группировки |
15 |
6 |
Упражнения на повторение |
Повторить решение задач с помощью составления уравнения |
6 |
7 |
Подведение итогов урока |
Обобщить теоретические сведения, полученные на уроке |
2 |
8 |
Сообщение домашнего задания |
Разъяснить содержание домашнего задания |
2 |
ХОД УРОКА
I. Организационный момент
II. Проверка домашнего задания (фронтально)
III. Устная работа
1) Разложить на множители:
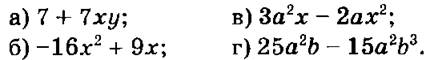
2) Разложить на множители:
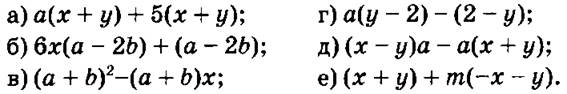
IV. Изложение нового материала
1. Способ группировки применяют к разложению на множители тех многочленов, у которых нет общего для всех членов множителя.
2. ![]()
Этот пример не вызывает затруднений, так как является упражнением на повторение.
3. Разложить на множители многочлен:
![]()
а) Все ли члены многочлена (2) имеют общий множитель? (нет);
б) Сравнить многочлены (1) и (2). (Это один и тот же многочлен, записанный по-разному);
в) Следовательно, какой ответ мы должны получить, разложив многочлен на множители? ((x + y)(m + n)).
4. Далее учитель объясняет, что надо члены, имеющие общие множители, собрать в группы и заключить в скобки. Поэтому и способ называется способом группировки. Далее решаем с подробным объяснением каждого шага:
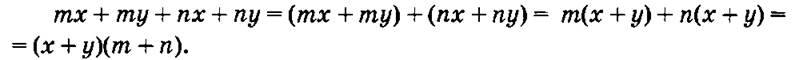
5. Читаем по учебнику п. 30 с. 141 (до примера 3).
6. Выделяем последовательность всех операций (алгоритм), которые надо выполнить:
1) Подбираем члены так, чтобы они имели общий множитель;
2) Подобранные члены объединяем в группы;
3) Группы заключаем в скобки;
4) Выносим за скобки общий множитель и получаем разложение многочлена на множители.
7. Обращаем внимание на возможную проверку полученного результата.
8. Если при группировке окажется, что группы взяты неудачно, то члены перегруппировывают.
V. Тренировочные упражнения
№№ 708, 709 — на доске и в тетрадях с подробным объяснением;
№ 711 — самостоятельно с последующей проверкой;
№ 791 (а, б, в, г) — на доске и в тетрадях.
VI. Упражнения на повторение
№ 719.
VII. Итог урока
Повторить алгоритм разложения многочлена на множители способом группировки
VIII. Домашнее задание.
п. 30 (до примера 3), №№ 710, 712, 720 (а).