Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Деление рациональных дробей - ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ - РАЦИОНАЛЬНЫЕ ДРОБИ
Цель: рассмотреть более сложные задачи, связанные с делением рациональных дробей.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Выполните деление ![]()
2. Разделите дроби ![]()
3. Упростите выражение ![]()
Вариант 2
1. Выполните деление ![]()
2. Разделите дроби ![]()
3. Упростите выражение ![]()
III. Изучение нового материала (основные понятия)
С делением рациональных дробей связано значительное число самых разнообразных задач.
Пример 1
Найдите допустимые значения переменной дробного выражения 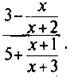 Представьте это выражение в виде дроби.
Представьте это выражение в виде дроби.
Числитель этого выражения ![]() имеет смысл при всех значениях х, кроме х = -2 (т. к. делить на нуль нельзя). Упростим это выражение:
имеет смысл при всех значениях х, кроме х = -2 (т. к. делить на нуль нельзя). Упростим это выражение: ![]() Знаменатель этого выражения
Знаменатель этого выражения ![]() имеет смысл при всех значениях х, кроме х = -3. Преобразуем это выражение:
имеет смысл при всех значениях х, кроме х = -3. Преобразуем это выражение: ![]()
![]() Эта дробь обращается в нуль, если ее числитель 2(3х + 8) = 0. Из этого уравнения найдем х = -8/3.
Эта дробь обращается в нуль, если ее числитель 2(3х + 8) = 0. Из этого уравнения найдем х = -8/3.
Теперь разделим числитель ![]() данного выражения на знаменатель
данного выражения на знаменатель ![]() используя правило деления дробей. Имеем:
используя правило деления дробей. Имеем: ![]()
![]() Итак, данное выражение имеет смысл при всех значениях х таких, что х ≠ -2, х ≠ -3 и х ≠ -8/3. После преобразований данное выражение записано в виде рациональной дроби
Итак, данное выражение имеет смысл при всех значениях х таких, что х ≠ -2, х ≠ -3 и х ≠ -8/3. После преобразований данное выражение записано в виде рациональной дроби ![]()
Пример 2
Известно, что ![]() Найдите величину
Найдите величину ![]()
По определению частного из равенства ![]() получаем: 4b + a = 3(b + a) или 4b + a = 3b + 3a, откуда b = 2а. Теперь найдем величину
получаем: 4b + a = 3(b + a) или 4b + a = 3b + 3a, откуда b = 2а. Теперь найдем величину ![]() подставив величину b = 2a. Имеем:
подставив величину b = 2a. Имеем: ![]()
![]()
Пример 3
Известно, что ![]() Докажите, что
Докажите, что ![]()
Обозначим отношения a/b и c/d буквой х. Из равенства a/b = х получим a = bх, из равенства c/d = х имеем c = dx. Найдем отношение ![]()
![]() и отношение
и отношение ![]() Сравнивая полученные отношения (равные одной и той же дроби
Сравнивая полученные отношения (равные одной и той же дроби ![]() ), видим, что
), видим, что ![]()
Пример 4
При каких натуральных значениях n выражение ![]() является целым числом?
является целым числом?
В дроби ![]() выделим целое выражение. Для этого в числителе дроби надо выделить слагаемое пропорциональное знаменателю
выделим целое выражение. Для этого в числителе дроби надо выделить слагаемое пропорциональное знаменателю ![]() Тогда, учитывая правило вычитания дробей, можем записать:
Тогда, учитывая правило вычитания дробей, можем записать: ![]() Число 2 является целым. Поэтому, чтобы данная дробь была целым числом, надо, чтобы дробь
Число 2 является целым. Поэтому, чтобы данная дробь была целым числом, надо, чтобы дробь ![]() являлась целым числом. Это возможно только в том случае, если натуральное число n + 2 будет делителем числа 9. Число 9 имеет три натуральных делителя: 1, 3 и 9.
являлась целым числом. Это возможно только в том случае, если натуральное число n + 2 будет делителем числа 9. Число 9 имеет три натуральных делителя: 1, 3 и 9.
Рассмотрим эти случаи. При n + 2 = 1 получаем n = -1 (число отрицательное), что противоречит условию задачи. Для n + 2 = 3 находим n = 1. При n + 2 = 9 имеем n = 1. Итак, только при натуральных значениях n = 1 и n = 7 дробь ![]() является целым числом. Убедимся в этом. Для n = 1 данная дробь равна
является целым числом. Убедимся в этом. Для n = 1 данная дробь равна ![]() (целое число), при n = 7 дробь равна
(целое число), при n = 7 дробь равна ![]() (также целое число).
(также целое число).
Пример 5
Найти целую и дробную часть в выражении ![]()
Аналогично предыдущей задаче в числителе дроби надо выделить слагаемые пропорциональные знаменателю, сгруппировав его члены. Получаем: ![]()
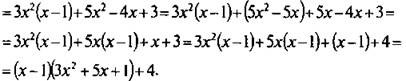
Тогда, учитывая правило сложения дробей, данное выражение можно записать в виде: ![]()
![]() Таким образом, данное выражение
Таким образом, данное выражение ![]() состоит из целой части 3х2 + 5х +1 и дробной части
состоит из целой части 3х2 + 5х +1 и дробной части ![]()
Заметим, что в примерах 4 и 5 фактически было проведено деление одного многочлена на другой. Вопрос о делимости многочленов будет рассмотрен на следующем уроке.
IV. Задание на уроке и дома
1. Найти допустимые значения переменной и упростить дробь:
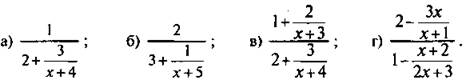
Ответы: а) ![]() при х ≠ -4 и х ≠ -5,5;
при х ≠ -4 и х ≠ -5,5;
б) ![]() при х ≠ -5 и х ≠ -16/3;
при х ≠ -5 и х ≠ -16/3;
в) ![]() при х ≠ -4, x ≠ -3 и х ≠ -5,5;
при х ≠ -4, x ≠ -3 и х ≠ -5,5;
г) 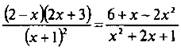 при х ≠ -1,5 и х ≠ -1;
при х ≠ -1,5 и х ≠ -1;
2. Известно, что ![]() Найдите:
Найдите:
![]()
Ответы: а) -1/3; б) 13/9; в) 13/5; г) (по условию задачи найти а = 2b).
3. Известно, что а2 + 9b2 = 6аb. Найдите.
![]()
Ответы: а) 11/4; б) 2; в) 5; г) 19/13 (по условию задачи найти a = -3b).
4. Известно, что ![]() Докажите, что:
Докажите, что:
![]()
![]() (указание: обозначьте отношение
(указание: обозначьте отношение ![]() тогда а = bt и c = td).
тогда а = bt и c = td).
5. При каких натуральных значениях n выражение является целым числом:
![]()
Ответы: а) n = 1; б) n = 2; в) n = 2 и n = 4; г)n = 3 и n = 7 (указание: в данном дробном выражении выделите целую и дробную части).
6. При каких целых значениях п выражение также является целым числом:
![]()
Ответы: а) -4; -2; 0; 2; б) -3; 1; 3; 7; в) 1; 2; 4; 5; г) -11; -5; -3; 3.
7. В дробном выражении найдите целую и дробную части:
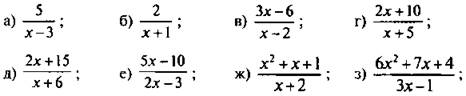
![]()
Ответы: а) целая часть 0, дробная часть ![]()
б) целая часть 0, дробная часть ![]()
в) целая часть 3, дробная часть 0;
г) целая часть 2, дробная часть 0;
д) целая часть 2, дробная часть ![]()
е) целая часть 2,5, дробная часть ![]()
ж) целая часть х - 1, дробная часть ![]()
з) целая часть 2х + 3, дробная часть ![]()
и) целая часть 3х2 - 5х + 2 , дробная часть ![]()
к) целая часть 2х2 + 3х +1, дробная часть ![]() (указание: в числителе дроби выделить слагаемые пропорциональные знаменателю).
(указание: в числителе дроби выделить слагаемые пропорциональные знаменателю).
V. Подведение итогов урока