Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Дробно-линейная функция и ее график - ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ - РАЦИОНАЛЬНЫЕ ДРОБИ
Цель: рассмотреть свойства дробно-линейной функции и построение ее графика.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Какая функция называется обратной пропорциональностью?
2. Постройте график функции у = 3/x. Найдите:
а) значение функции при x = 2,5;
б) значение аргумента, при котором у = 5.
3. График функции у = k/x проходит через точку А (2,5; -1,6). Найдите величину k.
Вариант 2
1. Какая кривая называется гиперболой?
2. Постройте график функции у = -2/x. Найдите:
а) значение функции при х = 0,8;
б) значение аргумента, при котором у = 0,4.
3. График функции проходит через точку А (-1,6; 5). Найдите величину k.
III. Изучение нового материала (основные понятия)
Рассмотрим функцию более общую, чем обратная пропорциональность. Функция ![]() (где x — независимая переменная; a, b, с, d — некоторые числа, причем с ≠ 0 и bc - ad ≠ 0) называется дробно-линейной функцией. Обратите внимание, что данная функция представляет собой дробь, числитель и знаменатель которой являются линейными функциями.
(где x — независимая переменная; a, b, с, d — некоторые числа, причем с ≠ 0 и bc - ad ≠ 0) называется дробно-линейной функцией. Обратите внимание, что данная функция представляет собой дробь, числитель и знаменатель которой являются линейными функциями.
Заметим, что требование в определении о том, что с ≠ 0 и bc - ad ≠ 0, существенно. Если это требование не выполняется, то дробно-линейная функция является на самом деле линейной (свойства и график такой функции были изучены в 7 классе).
а) Пусть с = 0 (при этом d ≠ 0). Подставив это значение в функцию ![]() , получим
, получим ![]() (где числа
(где числа ![]() ). Очевидно, что функция у = ах + Ь линейная.
). Очевидно, что функция у = ах + Ь линейная.
б) Пусть bc - ad = 0 и с ≠ 0. Выразим из этого равенства ![]() и подставим в формулу
и подставим в формулу ![]() Получаем
Получаем 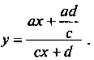 Умножим числитель и знаменатель дроби на число с. Имеем:
Умножим числитель и знаменатель дроби на число с. Имеем: 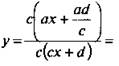
![]() — некоторое число.
— некоторое число.
В этом случае также получили частный случай линейной функции.
Пример 1
Определить вид функции ![]() и построить ее график.
и построить ее график.
Запишем данную функцию в виде ![]() Сравнивая эту функцию с дробно-линейной функцией
Сравнивая эту функцию с дробно-линейной функцией ![]() , видим что a = 2, b = -4, с = -3, d = 6. Легко проверить, что bc – ad = (-4)(-3) – 2 · 6 = 12 - 12 = 0. Поэтому данная функция не является дробно-линейной. Разложим числитель и знаменатель дроби на множители и сократим ее. Имеем:
, видим что a = 2, b = -4, с = -3, d = 6. Легко проверить, что bc – ad = (-4)(-3) – 2 · 6 = 12 - 12 = 0. Поэтому данная функция не является дробно-линейной. Разложим числитель и знаменатель дроби на множители и сократим ее. Имеем: ![]()
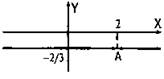
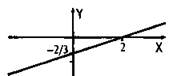
![]() (при этом x – 2 ≠ 0, т. е. х ≠ 2). Поэтому данная функция является линейной. Построим график функции у = -2/3 (горизонтальная прямая) и исключим из него точку А с абсциссой х = 2 (показана стрелками).
(при этом x – 2 ≠ 0, т. е. х ≠ 2). Поэтому данная функция является линейной. Построим график функции у = -2/3 (горизонтальная прямая) и исключим из него точку А с абсциссой х = 2 (показана стрелками).
Пример 2
Определить вид функции ![]() и построить ее график.
и построить ее график.
Сравнивая эту функцию с дробно-линейной функцией ![]() , видим, что а = 2, b = -4, с = 0, d = 6. Поэтому данная функция не является дробно-линейной. Используя свойство сложения дробей, запишем функцию в виде
, видим, что а = 2, b = -4, с = 0, d = 6. Поэтому данная функция не является дробно-линейной. Используя свойство сложения дробей, запишем функцию в виде ![]() Поэтому данная функция является линейной. Построим график этой функции
Поэтому данная функция является линейной. Построим график этой функции ![]()
Можно показать, что графиком дробно-линейной функции ![]() (при с ≠ 0 и bc - ad ≠ 0) будет гипербола, сдвинутая вдоль оси абсцисс и оси ординат. Такой сдвиг является одним из способов построения графика этой функции (такой способ будет изучаться в 9 классе). Здесь мы рассмотрим другой способ построения. Для этого перечислим и обсудим свойства дробно-линейной функции.
(при с ≠ 0 и bc - ad ≠ 0) будет гипербола, сдвинутая вдоль оси абсцисс и оси ординат. Такой сдвиг является одним из способов построения графика этой функции (такой способ будет изучаться в 9 классе). Здесь мы рассмотрим другой способ построения. Для этого перечислим и обсудим свойства дробно-линейной функции.
1. Область определения функции — множество всех значений х, кроме х = -d/c (т. к. при таком значении знаменатель сх + d = 0).
2. Точка пересечения графика функции с осью ординат у = b/d при d ≠ 0, такой точки не существует при d = 0. Для ее определения подставим значение х = 0 в формулу, задающую функцию.
3. Точка пересечения графика функции с осью абсцисс х = -b/a при а ≠ 0 и такой точки не существует при а = 0. Для ее определения положим у = 0 в формуле ![]() и решим уравнение
и решим уравнение ![]() или 0 = ах + b.
или 0 = ах + b.
4. Вертикальная асимптота графика функции имеет уравнение х = -d/c, т. к. для такого значения х функция не определена и при приближении к этому значению |у| возрастает.
5. Горизонтальная асимптота графика функции имеет уравнение у = a/c, т. к. при больших значениях |х| числитель ах + b = ах и знаменатель сх + d = сх и функция ![]()
6. Графиком функции является гипербола, ветви которой симметричны относительно точки пересечения асимптот. Ветви гиперболы не пересекают асимптоты графика.
Видно, что свойства дробно-линейной функции обобщают свойства обратной пропорциональности у = k/x. Это понятно, т. к. функция у = k/x является частным случаем функции ![]() при a = 0, d = 0 и b/c = k. Используя перечисленные свойства, легко построить эскиз графика дробно-линейной функции.
при a = 0, d = 0 и b/c = k. Используя перечисленные свойства, легко построить эскиз графика дробно-линейной функции.
Пример 3
Построим график функции ![]()
Сначала найдем точки пересечения графика функции с осями координат. Так как любая точка на оси ординат имеет абсциссу х = 0, то для этого значениях вычислим ![]() —точку A пересечения графика с осью ординат. Любая точка на оси абсцисс имеет ординату у = 0. Поэтому в формуле функции положим у = 0 и получим уравнение
—точку A пересечения графика с осью ординат. Любая точка на оси абсцисс имеет ординату у = 0. Поэтому в формуле функции положим у = 0 и получим уравнение ![]() Дробь равна нулю, если ее числитель 2х — 3 = 0 (а знаменатель при этом не равен нулю). Решив это уравнение, найдем х = 3/2 = 1,5 — точку В пересечения графика с осью абсцисс.
Дробь равна нулю, если ее числитель 2х — 3 = 0 (а знаменатель при этом не равен нулю). Решив это уравнение, найдем х = 3/2 = 1,5 — точку В пересечения графика с осью абсцисс.
Найдем теперь уравнения асимптот. Вертикальную асимптоту определим из условия, что данная функция не определена, т. е. знаменатель -х + 1 равен нулю, откуда х = 1. Горизонтальная асимптота находится из условия, что |х| велико. В этом случае для функции ![]() в числителе пренебрежем числом -3 (т. е. 2х - 3 ≈ 2х), в знаменателе пренебрежем числом 1 (т. е. -х + 1 ≈ -х). Тогда значение функции
в числителе пренебрежем числом -3 (т. е. 2х - 3 ≈ 2х), в знаменателе пренебрежем числом 1 (т. е. -х + 1 ≈ -х). Тогда значение функции ![]() Прямая у = -2 является горизонтальной асимптотой.
Прямая у = -2 является горизонтальной асимптотой.
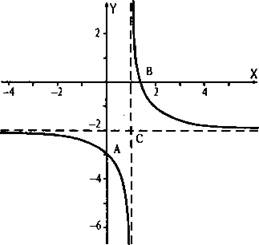
На координатной плоскости отметим точки А и В, построим асимптоты. Проведем ветви гиперболы, проходящие через точки А и В симметрично относительно точки С пересечения асимптот. При этом при х → 1 ветви графика приближаются к вертикальной асимптоте, при больших |х| ветви графика приближаются к горизонтальной асимптоте. Ветви графика при этом асимптоты не пересекают.
IV. Задание на уроке и дома
1. Постройте график функции:
![]()
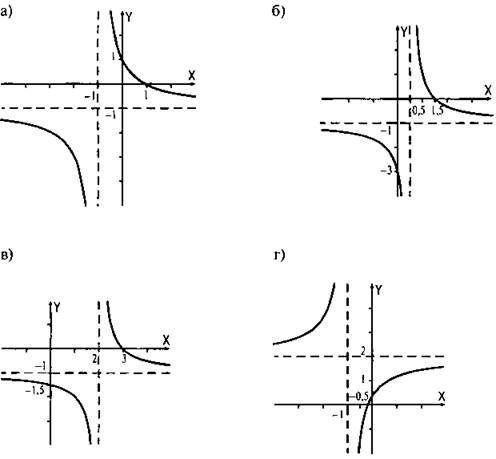
Ответы:
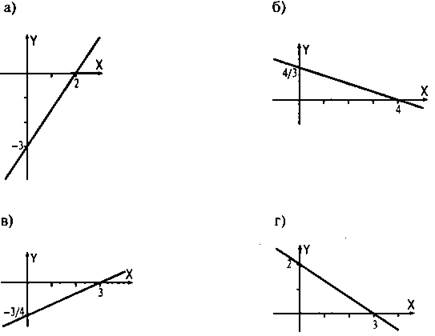
2. Постройте трафик функции:
![]()
Ответы:
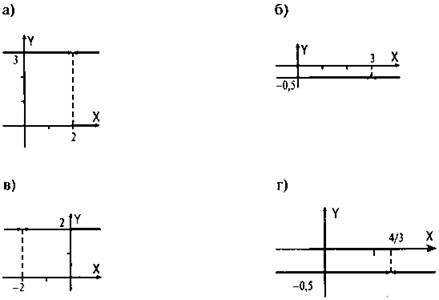
3. Постройте график функции:
![]()
Ответы:
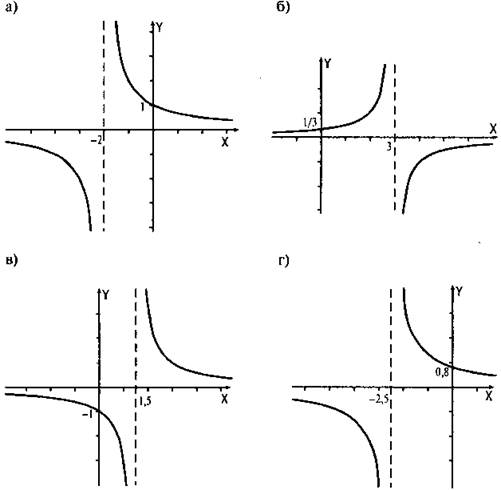
4. Постройте график функции:
![]()
Ответы:
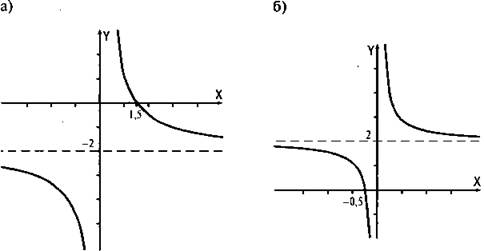
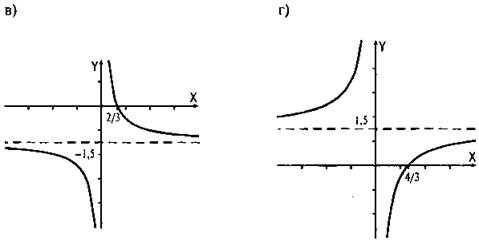
5. Постройте график функции:
![]()
Ответы: