Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Нахождение приближенных значений квадратного корня - ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА - КВАДРАТНЫЕ КОРНИ
Цель: приближенное вычисление квадратного корня.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Решите уравнение: а) х2 - 0,04 = 0,6; б) (2х - 3)2 = 16; в) (3х + а)2 = 81.
2. Определите число корней уравнения х2 - 4х = а.
Вариант 2
1. Решите уравнение: а) х2 + 0,05 = 0,3; б) (3х + 2)2 = 36; в) (2х - а)2 = 49.
2. Определите число корней уравнения -х2 + 6х = а.
III. Изучение нового материала (основные понятия)
Из предыдущих занятий известно, что ![]() может быть целым числом (например,
может быть целым числом (например, ![]() и т. д.), обыкновенной дробью (например,
и т. д.), обыкновенной дробью (например, 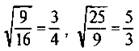 и т. д.), десятичной дробью (например,
и т. д.), десятичной дробью (например, ![]()
![]() и т. д.) и иррациональным числом (например,
и т. д.) и иррациональным числом (например, ![]() и т. д.). Так как иррациональное число является бесконечной десятичной непериодической дробью, то в практических вычислениях возникает вопрос о вычислении приближенного значения арифметического квадратного корня.
и т. д.). Так как иррациональное число является бесконечной десятичной непериодической дробью, то в практических вычислениях возникает вопрос о вычислении приближенного значения арифметического квадратного корня.
Пример 1
Найдем приближенное значение ![]() с двумя знаками после запятой. Оценим подкоренное выражение 3 сначала целыми числами. Так как 1 < 3 < 4, то
с двумя знаками после запятой. Оценим подкоренное выражение 3 сначала целыми числами. Так как 1 < 3 < 4, то ![]() или 1 <
или 1 < ![]() < 2. Поэтому десятичная запись числа
< 2. Поэтому десятичная запись числа ![]() начинается с цифры 1, т. е.
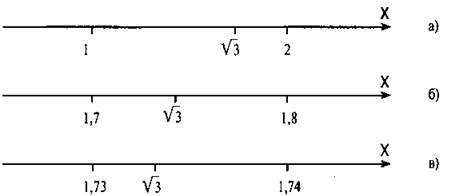
начинается с цифры 1, т. е. ![]() ≈ 1,... (рис. а).
≈ 1,... (рис. а).
Найдем теперь цифру десятых. Для этого будем возводить в квадрат десятичные дроби 1,1; 1,2; 1,3; ... до тех пор, пока вновь не оценим такими числами подкоренное выражение 3. Имеем: 1,12 = 1,21; 1,22 = 1,44; 1,32 = 1,69; 1,42 = 1,96; 1,52 = 2,25; 1,62 = 2,56; 1,72 = 2,89; 1,82 = 3,24. Так как 2,89 < 3 < 3,24 или 1,72 < 3 < 1,82, то 1,7 < ![]() < 1,8 . Значит,
< 1,8 . Значит, ![]() ≈ 1,7... . (рис. б).
≈ 1,7... . (рис. б).
Чтобы найти цифру сотых, будем последовательно возводить в квадрат десятичные дроби 1,71; 1,72; 1,73; ..., вновь оценивая подкоренное выражение 3. Имеем: 1,712 = 2,9241; 1,722 = 2,9584; 1,732 = 2,9929; 1,742 = 3,0276. Так как 1,732 < 3 < 1,742, то 1,73 < ![]() < 1,74 (рис. в). Поэтому
< 1,74 (рис. в). Поэтому ![]() ≈ 1,73.
≈ 1,73.
Аналогичным образом можно найти приближенное значение арифметического квадратного корня с любой заданной точностью.
В практических расчетах для нахождения приближенных значений квадратных корней используют специальные таблицы или вычислительную технику.
Пример 2
С помощью калькулятора найдем ![]() .
.
Введем в калькулятор число 27,4 и нажмем клавишу ![]() На экране появится число 5,234500931 — приближенное значение
На экране появится число 5,234500931 — приближенное значение ![]() . Полученный результат округляют до требуемого числа знаков. Округлим, например, этот результат до сотых и получим
. Полученный результат округляют до требуемого числа знаков. Округлим, например, этот результат до сотых и получим ![]() ≈ 5,23.
≈ 5,23.
IV. Задание на уроке
№ 323 (а, г); 324 (а); 325; 327 (а); 331 (а, в, д); 332 (а); 333 (а); 334 (а, в).
V. Задание на дом
№ 323 (б, д); 324 (б); 326; 327 (б); 328; 331 (б, г, е); 332 (б); 333 (б); 334 (б, г).
VI. Подведение итогов урока